贪心 + 构造
思路
神仙玩意,开始乱猜结论 + 乱搞得了 30 pts
然后看题解:
对于 $a_i$ ,如果 $k \mid a_i$ 就令 $a_i = 0$ ,否则为 $1$
引理 1:如果有解,必定是 $k \mid n$ 且 $n \ge k^2$ 且 $a_1 = a_n = 0$
引理 2:一定存在合法方案,使得原序列恰好划分为 $k$ 个子序列(证明考虑合并两个子序列后得到的序列仍然合法)
所以,我们就只考虑划分成 $k$ 个子序列的情况
引理 3:在引理 2 的情况下,一定存在方案使得前 $k$ 个 $0$ 是这 $k$ 个序列的左端点,后 $k$ 个 $0$ 是这 $k$ 个子序列的右端点
证明:
首先,如果有 $i < j$ 满足 $a_i = a_j = 0$ 且 $i$ 是某个子序列的右端点而 $j$ 是左端点,那么我们交换 $i, j$ ,让 $i$ 当原来 $j$ 所在子序列的左端点, $j$ 当原来 $i$ 所在子序列的右端点,其它数划分不变,一定仍然合法,所以一定有一种合法方案使得所有左端点一定在所有右端点前
然后,我们考虑左端点,如果存在 $i < j$ 满足 $a_i = a_j = 0$ 且 $i$ 不是端点而 $j$ 是左端点,由于所有左端点一定在所有右端点前,所以 $i \sim j$ 之间没有右端点,所以我们可以交换 $i, j$ ,让 $i$ 当左端点, $j$ 不当端点而去原来 $i$ 所在子序列中取代 $i$ 的位置,此时仍然合法;而对于所以右端点,可以同理
我们就只考虑满足引理 3 的情况
有了上面那么多引理,我们有个猜想
猜想 1:若存在合法方案,一定存在方案使得子序列之间不存在包含关系,即若 $l_1, r_1$ 是某个子序列的左/右端点, $l_2, r_2$ 是另一个子序列的左/右端点,不存在 $l_1 < l_2 < r_2 < r_1$
如果该猜想成立,我们就可以贪心求解
贪心 1:对于区间 $[l, r]$
- 若只有 $a_l, a_r$ 一对 $1$ ,直接把整个序列作为一个子序列
- 否则,设 $i$ 是左起第二个 $0$ 的位置, $[l, i]$ 之间一共有 $x$ 个 $1$ ,设 $y$ 是最小的满足 $(x + y) \equiv k - 2 \pmod k$ 的自然数, $j$ 是左起第 $x + y$ 个 $1$ 以后第一个 $0$ ,把 $l, j$ 以及那 $x + y$ 个 $1$ 作为一个子序列,然后递归处理剩下的数字,即区间 $[k, r]$ 去掉那 $y$ 个 $1$ 和 $j$
但讨厌的是,猜想 1 是假的,甚至样例都 hack 了:
1 | 0 |
我们来看看那里假了:
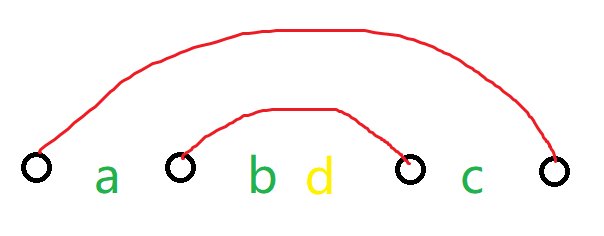
如图,有包含关系的两点子序列,现在两段子序列是 $a + b + c$ 和 $d$ (不含两端),我们要把它搞成:
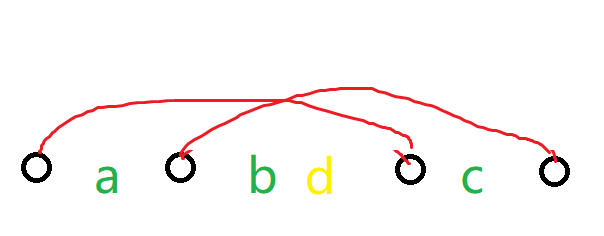
那么就要重新分配 $a, b, c, d$ ,显然 $a$ 的必须属于新的较左的序列,考虑用 $b + d$ 补齐为 $k$ 的倍数,但显然有可能不行
那么何时无法用 $b + d$ 补齐呢?显然是 $a + b + c > a + b + d$ ,即 $a > d$ 的时候,但是,由于 $d + 2 \equiv 0 \pmod k$ ,所以 $d$ 至少是 $k - 2$ ,这意味着 $a \equiv k - 1 \pmod k$ 且 $b = 0$ ,同理也可得 $c \equiv k - 1 \pmod k$
综上,猜想不成立当且仅当 $a, c \equiv k - 1 \pmod k$ 且 $b = 0$
那么我们继续猜想
猜想 2:必定存在合法方案使得 $a_1, a_n$ 在同一个子序列中
如果猜想成立,我们又有一个贪心(这就是我最开始打的 25 pts 的东西,然后乱搞特判得到 30 pts)
贪心 2:直接用引理 3 ,找到 $k$ 对端点,把所有都当成包含关系自外到内贪心分配
但是,显然也假(不然我为毛 25 pts),也是样例 hack 了:
1 | 0 |
我们还是来看为啥不对,设两个子序列端点为 $1, r_1$ $l_n, n$ ,由引理 3 显然 $1 < l_n < r_1 < n$ ,那么如果 $l_n$ 到 $r_1$ 之间有至少 $k - 2$ 个数,就可以通过调整使得 $1, n$ 和 $l_n, r_1$ 分别为新的两个子序列的端点,问题是在 $l_n$ 到 $r_1$ 之间不足的时候
然后神秘的东西就来了:
引理 4:若存在合法方案,一定要么猜想 1 成立,要么猜想 2 成立
别问,问就是“仔细思考,不难发现”
总之,只要把两个贪心拼一起即可
代码
咕了,现在不想码
看std吧