Dyd's Blog

He who has a strong enough why can bear almost any how.

广义SAM

Posted on Edited on In
Symbols count in article: 5.9k Reading time ≈ 5 mins.

多串的 SAM

广义SAM

SAM 是我们处理字符串问题最有效的工具之一，但它和很多工具一样有一个问题，那就是无法处理主串有多个的情况，于是我们就有了广义的 SAM

约定

  • 模式串为 $s_1, s_2, … s_n$ ，其长度和为 $m$

  • 将模式串建出的 Trie 为 $T$ ，其中节点个数为 $\mid T \mid$

  • $G(T)$ 表示 Trie 树中所有叶节点的深度和

不难证明，如果给定模式串集去构建 Trie ，则 $G(T) = O(m) = O(\mid T \mid)$ ；但如果直接给定一个 Tire ， $G(T) = \mid T \mid^2$

  • $A$ 为字符集

假广义 SAM

首先，网上流传着许多假的广义 SAM 写法，虽然它们是假的，但既然流传出来，说明还是有一定优势，那就是好打 + 好想（估计后者占主要），这里介绍几种：

  1. 把多个串用特殊符号连起来，然后再建 SAM

    优点是好想；缺点是你要加一些特判处理掉特殊符号，而且时间复杂度是 $O(m)$ 且常数好像很大（我没试过，但都说它危险）

  2. 每次插入一个串时把 $last$ 设为 $1$ ，再像普通 SAM 一样插入

    优点是好打（改两下就完了），且大部分时候可以保证正确性（比如 luogu 的板子题）；但缺点是会出现一些多余节点，有时候它们会影响答案，另外，时间是 $O(m)$ 但比 $1$ 快

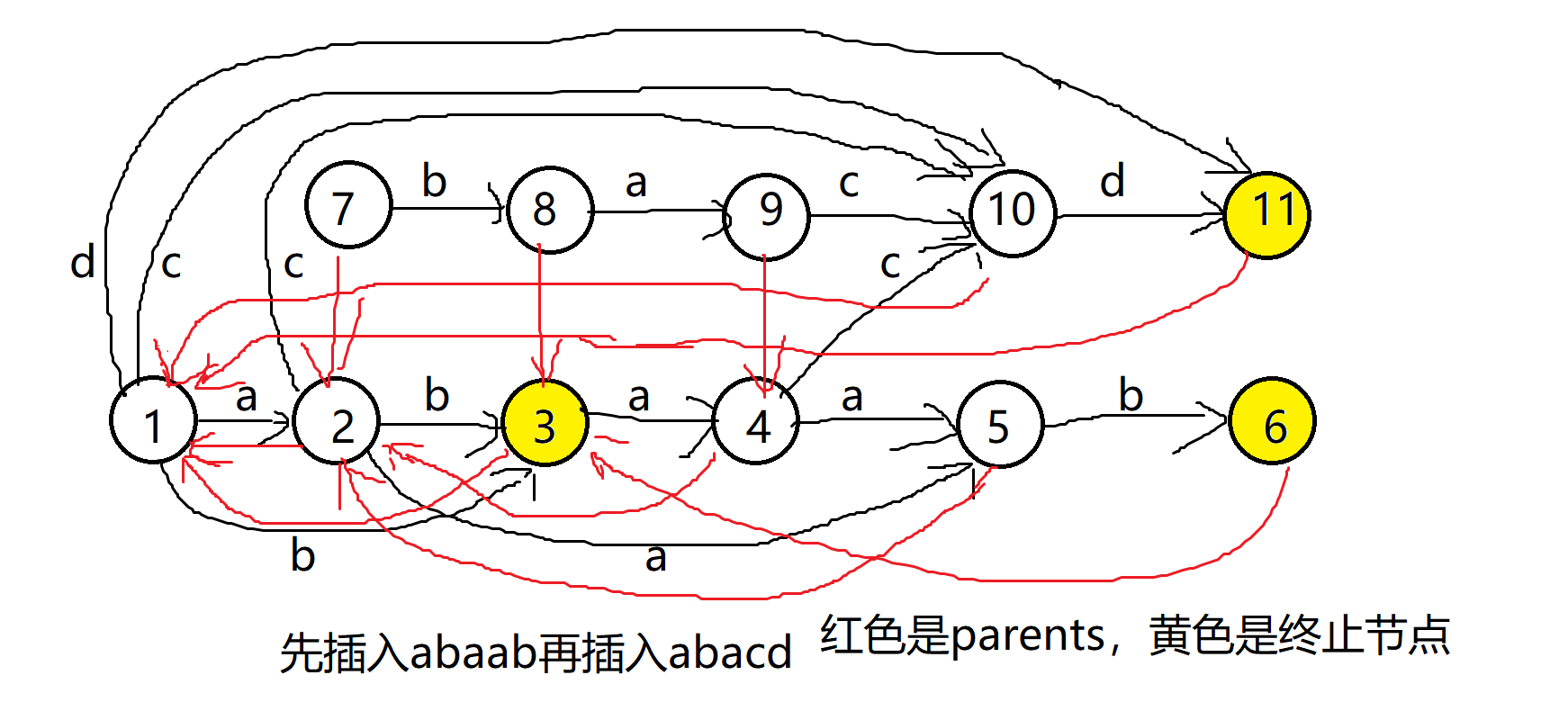    伪SAM（如图， $7, 8, 9$ 号节点是多余的)

其它还有一些，这里就不介绍了

离线版

我们都知道， SAM 的构造是在线的，这也是它的一个优势；而广义 SAM 也可以在线构造，不过在此之前，我们先学习离线构造方法

发现假广义 SAM $2$ 只是多了几个点，而多点的原因是 $aba$ 这个串被重复插入了，那么我们不妨先在一棵上 Trie 树把所有串插入，那么 Tire 树自然就帮我们合并了重复的部分，然后在 Tire 树上 dfs ，每次插入字符 $x$ 时，把 $last$ 设为 Trie 树上它的父节点对应 SAM 中节点即可，这其实就很像是假 SAM $2$ 的优化；发现 dfs 的时间是 $O(G(T))$ （因为你插入一个节点，它可能比前面的节点深度小，那你就要跳 parents 去修改）在出题人直接给出 Trie 树的时候时间为 $O(\mid T \mid^2)$ 很劣，我们把 dfs 换成 bfs ，时间保证为 $O(\mid T \mid) = O(m)$ ，而且在给定的串没有 lcp （也就是 Trie 建了个寂寞）的时候， bfs 写法可以避免很多特判

给出板子：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
#include <bits/stdc++.h>
using LL = long long;
const int N = 4e5 + 100, L = 1e6 + 100;
int n;
LL ans;
char s[L];
struct Trie
{
	int tot, c[L], fa[L], ch[L][26];
	Trie() : tot(1) {}
	void ins(char *s)
	{
		int p = 1;
		while (*s != '\0')
		{
			int t = *s++ - 'a';
			if (!ch[p][t]) ch[p][t] = ++tot, fa[tot] = p, c[tot] = t;
			p = ch[p][t];
		}
	}
} trie;
struct SAM
{
	struct Node{ int fa, len, ch[26]; } nd[L << 1];
	int& f(int x){ return nd[x].fa; }
	int& l(int x){ return nd[x].len; }
	int& c(int x, int y){ return nd[x].ch[y]; }
	int tot;
	SAM() : tot(1) {}
	int ins(int x, int las)
	{
		int p = las, cur = ++tot;
		l(cur) = l(p) + 1;
		while (p && !c(p, x)) c(p, x) = cur, p = f(p);
		if (!p) f(cur) = 1;
		else
		{
			int s = c(p, x);
			if (l(s) == l(p) + 1) f(cur) = s;
			else
			{
				int cl = ++tot;
				nd[cl] = nd[s], l(cl) = l(p) + 1;
				f(cur) = f(s) = cl;
				while (p && c(p, x) == s) c(p, x) = cl, p = f(p);
			}
		}
		return cur;
	}
	void bd()
	{
		std::queue<int> q;
		int pos[L];
		for (int i = 0; i < 26; ++i) if (trie.ch[1][i]) q.push(trie.ch[1][i]);
		pos[1] = 1;
		while (!q.empty())
		{
			int x = q.front(); q.pop();
			pos[x] = ins(trie.c[x], pos[trie.fa[x]]);
			for (int i = 0; i < 26; ++i) if (trie.ch[x][i]) q.push(trie.ch[x][i]);
		}
	}
} sam;
int main()
{
	scanf("%d", &n);
	while (n--) scanf("%s", s + 1), trie.ins(s + 1);
	sam.bd();
	ans = 0;
	for (int i = sam.tot; i > 1; --i) ans += sam.l(i) - sam.l(sam.f(i));
	printf("%lld\n", ans);
	return 0;
}

在线版

在线是 SAM 的一大优势，那如何把这个优势传承到广义 SAM 呢？

显然，我们建 Trie 的目的是压缩 lcp ，找到 last ，依次弥补假 SAM $2$ 的漏洞；其实还可以换个角度，还是每次插入一个串就把 last 设为 $1$ ，但加入一些特判，当 last 已经有这个儿子的时候我们特殊处理，不创建新节点，然后每次返回的下一个字符的 last ，就可以做到在线

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#include <bits/stdc++.h>
using LL = long long;
const int L = 1e6 + 100;
int n;
char s[L];
LL ans = 0;
struct SAM
{
	struct Node{ int len, fa, ch[26]; } nd[L << 1];
	int& l(int x){ return nd[x].len; }
	int& f(int x){ return nd[x].fa; }
	int& c(int x, int y){ return nd[x].ch[y]; }
	int tot;
	SAM() : tot(1) {}
	int ins(int x, int las)
	{
		if (c(las, x))
		{
			int p = las, s = c(p, x);
			if (l(s) == l(p) + 1) return s;
			else
			{
				int cl = ++tot;
				nd[cl] = nd[s], l(cl) = l(p) + 1;
				while (p && c(p, x) == s) c(p, x) = cl, p = f(p);
				f(s) = cl;
				return cl;
			}
		}
		int cur = ++tot, p = las;
		l(cur) = l(p) + 1;
		while (p && !c(p, x)) c(p, x) = cur, p = f(p);
		if (!p) f(cur) = 1;
		else
		{
			int s = c(p, x);
			if (l(s) == l(p) + 1) f(cur) = s;
			else
			{
				int cl = ++tot;
				nd[cl] = nd[s], l(cl) = l(p) + 1;
				while (p && c(p, x) == s) c(p, x) = cl, p = f(p);
				f(s) = f(cur) = cl;
			}
		}
		return cur;
	}
} sam;
int main()
{
	scanf("%d", &n);
	for (int i = 1; i <= n; ++i)
	{
		scanf("%s", s + 1);
		for (int j = 1, las = 1; s[j]; ++j) las = sam.ins(s[j] - 'a', las);
	}
	for (int i = sam.tot; i > 1; --i) ans += sam.l(i) - sam.l(sam.f(i));
	printf("%lld\n", ans);
	return 0;
}

时间复杂度分析

直接给出结论：

  • 状态数（节点数）为线性 $O(2 \mid T \mid)$
  • 转移函数（边数）上界为 $O(\mid T \mid \mid A\mid)$
  • 离线时间复杂度为 $O(\mid T \mid \mid A \mid + \mid T \mid)$
  • 在线时间复杂度为 $O(\mid T \mid \mid A \mid + G(T))$

不难发现，当给定模式串集的时候，离线和在线时间复杂度一样，实际运行时在线的常数明显更小，且好打，所以建议打在线；而当给定 Trie 的时候，离线的时间复杂度更优秀

例题

诸神眷顾的幻想乡

这题麻烦的地方在于树上的路径可以拐，发现如果是自上而下的路径我们就可做了，我们发现一个巧妙的性质：

对于无根树树上任意一条路径，一定可以找到一个叶节点使得以这个叶节点为根时，此路径是自上而下的

正确性显然，又看见本题保证叶子个数不超过 $20$ ，直接每个叶子为根都建出 Tire ，然后插到 SAM里面即可

考虑时间，如果我们用在线的办法，由于本题叶子节点只有 $20$ 个， $G(T)$ 其实和 $\mid T \mid$ 是一个级的（当然，如果你愿意，也可以去 dfs $20$ 次把 Trie 建出来）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
#include <bits/stdc++.h>
using LL = long long;
const int N = 1e5 + 100;
int n, num, c[N], h[N], idx, deg[N];
struct Edge{ int ne, ver; } e[N << 1];
LL ans = 0;
void add(int x, int y){ e[idx] = {h[x], y}, h[x] = idx++; }
struct SAM
{
	struct Ndoe{ int len, fa, ch[10]; } nd[(N * 20) << 1];
	int tot;
	SAM() : tot(1) {}
	int& l(int x){ return nd[x].len; }
	int& f(int x){ return nd[x].fa; }
	int& c(int x, int y){ return nd[x].ch[y]; }
	int ins(int x, int las)
	{
		if (c(las, x))
		{
			int p = las, s = c(p, x);
			if (l(s) == l(p) + 1) return s;
			int cl = ++tot;
			nd[cl] = nd[s], l(cl) = l(p) + 1;
			while (p && c(p, x) == s) c(p, x) = cl, p = f(p);
			return f(s) = cl;
		}
		int p = las, cur = ++tot;
		l(cur) = l(p) + 1;
		while (p && !c(p, x)) c(p, x) = cur, p = f(p);
		if (!p) f(cur) = 1;
		else
		{
			int s = c(p, x);
			if (l(s) == l(p) + 1) f(cur) = s;
			else
			{
				int cl = ++tot;
				nd[cl] = nd[s], l(cl) = l(p) + 1;
				while (p && c(p, x) == s) c(p, x) = cl, p = f(p);
				f(s) = f(cur) = cl; 
			}
		}
		return cur;
	}
} sam;
void dfs(int x, int fa, int las)
{
	int now = sam.ins(c[x], las);
	for (int i = h[x]; ~i; i = e[i].ne) if (e[i].ver != fa) dfs(e[i].ver, x, now);
}
int main()
{
	std::memset(h, -1, sizeof h), idx = 0;
	scanf("%d %d", &n, &num);
	for (int i = 1; i <= n; ++i) scanf("%d", c + i);
	for (int i = 1, u, v; i < n; ++i)
	{
		scanf("%d %d", &u, &v);
		add(u, v), add(v, u);
		++deg[u], ++deg[v];
	}
	for (int i = 1; i <= n; ++i) if (deg[i] == 1) dfs(i, -1, 1);
	for (int i = sam.tot; i > 1; --i) ans += sam.l(i) - sam.l(sam.f(i));
	printf("%lld\n", ans);
	return 0;
}