特殊图上的 NP-Hard 问题

弦图与区间图

考试的时候遇到了，就来看看，以下内容除代码外大部分来自 OIWiki 和 CDQ 的讲稿

定义

对于图 $G = (V, E)$

• 子图：若图 $G’ = (V’, E’)$ 满足 $E’ \subseteq E, V’ \subseteq V$ ，则称 $G’$ 为 $G$ 的子图
• 导出子图（诱导子图）：若$G$ 的一个子图 $G’ = (V’, E’)$ 满足 $\forall u, v \in V’, (u, v) \in E’$ 则称 $G’$ 为 $G$ 的一个导出子图
• 相邻点：与 $x$ 直接相连的点为其相邻点， $x$ 的相邻点集记作 $N(x)$
• 团：图的完全子图
• 极大团：不是其它任何团的子图的团
• 最大团：一个图的所有团中点数最多的一个；其点数记作 $\omega(G)$
• 最小染色：用最少的颜色给点染色使得所有边连接的两点颜色不同；其颜色数记作 $\chi(G)$
• 最大独立集：最大的点集使得点集中任意两点都没有边直接相连；该集合的大小记为 $\alpha(G)$
• 最小团覆盖：用最少的团覆盖所有的点；使用团的数量记为 $\kappa(G)$
• 弦：连接环中不相邻两点的边
• 弦图（三角化图）：任意长度大于 $3$ 的环都有一个弦的图称为弦图
• 点割集：对于图上两点 $u, v$ ，其点割集是 $V$ 的一个子集且满足删除点割集后 $u, v$ 不联通
• 极小点割集：该点割集的任意一个真子集都不是点割集

一些引理、定理、推论

Theorem1 ： $\omega(G) \le \chi(G)$ ：对最大团染色需要 $\omega(G)$ 种颜色

Theorem2 ： $\alpha(G) \le \kappa(G)$ ：每个团中最多选一个点进入最大独立集

Lemma1 ： 弦图的任意导出子图一定是弦图：导出子图的环必定来自原图

Corollary1 ：弦图的任意导出子图一定不可能是一个点数大于 $3$ 的环：同上

Lemma2 ：图关于 $u, v$ 的点割集将原图分成若干联通块，设包含 $u, v$ 的联通块分别为 $U, V$ ，对于 $u, v$ 的极小点割集中的任意一点 $x$ ，$N(x)$ 中一定包含 $U, V$ 中的点：若不包含，在极小点割集中删去 $x$ 也不会使 $U, V$ 联通

Theorem3 ：弦图上任意两点间的极小点割集的导出子图一定为一个团：

若点割集大小 $\le 1$ 显然成立

否则，任取 $x, y$ 属于点割集，由 Lemma2 知 $N(x)$ 中必有在 $U, V$ 中的点，设其为 $x_1, x_2$ ，类似设 $y_1, y_2$ （注意可能 $x_1 = y_1, x_2 = y_2$ ），由于 $U, V$ 为联通块，则原图上存在一个由 $x_1$ 到 $y_1$ 的最短路， $x_2$ 到 $y_2$ 的最短路， $x, y$ 构成的环 $x - x_1 \sim y_1 - y - y_2 \sim x_2 - y$ ，注意道这个环大小 $\ge 4$ ，根据弦图的定义，此时该环上一定存在一条弦，若这条弦连接了两个连通块，则点集不是点割集；若这条弦连接了单个连通块内部的两个点或一个连通块内部的一个点和一个点割集上的点，都不满足最短路的性质；所以这条弦只能连接 $x, y$

由此，可证弦图中每个极小点割集中的两点都有边直接相连，故引理得证

判定弦图

为了判定弦图，我们再引入两个定义：

• 单纯点：若 $N(x) + \{x\}$ 的导出子图为一个团，则称 $x$ 为一个单纯点
• 完美消除序列：令 $n = \mid V \mid$ ，完美消除序列为一个 $1 \sim n$ 的排列 $v_1, v_2, …, v_n$ 满足 $v_i$ 在 $\{v_i, v_{i + 1}, …, v_n\}$ 的导出子图中是单纯点

Theorem4 ：任何一个弦图都至少有一个单纯点，不是完全图的弦图至少有两个不相邻的单纯点

考虑数学归纳法，单独考虑每一连通块

当图与完全图同构时，图上任意一点都是单纯点；当图的点数 $\le 3$ 时，引理成立

若图的点数 $\le k$ 时成立，现在证明点数 $ = k$ 时成立：若图不为完全图，必有 $(u, v) \notin E$ ，设 $I$ 是 $u, v$ 的极小点割集， $A, B$ 分别是删去 $I$ 后 $u, v$ 所在联通块，因为 $A$ 是原图的导出子图，结合 Lemma1 可知 $A$ 一定是弦图且点数 $< k$ ，所以 $A$ 中至少有一个单纯点，设 $L = A + I$ ，若 $L$ 为完全图， $u$ 为原图的单纯点；否则，同样因为 $L$ 是原图的导出子图，一定是弦图且点数 $< k$ ，所以有两个不相邻的单纯点，由 Theorem4 知 $I$ 是一个团，所以 $A$ 中那个单纯点在原图中也是单纯点；综上 $A$ 中至少包含原图的一个单纯点，同理可得 $B$ 中也包含一个单纯点，由数学归纳法原理，引理得证

Theorem5 ：一个无向图是弦图的充要条件是它有一个完美消除序列

充分性：对于点数为 $n$ 的弦图，取其一个单纯点为 $v_n$ ，删去该点，由 Lemma1 知图变成一张点数为 $n - 1$ 的弦图，依次递归下去可得弦图的完美消除序列

必要性：假设有无向图存在结点数 $> 3$ 的环且拥有完美消除序列，设在完美消除序列中出现的第一个环上的点为 $v$ ，设 $v$ 在环上与 $v_1, v_2$ 相连，则由完美消除序列的性质即单纯点的定义可得 $v_1, v_2$ 直接有边相连，矛盾

MCS 算法

直接求完美消除序列显然不行，一般有字典序广度优先搜索算法（ Lexicographic BFS, LexBFS ）和最大势算法（ Maximum Cardinality Search, MCS ），两者都是 $O(n + m)$ 的，这里介绍后者

MCS 的思想就是倒着从 $n$ 到 $1$ 给节点标号，记录 $label[i]$ 表示第 $i$ 个点和多少个已经标号的点相邻，每次取 $label[i]$ 最大的未标号节点标号

正确性证明：

设 $pos(x)$ 表示点 $x$ MCS 算法求得的序列中的位置

Lemma3 ：任意一个弦图一定不存在一个序列 $v_0, v_1, …, v_k(k \ge 2)$ 满足：

1. $v_i, v_j$ 相连当且仅当 $\mid i - j \mid = 1$
2. $pos(v_0) > pos(v_i) (i \in [1, k])$
3. 存在 $x \in [1, k - 1]$ ，满足 $pos(v_x) < pos(v_{x + 1}) < … < pos(v_k)$ 且 $pos(v_x) < pos(v_{x - 1}) < … < pos(v_1) < pos(v_k) < pos(v_0)$

由于 $pos(v_1) < pos(v_k) < pos(v_0)$ 且 $v_1, v_0$ 相连， $v_k, v_0$ 不相连，所以必然存在 $y$ 不属于该序列使得 $pos(v_k) < pos(y)$ 且 $v_k, y$ 相连， $v_1, y$ 不相连（这样才能使 $pos(v_1) < pos(v_k)$ ）

考虑最小的 $j \in [2, k]$ 满足 $v_j, y$ 相连，若 $v_0, y$ 相连，则 $v_0, v_1, …, v_j, x$ 构成一个长度 $\ge 4$ 且无弦的环，于弦图的定义矛盾，所以 $v_0, y$ 不相连

若 $pos(y) < pos(v_0)$ ，则 $v_0, v_1, …, v_j, y$ 也是一个满足定义的序列；若 $pos(y) > pos(v_0)$ ，则 $y, v_j, …, v_1, v_0$ 也是一个满足性质的序列；无论如何，新序列的 $\min(pos(v_0), pos(v_k))$ 都变大了，这个过程可以无限进行下去，但 $pos()$ 的最大值是有限的 $n$ ，所以矛盾

Theorem6 ：对于任何一个弦图， MCS 算法求出的序列一定是一个完美消除序列

考虑任意三个点 $u, v, w$ 满足 $pos(u) < pos(v) < pos(w)$ ，如果 $u, v$ 相连，$u, w$ 相连，且 $v, w$ 不相连的话， $w, u, v$ 构成一个 Lemma3 中的序列，这显然是矛盾的，所以如果 $u, v$ 相连，$u, w$ 相连，则 $v, w$ 必定相连，再加上这是一张弦图，必定存在完美消除序列，则定理得证

时间复杂度分析：

拿一个懒惰删除的链表记录 $label[i] = x$ 的点有多少个，每条边扫到的时候会向链表中插入一个点，所以复杂度是 $O(n + m)$ 的

回归正题：判定弦图

我们对一个图做了 MCS ，得到一个序列，如何判定这是不是完美消除序列呢？

直接暴力就算依次判定 $v_i$ 和 $\{v_i, v_{i + 1}, …, v_n\} \cap N(v_i)$ 是否构成团，这是 $O(nm)$ 的，实际上，把 $\{v_i, v_{i + 1}, …, v_n\} \cap N(v_i)$ 从小到大排成 $\{v_{c_1}, v_{c_2}, …, v_{c_k}\}$ ，只要判断 $v_{c_1}$ 与其它点是否直接联通即可，每个点/边只会扫一遍，时间 $O(n + m)$

综上，我们用 MCS 算法在 $O(n + m)$ 的时间解决了判定弦图的问题

而以下讨论均视做已经用 MCS 求出完美消除序列

弦图的极大团

Theorem7 ：令 $N’(x)$ 为满足与 $x$ 直接有边相连且在完美消除序列上的位置在 $x$ 之后的点的集合，则弦图的极大团一定可以写作 $\{x\} + N’(x)$ ，其中 $x$ 是该团在完美消除序列中第一次出现；正确性显然

Corollary2 ：弦图最多有 $n$ 个极大团

现在求极大团就转换为判定 $\{x\} + N’(x)$ 是否为极大团，对于 $A = \{x\} + N’(x), B = \{y\} + N’(y)$ ，若 $A \subseteq B$ 则 $A$ 不是极大团，那么显然 $pos(y) < pos(x)$ ，设 $ne(v)$ 表示 $N’(v)$ 中 $pos$ 最小的点， $z$ 是满足 $y = z$ 时 $A \subseteq B$ 的最后一个点，那么 $ne(z) = x$ （否则 $y = ne(z)$ 时仍然有 $A \subseteq B$ ），而且 $A \subseteq B$ 当且仅当 $\mid A \mid + 1 \le \mid B \mid$

那么只需对于每个 $x$ ，判断是否存在一个 $y$ ，满足 $ne(x) = y$ 且 $\mid A \mid + 1 \le \mid B \mid$ 即可， $O(n + m)$

弦图的最大团/最小染色

最大团比极大团好做的多，枚举每个点，取 $\{x\} + N’(x)$ 最大的即可， $O(n)$

由 Theorem1 得最小染色数大于最大团大小，下面给出构造方案：按完美消除序列从后往前依次给每个点染色，给每个点染上可以染的最小颜色，这样构造的最小染色数就是最大团大小

弦图的最大独立集/最小团覆盖

最大独立集：完美消除序列从前往后，贪心选择所有没有与已经选择的点有直接连边的点

最小团覆盖：上面所求的最大独立集中每个元素 $x$ 对应的团 $\{x\} + N’(x)$ 即为最小团覆盖中的一个团，这样构造出的最小团覆盖就等于最大独立集大小，由 Theorem2 可知其最小

MCS 算法的代码实现

namespace MCS
{
	std::vector<int> cnt[N];
	bool vis[N];
	int pos[N], label[N], order[N], ne[N], N_[N];
	int stk[N], top;
	void init(int n)
	{
		for (int i = 1; i <= n; ++i) cnt[i].clear();
		std::memset(vis, false, (n + 1) * sizeof(bool));
		std::memset(pos, 0, (n + 1) << 2);
		std::memset(label, 0, (n + 1) << 2);
		std::memset(order, 0, (n + 1) << 2);
	}
	void mcs()
	{
		for (int i = 1; i <= n; ++i) cnt[0].pb(i);
		int mxct = 0, x = 0;
		for (int i = n; i; --i)
		{
			x = 0;
			while (mxct >= 0)
			{
				for (int j = cnt[mxct].size() - 1; ~j; --j)
					if (vis[cnt[mxct][j]]) cnt[mxct].pop_back();
					else{ x = cnt[mxct][j]; break; }
				if (!x) --mxct;
				else break;
			}
			vis[x] = true;
			order[i] = x, pos[x] = i;
			for (int j = h[x], y; ~j; j = e[j].ne) if (!vis[y = e[j].ver])
			{
				cnt[++label[y]].pb(y);
				mxct = std::max(mxct, label[y]);
			}
		}
	}
	bool judge() //判断是否是弦图
	{
		std::memset(vis, false, (n + 1) * sizeof(bool));
		for (int i = n, ct; i; --i)
		{
			top = 0, ct = 1;
			for (int j = h[order[i]]; ~j; j = e[j].ne) if (pos[e[j].ver] > i)
			{
				vis[stk[++top] = e[j].ver] = true;
				if (pos[stk[top]] < pos[stk[1]]) std::swap(stk[top], stk[1]);
			}
			for (int j = h[stk[1]], y; ~j; j = e[j].ne) if (vis[y = e[j].ver] && y != stk[1]) ++ct;
			if (top && ct != top) return false;
			while (top) vis[stk[top--]] = false;
		}
		return true;
	}
	int _max_clique() //极大团个数
	{
		int res = 0;
		for (int i = 1, x; i <= n; ++i)
		{
			top = 0;
			for (int j = h[order[i]], y; ~j; j = e[j].ne) if (pos[y = e[j].ver] > i)
			{
				stk[++top] = y;
				if (pos[stk[top]] < pos[stk[1]]) std::swap(stk[top], stk[1]);
			}
			ne[order[i]] = stk[1];
			N_[order[i]] = top;
		}
		for (int i = 1; i <= n; ++i)
		{
			if (!vis[order[i]]) ++res;
			if (N_[order[i]] >= N_[ne[order[i]]] + 1) vis[ne[order[i]]] = true;
		}
	}
	int max_clique() //最大团/最小着色
	{
		int res = 0;
		for (int i = 1; i <= n; ++i) res = std::max(res, label[i] + 1);
		return res;
	}
	int max_independent_set() //最大独立集/最小团覆盖
	{
		std::memset(vis, false, (n + 1) * sizeof(bool));
		int res = 0;
		for (int i = 1; i <= n; ++i) if (!vis[order[i]])
		{
			++res;
			vis[order[i]] = true;
			for (int j = h[order[i]]; ~j; j = e[j].ne) vis[e[j].ver] = true;
		}
		return res;
	}
}

完美图与伴完美图

CDQ 的 ppt 只讲了定义

• 完美图：一个图称完美图，当且仅当它的所有导出子图都满足 $\omega(G) = \chi(G)$
• 伴完美图：一个图称伴完美图，当且仅当它的每一个导出子图都满足 $\alpha(G) = \kappa(G)$

Theorem8 ：完美图 = 伴完美图（那定义个寄啊）

弦图是完美图的一种

区间图

• 区间图：给定一些区间，在一张图上每个点代表一个区间，两点间有边当且仅当对应两区间有交，则称此图为区间图

Theorem9 ：区间图一定是弦图

若区间图中存在一个长度 $> 3$ 的无弦环，对应在区间里面就有 $k > 3$ 个区间，它们依次有交点，而最后一个区间必须要和第一个区间相交才能构成环，这就意味着它会与中间的区间相交，这与该环无弦矛盾

值得注意的是 Theorem9 只对线型的区间成立，如果是圆环上的一些区间的话，它们是可以构成长度 $> 3$ 的无弦环的

区间图的判断要用到 PQ Tree 非常复杂，这里略过

极大团树

不知道有啥用的树

• 极大团树：定义一个图的极大团树 $T$ 为： $T$ 的顶点为 $G$ 所有极大团，对于每个点，包含它的的所有极大团为 $T$ 的一个联通子图

嫖一张 ppt 上的图：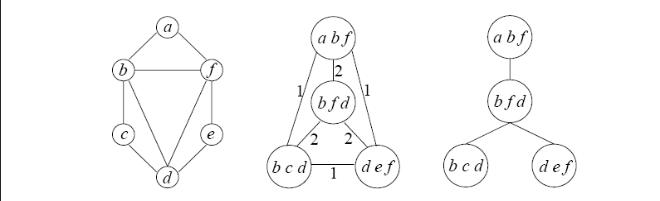

Theorem10 ：一个图为弦图的充要条件是它存在一棵极大团树；一个图为区间图的充要条件是它存在一棵极大团树是一条链

顺便， ppt 上的图也给出了极大团树的构建方法：

1. 找出弦图的所有极大团
2. 构建图 $G’$ ：极大团为点，两点之间边权为两个极大团的交集中的点的个数
3. 求 $G’$ 的一棵最大生成树