Dyd's Blog

He who has a strong enough why can bear almost any how.

luoguP7916 [CSP-S 2021] 交通规划

Posted on In
Symbols count in article: 6.3k Reading time ≈ 6 mins.

最小割的部分分应该可拿

交通规划

最小割

考虑网络流，把一条异色边看作被割掉，最后目标是让黑、白点不联通，显然的最小割，每次重新建图跑网络流即可，可得 $65/70/60pts$ （ luogu/loj/uoj ）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
#include <bits/stdc++.h>
using LL = long long;
const int N = 500 + 50, K = 50 + 5, INF = 0x3f3f3f3f;
int n, m, S, T, tot, num;
struct Edge{ int ne, ver, w; } eb[(N * N) << 2], e[(N * N) << 2];
int hb[N * N], idb = 0, h[N * N], idx = 0;
int q[N * N], hh, tt;
int dep[N * N], cur[N * N];
int id(int x, int y){ return (x - 1) * m + y; }
void add(int x, int y, int z){ eb[idb] = {hb[x], y, z}, hb[x] = idb++; }
void dad(int x, int y, int z){ add(x, y, z), add(y, x, z); }
void add2(int x, int y, int z){ e[idx] = {h[x], y, z}, h[x] = idx++; }
void dad2(int x, int y, int z){ add2(x, y, z), add2(y, x, z); }
bool bfs()
{
	std::memset(dep, 0, sizeof dep);
	q[hh = tt = 1] = S, cur[S] = h[S], dep[S] = 1;
	for (int x; hh <= tt; )
	{
		x = q[hh++];
		for (int i = h[x], y; ~i; i = e[i].ne) if (e[i].w && !dep[y = e[i].ver])
		{
			dep[y] = dep[x] + 1, cur[y] = h[y];
			if (y == T) return true;
			q[++tt] = y;
		}
	}
	return false;
}
int find(int x, int lim)
{
	if (x == T) return lim;
	int flow = 0, t;
	for (int i = cur[x], y; ~i && flow < lim; i = e[i].ne)
	{
		cur[x] = i;
		if (e[i].w && dep[y = e[i].ver] == dep[x] + 1)
		{
			t = find(y, std::min(lim - flow, e[i].w));
			if (!t) dep[y] = -1;
			else e[i].w -= t, e[i ^ 1].w += t, flow += t;
		}
	}
	return flow;
}
LL dinic()
{
	LL res = 0;
	int flow;
	while (bfs())
		while (flow = find(S, INF)) res += flow;
	return res;
}
int main()
{
	scanf("%d %d %d",&n, &m, &num);
	std::memset(hb, -1, sizeof hb);
	std::memset(h, -1, sizeof h);
	for (int i = 1, w; i < n; ++i)
		for (int j = 1; j <= m; ++j)
		{
			scanf("%d", &w);
			dad(id(i, j), id(i + 1, j), w);
		}
	for (int i = 1, w; i <= n; ++i)
		for (int j = 1; j < m; ++j)
		{
			scanf("%d", &w);
			dad(id(i, j), id(i, j + 1), w);
		}
	S = id(n, m) + 1, tot = T = S + 1;
	for (int k, w, p, col; num--; )
	{
		scanf("%d", &k);
		std::copy(hb + 1, hb + tot + 1, h + 1);
		std::copy(eb, eb + idb, e);
		idx = idb, tot = T;
		for (int i = 1; i <= k; ++i)
		{
			scanf("%d %d %d", &w, &p, &col);
			++tot;
			col ? dad2(S, tot, INF) : dad2(tot, T, INF);
			if (p <= m) dad2(id(1, p), tot, w);
			else if (p <= m + n) dad2(id(p - m, m), tot, w);
			else if (p <= (m << 1) + n) dad2(id(n, m - (p - m - n) + 1), tot, w);
			else dad2(id(n - (p - m - m - n) + 1, 1), tot, w);
		}
		printf("%lld\n", dinic());
	}
	return 0;
}

正解

竟然是对偶图最短路 + 区间dp ，简直了

只有两个附加点

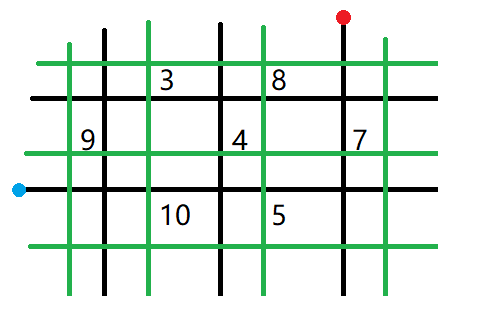先考虑 $k = 2$ 且异色的情况（就是样例 $1$ ，为了方便用红/蓝代替黑/白点）：对偶图如图，黑色是原图，绿色是对偶图，绿色边的边权等于它穿过的黑色边的边权，我们让红、蓝点不联通的过k程其实就对应着在绿色图上找一个分界线使红、蓝点在分界线两边

那怎么找呢？我们在红、蓝点连线两侧创建起点和终点（称它们为关键点），分别向对应的对偶图（绿）的边界上的节点连权为 $0$ 的边，跑最短路即可

多个附加点

那如果有多个附加点怎么办？首先我们明确的一点是，如果两个同色的附加点相邻，我们可以把它们合并，当做一个点

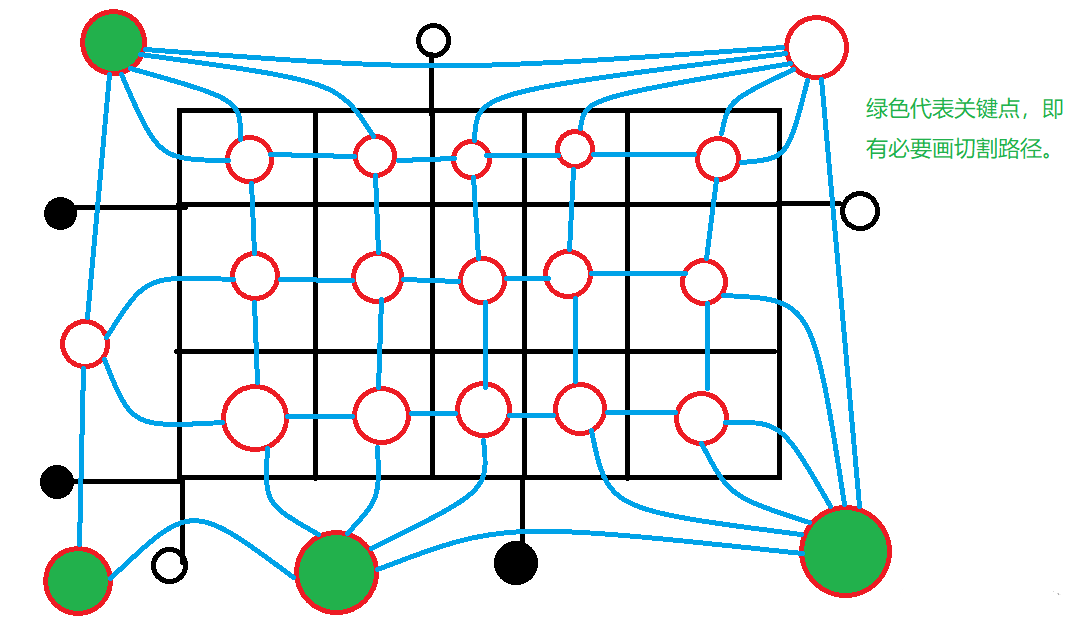但好像点的数量还是 $O(k)$ 的，类比上面只有两个点的情况，我们发现其实还是要在对偶图上找一些分界线使得异色的附加点被分隔开；我们不妨先找到关键点，不难发现关键点与附加点应该相间排布（这样才能保证关键点在异色附加点连线的两边），且关键点于和自己直接相邻的对偶图中节点相连，嫖一张图：关键点易得关键点数量是 $O(k)$ 级的，感觉好像还是没啥区别；不管，我们先考虑如何找到一组合法的分界线，结论是：任意将绿色的点两两配对求最短路即可得到一组合法的分界线，正确性其实比较显然，考虑一对异色点被分隔开的充要条件是存在处于它们异侧的关键点的路径即得

关键点不多，两两之间的最短路径可以直接上 dijkstra ，但 $O(k)$ 的数量级如果要枚举两两如何配对的话就太大了，手玩一下 然后瞟题解 可知，最后的配对方案中路径一定是不交也不重的（如果有两条路径相交/重，那么交换一对关键点不会使答案变差），这意味着顺时针四个关键点 $1, 2, 3, 4$ 不会存在 $(1, 3), (2, 4)$ 的配对，这就变成很简单的括号匹配，区间 dp 可以做到 $O(k^3)$

综上，总时间为 $O(\sum k^3 + \sum k * nm \log nm)$

代码

难点在构图，标号不好处理，注意就算是同色的附加点之间的部分也应该在对偶图中对应一个点，否则最短路会求错；另外，为了方便，我把所有区间都建了点，从中选关键点来跑最短路（加上大量使用 STL 导致常数巨大）；注意环形 dp 要倍长，且发现只有偶数长度有意义（两两配对）；最后，注意特判答案为 $0$ （不存在关键点）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
#include <bits/stdc++.h>
#define fi first
#define se second
using LL = long long;
const int N = 500 + 50, K = 50 + 5;
int n, m, T, tot, a[K];
struct Edge{ int ne, ver, w; } e[(N * N) << 2];
int h[N * N], idx, toe[N][N][2]; //[0]:(i,j)->(i,j-1),[1]:(i,j)->(i-1,j)
std::pair<int, int> nd[K];
std::bitset<N * N> vis;
std::priority_queue< std::pair<int, int> > q;
LL d[K << 1][K << 1], ds[K << 1][K << 1],  dis[N * N];
void add(int x, int y, int z){ e[idx] = {h[x], y, z}, h[x] = idx++; }
void dad(int x, int y, int z){ add(x, y, z), add(y, x, z); }
int id(int x, int y){ return x * (m + 1) + y + 1; } //返回(x,y)右下对于区域的编号
void cg(int p, int w)
{
	int t;
	if (p <= m) t = toe[0][p][0];
	else if (p <= m + n) t = toe[p - m][m][1];
	else if (p <= m * 2 + n) t = toe[n][m - (p - m - n) + 1][0];
	else t = toe[n - (p - m * 2 - n) + 1][0][1];
	e[t].w = e[t ^ 1].w = w;
}
int find(int p)
{
	if (p <= m) return id(0, p);
	else if (p <= m + n) return id(p - m, m);
	else if (p <= m * 2 + n) return id(n, m - (p - m - n) + 1 - 1);
	else return id(n - (p - m * 2 - n) + 1 - 1, 0);
}
void dij(int st)
{
	std::memset(dis, 0x3f, sizeof dis), vis.reset();
	dis[st] = 0, q.push({0, st});
	while (!q.empty())
	{
		int x = q.top().se; q.pop();
		if (vis[x]) continue;
		vis[x] = 1;
		for (int i = h[x], y; ~i; i = e[i].ne) if (!vis[y = e[i].ver] && dis[y] > dis[x] + e[i].w)
		{
			dis[y] = dis[x] + e[i].w;
			q.push({-dis[y], y});
		}
	}
}
LL dp()
{
	std::memset(d, 0x3f, sizeof d);
	LL res = d[0][0];
	for (int i = 1; i <= tot; ++i)
		for (int j = 1; j <= tot; ++j) ds[i + tot][j] = ds[i][j + tot] = ds[i][j];
	for (int i = (tot << 1) - 1; i; --i) d[i][i + 1] = ds[i][i + 1];
	for (int len = 4; len <= tot; len += 2)
		for (int l = 1, r = l + len - 1; l <= tot; ++l, ++r)
		{
			d[l][r] = d[l + 1][r - 1] + ds[l][r];
			for (int k = l + 1; k < r; ++k) d[l][r] = std::min(d[l][r], d[l][k] + d[k + 1][r]);
		}
	for (int i = 1; i <= tot; ++i) res = std::min(res, d[i][i + tot - 1]);
	return res;
}
int main()
{
	std::memset(h, -1, sizeof h), idx = 0;
	scanf("%d %d %d", &n, &m, &T);
	for (int i = 1, w; i < n; ++i)
		for (int j = 1; j <= m; ++j)
		{
			scanf("%d", &w);
			toe[i][j][0] = idx, dad(id(i, j), id(i, j - 1), w);
		}
	for (int i = 1, w; i <= n; ++i)
		for (int j = 1; j < m; ++j)
		{
			scanf("%d", &w);
			toe[i][j][1] = idx, dad(id(i, j), id(i - 1, j), w);
		}
	for (int i = 1; i <= m; ++i)
	{
		toe[0][i][0] = idx;
		dad(id(0, i), id(0, i - 1), 0);
		toe[n][i][0] = idx;
		dad(id(n, i), id(n, i - 1), 0);
	}
	for (int i = 1; i <= n; ++i)
	{
		toe[i][0][1] = idx, dad(id(i, 0), id(i - 1, 0), 0);
		toe[i][m][1] = idx, dad(id(i, m), id(i - 1, m), 0);
	}
	for (int k, w, p, t; T--; )
	{
		scanf("%d", &k);
		for (int i = 1; i <= k; ++i)
		{
			scanf("%d %d %d", &w, &p, &t);
			cg(p, w), nd[i] = {p, t};
		}
		std::sort(nd + 1, nd + k + 1);
		nd[k + 1] = nd[1], tot = 0;
		for (int i = 1; i <= k; ++i) if (nd[i].se != nd[i + 1].se) a[++tot] = find(nd[i].fi);
		if (!tot){ puts("0"); goto E_O_F_T; }
		std::memset(ds, 0x3f, sizeof ds);
		for (int i = 1; i <= tot; ++i)
		{
			dij(a[i]);
			for (int j = i + 1; j <= tot; ++j) ds[i][j] = ds[j][i] = dis[a[j]];
		}
		printf("%lld\n", dp());
		E_O_F_T: for (int i = 1; i <= k; ++i) cg(nd[i].fi, 0);
	}
	return 0;
}