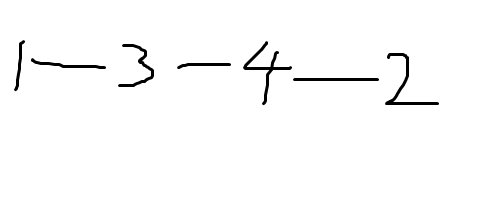Dyd's Blog

He who has a strong enough why can bear almost any how.

ARC142

Posted on Edited on In
Symbols count in article: 7.4k Reading time ≈ 7 mins.

蒟蒻的第二次 ARC

link

result

res

只能说我太弱了（差一点就掉 rating），但有幸和 tourist 打同场还是比较开心，发现那些人手速都好快啊，有个人和我做的题一样，但 19:12 就打完了（此时我一道题都还没做）

During

一进去， A 题比我想象的难（虽然其实很简单），思路大概就是把这个数和反过来的数分别加 $0$ 直到比 $n$ 大，但几个细节都没想清楚， WA 了三发就去看 B 了

B 感觉比 A 简单，因为发现只有周围是 $8$ 个全满的才有可能不满足（其它位置周围都是奇数），看样例就发现只要上一行比下一行大，然后本行中一大一小交替即可

AC 了 B 以后同机房有人过了 A ，他告诉我如果原数 $x$ 反转后 $x’ < x$ 就没有方案，因为原题中那个函数定义的是最小的，我仔细一看好像是的，就判了一下，结果还是 WA ，就一边问一边看 C ，在 C 有个大概思路的时候发现了 A 的问题：我求原数反转求错了！直接改掉过了 A （吃了 $5$ 发罚时我也是醉了）

C 我的大概思路就是直接问每个点到 $1, 2$ 的距离，如果 $1, 2$ 没有直接相连那答案就是 $\min(dis(u, 1) + dis(u, 2))$ ；如果每个 $u$ 都满足 $\mid dis(u, 1) - dis(u, 2) \mid == 1$ 我就认为 $1, 2$ 直接相连，因为 A 的罚时有点多， 我没多想就交了，一看， WA 一个点！蒙都知道是 $1, 2$ 直接相连判断错了，然后仔细一想，自己 hack 了自己：hack

上图的情况下我的思路会判断成 $1, 2$ 直接相连，并且发现能 hack 我的情况只有上面那个 $1, 2$ 中间两个点（那两个点上可能还有点），并且由于我上面只问了 $2n - 4$ 次，就直接找到这两个点，然后问它们的距离，如果为 $1$ 就是 hack 的情况，输出 $3$ ，最离谱的是期间因为交互题没 fflush(stdout) TLE 了两发（血亏），不管怎样终于 AC 了

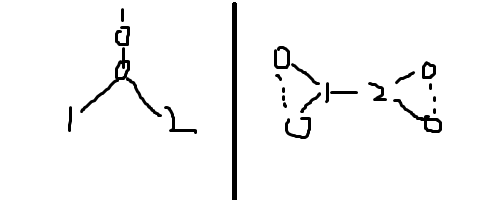
这里同机房的 l18q 巨佬有个很好的思路： $\mid dis(u, 1) - dis(u, 2) \mid$ 和 $dis(u, 1) + dis(u, 2)$ 中必有一个是 $1, 2$ 之间的距离，所以他也询问 $2n - 4$ 次，统计次数，出现恰好一半的就是答案，但特殊情况有两个，他只考虑到了前者，所以考场上挂的有点多：hack2

上面就是两种特殊情况，第一种直接判断如果有点 $dis(u, 1) == dis(u, 2)$ 那答案就是两个相加；第二种有点麻烦，因为统计出来距离为 $1, 2$ 各占一半，解决方法就是随便取两个相对点问一下距离，如果是 $3$ 答案就是 $1$

搞完 C 去看了一眼榜， 第一不是 tourist 把我惊呆了 ，发现大部分人都过了 ABC 在搞 DEF ，感觉搞出一道排名就会很好看 这不废话 ，虽然 D 过的人多，但我感觉没看懂题就去看 E ，想了半天决定贪心 + 退火乱搞，几乎卡着时间打（开打的时候只有 $20min$ 了）完改了几次参数没退过去

After

隔了一天来改题

D

认真读了下题，理清了题意，有点后悔考场上去打 E ，但也就一点点，因为这题也好难啊

首先考虑可以进行无限多次操作，我们考虑一条路径，它的所有顶点中只有一个端点上没有棋子，那么显然这些棋子可以在该路径上一直来回，无限多次的条件就被满足了，但唯一性还没满足，不唯一显然是一个路径上有点走到外面去了，那么该路径有棋子的某个点连向某条路径有棋子的端点（这样那个端点走后就给这个点留出位置）

于是考虑树形 dp 求出将树划分成若干条上述路径的方案数，显然这就是答案，问题在于状态和转移，我们称有棋子的端点为“占”，无其中的端点为“空”，发现一共有 $5$ 中情况：

  • 该点所在路径的占在上面，空在该点或其子树内
  • 该点所在路径的空在上面，占在该点或其子树内
  • 该点就是占，空在子树内
  • 该点就是空，占在子树内
  • 占、空都在子树内

那么设其为 $d[x, 0/1/2/3/4]$ ，显然转移为 $y$ 是 $x$ 的儿子， $y’, y’’$ 是任意一个 $y$ ：
$$
\begin{aligned}
& d[x, 0] += \prod d[y, 2] \\
& d[x, 0] += d[y’, 0] * \prod d[y, 4] \\
& d[x, 1] += \prod d[y, 3] \\
& d[x, 1] += d[y’, 1] * \prod d[y, 4] \\
& d[x, 2] += d[y’, 0] * \prod d[y, 3] \\
& d[x, 3] += d[y’, 1] * \prod d[y, 2] \\
& d[x, 4] += d[y’, 0] * d[y’, 1] * \prod d[y, 4] \\
\end{aligned}
$$
发现 $1$ 和 $2$ 、 $3$ 和 $4$ 是对称的，放案数相同，把它们放在一起 dp ，注意合并 $1, 2$ 后 $4$ 计算完后要乘二，因为可以交换，另外，写的时候当然不是考虑哪个儿子做 $y’, y’’$ 而是枚举到每个儿子时，讨论它已经选好了 $y’, y’’$ 和选当前儿子做 $y’, y’’$ 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include <bits/stdc++.h>
using LL = long long;
const int N = 2e5 + 100, P = 998244353;
struct Edge{ int ne, ver; } e[N << 1];
int h[N], idx = 0, n;
void add(int x, int y){ e[idx] = {h[x], y}, h[x] = idx++; }
void adj(int &x){ x += (x >> 31) & P; }
std::array<int, 3> dp(int x, int fa) //return ([0/1], [2/3], 4)
{
    std::array<int, 3> d, f; //f:d[4]的辅助,d[2/3]的积,d[4]的积
    d = {0, 0, 0}, f = {0, 1, 1};
    for (int i = h[x], y; ~i; i = e[i].ne) if ((y = e[i].ver) != fa)
    {
        auto dy = dp(y, x);
        d[0] = LL(d[0]) * dy[2] % P;
        adj(d[0] += LL(f[2]) * dy[0] % P - P);
        d[1] = LL(d[1]) * dy[1] % P;
        adj(d[1] += LL(f[1]) * dy[0] % P - P);
        d[2] = LL(d[2]) * dy[2] % P;
        adj(d[2] += LL(f[0]) * dy[0] % P - P);
        f[0] = LL(f[0]) * dy[2] % P;
        adj(f[0] += LL(f[2]) * dy[0] % P - P);
        f[1] = LL(f[1]) * dy[1] % P;
        f[2] = LL(f[2]) * dy[2] % P;
    }
    adj(d[0] += f[1] - P), adj(d[2] += d[2] - P);
    return d;
}
int main()
{
    scanf("%d", &n);
    std::memset(h + 1, -1, n << 2);
    for (int i = 1, u, v; i < n; ++i)
    {
        scanf("%d %d", &u, &v);
        add(u, v), add(v, u);
    }
    auto ans = dp(1, -1);
    printf("%d\n", (LL(ans[1]) * 2 + ans[2]) % P);
    return 0;
}

E

考场上鬼的退火，没搞成，正解似乎是网络流，个人感觉是最难的，因为那个建图好难想 网络流弱鸡一只

首先对于每一对 $x, y$ ，把 $a_x, a_y$ 加至大于等于 $\min(b_x, b_y)$ 显然这是对的，然后，建图如下：

  1. 建立源点、汇点 $S, T$
  2. 建立 $n$ 个点代表 $x$ 自己
  3. 建立 $n * 100$ 个点 $(y, i)$ 代表 $a_y$ 要 $\ge i$
  4. 对于所有 $x$ ，连边 $S \to x$ ，权值为 $b_x - a_x$ ，代表 $x$ 要自己打败自己的怪兽
  5. 对于所有询问的 $(x, y)$ ，连边 $x \to (y, b_x -a_y)$ ，权值为 $\infty$ ，代表由 $y$ 打败 $x$ 的怪兽
  6. 对于所有 $(y, i)$ 连边 $(y, i) \to (y, i - 1)$ ，权为 $\infty$ ，代表满足 $(y, i)$ 就满足 $(y, i - 1)$
  7. 对于所有 $(y, i)$ 连边 $(y, i) \to T$ 权值为 $1$

当然，上面所有建立的边、点都是在该怪兽还没被打表的前提下，所以不会有负权边

考虑时间，记 $A$ 为 $a, b$ 的最大值，最大流量是 $O(nA)$ ，而边数是 $O(n^2 + nA)$ ，所以复杂度是 $O(n^3A + n^2A^2)$ 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
#include <bits/stdc++.h>
const int N = 100 + 50, A = 100 + 50, INF = 0x3f3f3f3f;
int n, m, ans = 0, a[N], b[N];
bool mp[N][N];
int S, T, h[N + A * N], idx = 0, q[N + A * N], hh, tt, dep[N + A * N], cur[N + A * N];
struct Edge{ int ne, ver, w; } e[(N * N + N * A) << 1];
void add(int x, int y, int z){ e[idx] = {h[x], y, z}, h[x] = idx++; }
void dad(int x, int y, int z){ add(x, y, z), add(y, x, 0); }
int id(int x, int i){ return n + 100 * (x - 1) + i; }
bool bfs()
{
    hh = tt = 1;
    std::memset(dep, 0, (T + 1) * sizeof(int));
    q[dep[S] = 1] = S, cur[S] = h[S];
    while (hh <= tt)
    {
        int x = q[hh++];
        for (int i = h[x], y; ~i; i = e[i].ne) if (!dep[y = e[i].ver] && e[i].w)
        {
            dep[y] = dep[x] + 1, cur[y] = h[y];
            if (y == T) return true;
            q[++tt] = y;
        }
    }
    return false;
}
int find(int x, int lim)
{
    if (x == T) return lim;
    int res = 0;
    for (int i = cur[x], y, t; ~i && res < lim; i = e[i].ne)
    {
        cur[x] = i;
        if (dep[y = e[i].ver] == dep[x] + 1 && e[i].w)
        {
            t = find(y, std::min(e[i].w, lim - res));
            if (!t) dep[y] = 0;
            else e[i].w -= t, e[i ^ 1].w += t, res += t;
        }
    }
    return res;
}
int dinic()
{
    int flow, res = 0;
    while (bfs())
        while (flow = find(S, INF)) res += flow;
    return res;
}
int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; ++i) scanf("%d %d", &a[i], &b[i]);
    scanf("%d", &m);
    for (int i = 1, x, y, z; i <= m; ++i)
    {
        scanf("%d %d", &x, &y);
        z = std::min(b[x], b[y]);
        if (a[x] < z) ans += z - a[x], a[x] = z;
        if (a[y] < z) ans += z - a[y], a[y] = z;
        mp[x][y] = mp[y][x] = true;
    }
    S = id(n + 1, 1), T = S + 1;
    std::memset(h, -1, (T + 1) * sizeof(int));
    for (int i = 1; i <= n; ++i) if (b[i] > a[i]) dad(S, i, b[i] - a[i]);
    for (int i = 1; i <= n; ++i)
        for (int j = 1; j <= n; ++j) if (mp[i][j] && b[i] > a[j]) dad(i, id(j, b[i] - a[j]), INF);
    for (int i = 1; i <= n; ++i)
        for (int j = 2; j <= 100; ++j) dad(id(i, j), id(i, j - 1), INF);
    for (int i = 1; i <= n; ++i)
        for (int j = 1; j <= 100; ++j) dad(id(i, j), T, 1);
    printf("%d\n", ans + dinic());
    return 0;
}

F

$O(n^3)$ 的暴力 dp 比较显然，设 $d[i, j, k]$ 表示“前 $i$ 次操作， $X$ 有 $j$ 的魔法值， $Y$ 有 $k$ 的魔法值的最大伤害”，直接 dp 即可

正解的话，发现设 $X$ 进行了 $C_X$ 次攻击，分别是第 $x_1, x_2, …, x_{C_X}$ 次那么其贡献为 $\sum x_i - \frac{(C_X + 1)C_X}{2}$ ，所以，最后答案是 $\sum x_i + \sum y_i - \frac{(C_X + 1)C_X}{2} - \frac{(C_Y + 1)C_Y}{2}$ ，现在，我们把操作分成 $5$ 类，考虑它们的影响， 对于本个 $i$ ：

  1. $X, Y$ 的选则已经固定，我们无法改变，直接计算即可
  2. $X, Y$ 的选则都不固定，且相反： $\sum x_i + \sum y_i$ 一定会 $+i$ ，问题是 $C_X, C_Y$ 谁 $+1$
  3. $X, Y$ 的选则都不固定，且相同：要么 $\sum x_i + \sum y_i += 2i$ 且 $C_X, C_Y += 1$ ，要么没有影响
  4. $X$ 的选则固定了：要么 $\sum x_i + \sum y_i += i$ 且 $C_Y += 1$ ，要么没有影响
  5. $Y$ 的选则固定了：要么 $\sum x_i + \sum y_i += i$ 且 $C_X += 1$ ，要么没有影响

直接选显然 sb ，发现当 $1, 2, 3$ 都确定了的时候， $4/5$ 其实可以贪心选，且决策只与 $C_Y/C_X$ 有关，不妨预处理；然后对于 $2$ 枚举有多少个 $C_X + 1$ ，再对于 $3$ 枚举有多少个有影响，最后统计一下答案，总时间 $O(n^2)$ ；需要注意的就是 $1, 4,5$ 中固定的贡献是没有选则必须计算的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#include <bits/stdc++.h>
#define pb push_back
const int N = 8000 + 100;
int n, as, cx1, cy1, ans, cx, cy;
std::vector<int> typ[6];
int dt3[N], dt4[N], dt5[N];
int get(int c){ return (c * (c + 1)) >> 1; }
int calc(std::vector<int> &tp, int c)
{
    int res = 0, t = get(c + 1) - get(c);
    for (int p : tp)
        if (p > t)
        {
            res += p - t;
            ++c, t = get(c + 1) - get(c);
        }
        else break;
    return res;
}
int main()
{
    scanf("%d", &n), as = cx1 = cy1 = 0;
    for (int i = 1, a, b, c, d; i <= n; ++i)
    {
        scanf("%d %d %d %d", &a, &b, &c, &d);
        if (a == c)
        {
            if (a == 2) as += i, ++cx1;
            if (b != d) typ[4].pb(i);
            else if (b == 2) as += i, ++cy1;
        }
        else
        {
            if (b == d)
            {
                typ[5].pb(i);
                if (b == 2) as += i, ++cy1;
            }
            else if (a == b) typ[3].pb(i);
            else typ[2].pb(i), as += i;
        }
    }
    for (int i = 2; i <= 5; ++i) if (typ[i].size()) std::reverse(typ[i].begin(), typ[i].end());
    for (int i = 0; i <= n; ++i) dt4[i] = calc(typ[4], i);
    for (int i = 0; i <= n; ++i) dt5[i] = calc(typ[5], i);
    for (int i = 0; i < typ[3].size(); ++i) dt3[i + 1] = dt3[i] + (typ[3][i] << 1);
    for (int i = typ[2].size(), t; ~i; --i)
        for (int j = typ[3].size(); ~j; --j)
        {
            cx = cx1 + i + j, cy = cy1 + typ[2].size() - i + j, t = as + dt3[j];
            t -= get(cx) + get(cy);
            t += dt4[cy] + dt5[cx];
            ans = std::max(ans, t);
        }
    printf("%d\n", ans);
    return 0;
}