然而我 dp 废的一比
优化dp4
才发现这个还没写……
上一篇:优化dp3
wqs 二分
(并不保证真确性的)定义
以下全是自己的理解:感觉就是用来求一个“选 $m$ 个,最优化”的问题,更具体的,设选 $x$ 个的最大权值为 $f(x)$ ,wqs 二分要求 $f(x)-x$ 图像是这样(就是先随着可选个数增多变优,后来因为必须要选 $x$ 个导致变坏),形式化的,其实是要求它是个凸函数: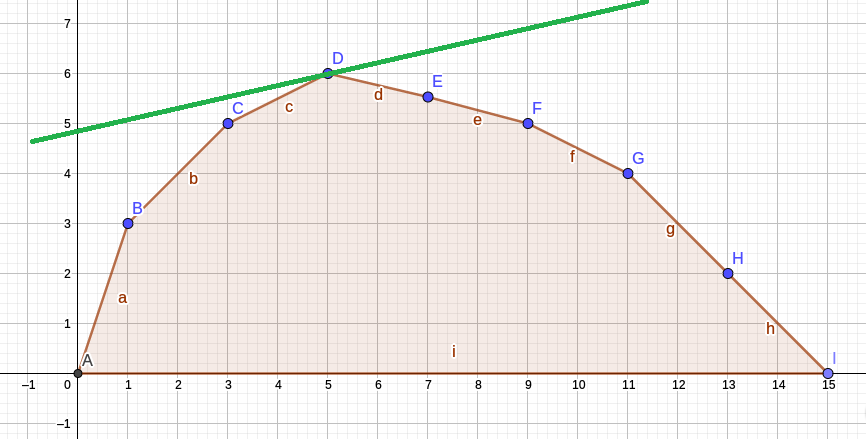
如图,设绿色直线为 $y = kx + b$ ,由切点 $D(x_D, f(x_D))$ 得 $b = f(x_D) - kx_D$ ,考虑到这是切线,显然对于一个确定的 $k$ , $x_D$ 是使 $b$ 最大的点,那么可以二分一个 $k$ ,把每个物品的价值 $-k$ (如果是代价就 $+k$ ),然后做没有个数限制的 dp 求出最大的价值和就是 $b$ ,此时对应的 $x$ (如绿线对应的 $x_D$ )若比 $m$ 大,说明 $k$ 应继续变大;若比 $m$ 小,$k$ 应该变小;若相等,则用 $k, x/m$ 计算得到 $f(m)$
值得一提的是,很多时候如果 $x, f(x)$ 都是整数,那么 $k$ 也可以只在整数范围二分:考虑求导,有 $f’(x) = k$ ,大部分情况下 $f(x)$ 的导函数 $f’(x)$ 都是“比较好看的”,加上 $x$ 是整数,那么 $k$ 一半也是整数
但是,整数又会遇到一个问题:如果一条切线过了几个点(包括 $m$ )怎么办(更具体的,当斜率为 $k$ 时 $x = m - 1$ ,斜率变化 $1$ 时 $x = m + 1$ )?其实此时我们不也是算出了 $m$ 的斜率吗,直接就用此时的 $k$ 就好了(优先用小的那个算,即 $x = m - 1$ 那个)
带权二分的好处在于,对于要求“选则恰好 $k$ 个“,我们 dp 时几乎不可避免的要给 $k$ 一维,这让状态数(和时间复杂度)直接乘了个 $n$ (个数),而 wqs 二分可以避免加一维,把 $n$ 优化至 $\log v$ (权值)
另外,一个细节是,向下取整( l + r >> 1 )和向 $0$ 取整( $(l + r) / 2$ )是不一样的;且 $l, r$ 的初始值是斜率最大值和最小值啊,如果 $f(x)$ 是上凸的,然后 $x$ 的范围是 $[0,n]$ ,那么 $r$ 应该等于 $f(1)−f(0)$ 的最大可能值,$l$ 同理等于 $f(n)−f(n−1)$ 的最小可能值
例题十二
经典题:Tree I
思路
二分一个 $k$ ,对于每条白边,把权值改为 $c - k$ ,直接做最小生成树即可,时间 $O(m \log m \log k \alpha(n))$ ( $k$ 是边权),可以黑白边分开排序,每次合并,时间 $O(m \alpha(n) \log k + m \log m)$
细节是一条切线过几个点的情况,此时明显白边权值与黑边权值相等,我们优先选白边,还有 $k$ 可以为负数
(所以这和 dp 有啥关系啊)
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
| #include <bits/stdc++.h>
#define fi first
#define se second
using PII = std::pair<int, int>;
const int N = 5e4+ 100, M = 1e5 + 100;
int n, m, num, ans, cta = 0, ctb = 0;
struct Edge{ int u, v, w, c; } e[M], a[M], b[M];
int fa[N], rk[N];
int get(int x){ return fa[x] == x ? x : fa[x] = get(fa[x]); }
void merge(int x, int y)
{
if (rk[x] > rk[y]) std::swap(x, y);
fa[x] = y, rk[y] += rk[x] == rk[y];
}
PII chk(int k)
{
int i = 1, j = 1, ct = 0, x, y;
PII res = {0, 0};
while (i <= cta && j <= ctb)
{
if (a[i].w - k < b[j].w) e[++ct] = a[i++], e[ct].w -= k;
else e[++ct] = b[j++];
}
while (i <= cta) e[++ct] = a[i++], e[ct].w -= k;
while (j <= ctb) e[++ct] = b[j++];
for (i = 1; i <= n; ++i) fa[i] = i, rk[i] = 1;
for (i = 1; i <= ct; ++i)
{
x = get(e[i].u), y = get(e[i].v);
if (x == y) continue;
res.fi += e[i].w;
res.se += e[i].c == 0;
merge(x, y);
}
return res;
}
int main()
{
scanf("%d %d %d", &n, &m, &num);
for (int i = 1; i <= m; ++i)
{
scanf("%d %d %d %d", &e[i].u, &e[i].v, &e[i].w, &e[i].c);
++e[i].u, ++e[i].v;
if (e[i].c == 0) a[++cta] = e[i];
else b[++ctb] = e[i];
}
std::sort(a + 1, a + cta + 1, [&](Edge x, Edge y){ return x.w < y.w; });
std::sort(b + 1, b + ctb + 1, [&](Edge x, Edge y){ return x.w < y.w; });
int l = -101, r = 101, mid;
PII t;
while (l <= r)
{
mid = (l + r) >> 1;
t = chk(mid);
if (t.se <= num)
{
ans = t.fi + mid * num;
l = mid + 1;
}
else r = mid - 1;
}
printf("%d\n", ans);
return 0;
}
|
例题十三
看看真正的 dp 题(不难发现大部分时候 dp 都是套在 wqs 二分内部的):林克卡特树
思路
为了方便记题目中的 $k$ 为 $num$ 显然切断 $num$ 条边后原树变成 $num + 1$ 个联通块(更进一步,它们都是树),我们求出每棵树的直径(最长链,可以是点),用 $num$ 条权为 $0$ 的边连起来就是最优解
考虑树形 dp ,套路的设 $d[i, j]$ 表示”点 $i$ 的子树中有 $j$ 条链的最大值”,然后发现没法转移,没法转移的关键问题是,当考虑合并 $u, v$ 两个点代表的联通块集合时,会出现两个链合并成一条链/链数不变/链数加 $1$ 三个情况,我们当前信息无法指导我们如何转移
考虑加一维,不难发现在最后选的链中每个点的度数只有 $0/1/2$ ,于是令 $d[i, j, k](k = 0/1/2)$ 表示”点 $i$ 的子树中有 $j$ 条链,且 $i$ 的度数为 $k$ 的最大值“,那么转移就分讨设 $v$ 为 $u$ 的儿子:
- 不选 $(u, v)$ : $d[u, j_1, k_1] + d[v, j_2, k_2] \to d[u, j_1 + j_2, k_1]$
- 选则 $(u, v)$ : $d[u, j_1, k_1] + d[v, j_2, k_2] \to d[u, j_1 + j_2 + dt, k_1 + 1]$ ,其中 $k_1, k_2 \ne 2$ , $dt = [k_1 == 0 \wedge k_2 == 0] - [k_1 == 1 \wedge k_2 == 1]$
那么边界显然就是 $d[i, 0, 0] = 0$ 其它都是 $-\infty$ ,吗?发现如果是以一个点作为链,那就是 $d[i, 1, ?] = 0$ ,但 $?$ (也就是这个点的度)该是多少呢?显然我们不能让这个点与其它任何点相连,所以是 $2$ ,即 $d[i, 1, 2] = d[i, 0, 0] = 0$ 其它都是 $-\infty$ ,于是 dp ,答案就是 $\max(d[root, num, 0/1/2])$ ,直接 dp 时间为 $O(n * num * 3)$ ,我们发现很难优化,因为转移已经是 $O(1)$ 了,时间瓶颈在状态数,现在我们要么减少计算的状态数(即只计算一部分状态),要么减少状态数(即修改状态的定义)
此时不难发现 这篇 blog 讲的是 wqs 二分 此题也是”选 $num$ 个“的形式,我们把 $num = 0 \sim 100$ 的答案依次求一下,发现这是一个凸函数(不会证,具体做题时靠感觉 + 打表 + 猜想),上 wqs 二分,把第二维直接去掉,转移时发现边数减少就加一个 $k$ ,否则减一个 $k$ (这个 $k$ 是二分的)
最后是 wqs 二分的经典问题:凸包上多点共线怎么解决;我们打个结构体 dp 时优先转移边数少的即可,注意去掉第二维后出现自己转移到自己的情况,用临时数组避免多次转移
代码
$l, r$ 初始值一定要够大,注意是 $num + 1$ 个联通块
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
| #include <bits/stdc++.h>
using LL = long long;
const int N = 3e5 + 100, inf = 0x3f3f3f3f;
const LL INF = 1e18;
int n, num, l, r, mid, h[N], idx = 0;
struct Edge{ int ne, ver, w; } e[N << 1];
struct DP
{
LL v; int num;
bool operator < (DP x) const { return v == x.v ? num > x.num : v < x.v; }
DP operator + (DP x){ return {v + x.v, num + x.num}; }
} d[N][3], as, td[3];
LL ans;
void add(int x, int y, int z){ e[idx] = {h[x], y, z}, h[x] = idx++; }
template<typename T>
bool cmx(T &x, T y){ return x < y ? x = y, true : false; }
void dp(int x, int fa)
{
for (int i = h[x], y; ~i; i = e[i].ne) if ((y = e[i].ver) != fa)
{
dp(y, x);
for (int j = 0; j <= 2; ++j) td[j] = {-INF, inf};
for (int j = 0; j <= 2; ++j)
for (int k = 0; k <= 2; ++k) cmx(td[j], d[x][j] + d[y][k]);
cmx(td[1], d[x][0] + d[y][0] + DP{e[i].w - mid, 1});
cmx(td[1], d[x][0] + d[y][1] + DP{e[i].w, 0});
cmx(td[2], d[x][1] + d[y][0] + DP{e[i].w, 0});
cmx(td[2], d[x][1] + d[y][1] + DP{e[i].w + mid, -1});
for (int j = 0; j <= 2; ++j) d[x][j] = td[j];
}
}
int main()
{
scanf("%d %d", &n, &num);
memset(h + 1, -1, n << 2);
for (int i = 1, u, v, w; i < n; ++i)
{
scanf("%d %d %d", &u, &v, &w);
add(u, v, w), add(v, u, w);
}
l = -1e12, r = 1e12;
while (l <= r)
{
mid = (l + r) >> 1;
for (int i = 1; i <= n; ++i)
{
d[i][0] = {0, 0};
d[i][1] = {-INF, inf};
d[i][2] = {-mid, 1};
}
dp(1, 0);
as = d[1][0], cmx(as, d[1][1]), cmx(as, d[1][2]);
if (as.num <= num + 1)
{
ans = as.v + LL(mid) * (num + 1);
r = mid - 1;
}
else l = mid + 1;
}
printf("%lld\n", ans);
return 0;
}
|
未完待续?
