神仙数学题,感觉很考思维
题意
$n$ 堆石子,每堆有 $v_i$ 个,两个人 $A, B$ ,每次分别可以取 $a, b$ 个,且满足 $a, b \in [1, m]$ ,给定 $n, m, v$ 求满足以下条件的 $(a, b)$ 的对数:
- $A$ 必胜
- $B$ 必胜
- 先手必胜
- 后手必胜
思路
瞟题解瞟了一下午才看懂
先考虑已知 $(a, b)$ 如何判胜负,不妨让 $a \le b$ ,显然 $v_i$ 和 $v_i \mod (a+ b)$ 等价(赢家一定可以通过 $k$ 此次和对方一起取,在胜负不变的情况下使石子多 $k(a + b)$ 个),我们讨论模后的 $v_i$ :
- $v_i \in [0, a)$ ,它没用
- $v_i \in [a, b)$ ,它只有 $a$ 可以取,所以只要存在这种情况, $A$ 必胜( $A$ 可以先留着这堆和 $B$ 一起取其它堆石子),它是有利于小者的
- $v_i \in [b, 2a)$ ,它对 $A, B$ 都只可取一次,是中性的,注意 $b \ge 2a$ 时不存在这种情况
- $v_i \in [\max(2a, b), a + b)$ ,若 $A$ 先手取它,它变成 $2$ ,使 $A$ 必胜;若 $B$ 先手取它,它变成 $1$ ,没用
于是:
- 当存在 $2$ 或者存在两个以上 $4$ 时,小者必胜
- 否则,若只存在一个 $4$ ,若有小者 + 先手则必胜;否则统计 $3$ 的个数,奇数个小的(同时是后手)胜,偶数个大的胜
- 否则,统计 $3$ 的个数,奇数个先手胜,偶数个后手胜
于是枚举 $(a, b)$ 就有了 $O(m^2n)$ 的做法,考虑优化
枚举 $sum = a + b$ ,我们钦定 $B$ 为后手(但不保证 $a, b$ 的大小关系)来计算后手胜的个数,在 $b$ 从小增大的途中,必定存在 $pos$ 使 $b$ 大于 $pos$ 后必败(显然后手、大的是不利的),更具体的,如图:
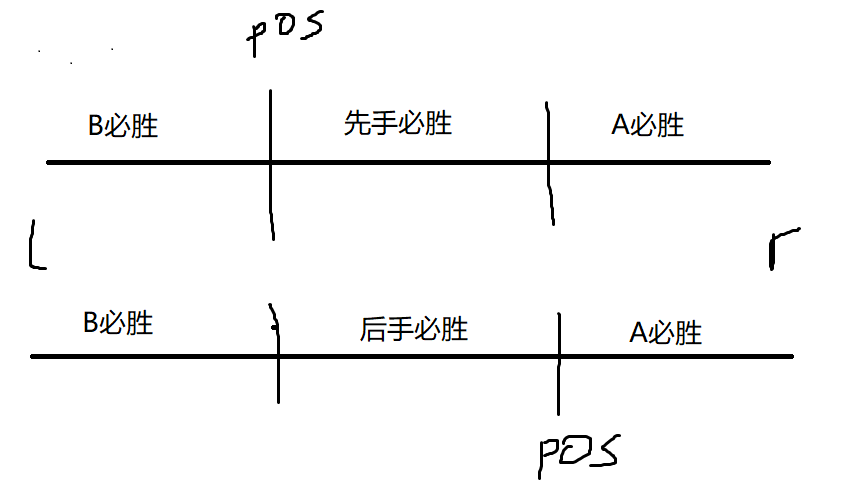
$A, B$ 必胜显然是对称的,一样多,就是 $\min(pos - l + 1, r - pos)$ 个,那么后手必胜就有 $pos - l + 1 - \min(pos - l + 1, r - pos)$ 个,先手必胜最后用总方案数减即得
那么现在考虑如何如何求 $pos$ ,大力分讨,同样设 $v_i$ 为模后的:
若 $b < a$ ,则它的胜利条件为以下两者之一:
- 存在 $v_i \in [b, a)$
- 存在多于两个 $v_i \in [2b, sum)$
对于第二个,考虑记录最大值 $mx$ 和次大值 $mx2$ ,那么 $b \le \frac{mx2}{2}$ 都满足第二个,所以 $pos \ge \frac{mx2}{2}$
对于第一个,即 $b \le v_i < sum - b$ ,得 $b \le v_i$ 和 $b < sum - v_i$ 即 $b \le sum - v_i - 1$ ,所以 $b \le \min(v_i, sum - v_i - 1)$ ,由于存在即可, $pos$ 当取所有 $v_i$ 计算得的最大值
若 $b = a$ ,统计 $v_i \ge \frac{sum}{2}$ 的个数,偶数数个则可以使 $pos = \frac{sum}{2}$ ;这里结束后,若 $pos < \frac{sum}{2}$ ,说明已经无法在让 $pos$ 变大了(过不去 $b = a = \frac{sum}{2}$ 这个点),直接返回
若 $b > a$ ,则它的胜利条件必须满足:
- 所有 $v_i \in [0, a) \cup [b, 2a)$
我们有 $0 \le v_i < sum - b$ 或 $b \le v_i < 2(sum - b)$ ,化简得 $b \le \max(v_i, sum - v_i - 1)$ , $b \le sum - \frac{v_i}{2} - 1$ ,最后一个条件可以直接带 $mx$ ,第一个只好枚举,由于是必须满足,所以 $pos$ 当取所有计算值的最小值
代码
1 |
|