感觉和 KMP 关系不大啊

Z函数（拓展KMP）

定义

故名思意， Z 函数是个函数，若我们定义一个长度为 $n$ 的字符串以第 $i$ 个字符开头，第 $j$ 个字符结尾（下标从 $1$ 开始）的子串为 $s[i\sim j]$ ，再定义 $LCP(x,y)$ 代表字符串 $x,y$ 的最长公共前缀长度，那么，有 $Z[i]=LCP(s[i\sim n],s[0\sim n])$ ，即 $Z[i]$ 表示以 $i$ 开头的后缀与原串的最长公共前缀

求法

直接求显然不好，类似 kmp 考虑用已有的信息，结论是，我们同时维护已与前缀匹配上的位置为 $s[l,r]$ ，如有多个（肯定有多个）取 $r$ 最大

当枚举到 $i$ 时，把 $Z[i]$ 初始化为 $min(Z[i-l+1],r-i+1)$ （要保证 $i\le r$ ），而每次计算完后用 $Z[i]$ 跟新 $l,r$ ，关于正确性，对图理解很显然：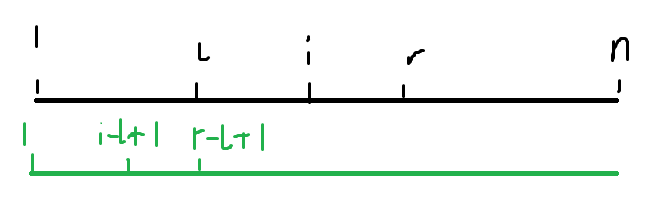

考虑时间复杂度，由于 $l,r$ 单调，直接用初始化匹配的复杂度是线性的，而暴力匹配时，原串的每个字符最多被匹配一次，所以是 $O(n)$ 的

注意， $Z[1]$ 要单独处理

代码

板子

#include <bits/stdc++.h>
#define int LL
using LL = long long;
const int N = 2e7 + 100;
char a[N], b[N];
int la, lb, Z[N], p[N], ans;
void get_Z(char x[], int len)
{
    Z[1] = len;
    for (int i = 2, l = 0, r = 0; i <= len; ++i)
    {
        if (i <= r) Z[i] = std::min(Z[i - l + 1], r - i + 1);
        while (Z[i] + i <= len && x[Z[i] + 1] == x[Z[i] + i]) ++Z[i];
        if (i + Z[i] - 1 > r) r = i + Z[i] - 1, l = i;
    }
}
void exkmp(char x[], int len, char y[]) //y已有Z数组
{
    for (int i = 1, l = 0, r = 0; i <= len; ++i)
    {
        if (i <= r) p[i] = std::min(Z[i - l + 1], r - i + 1);
        while (p[i] + i <= len && y[p[i] + 1] == x[p[i] + i]) ++p[i];
        if (i + p[i] - 1 > r) r = i + p[i] - 1, l = i;
    }
}
signed main()
{
    scanf("%s %s", a + 1, b + 1);
    la = strlen(a + 1), lb = strlen(b + 1);
    get_Z(b, lb), ans = 0;
    for (int i = 1; i <= lb; ++i) ans ^= (Z[i] + 1) * i;
    printf("%lld\n", ans);
    exkmp(a, la, b), ans = 0;
    for (int i = 1; i <= la; ++i) ans ^= (p[i] + 1) * i;
    printf("%lld\n", ans);
    return 0;
}