系统的看一下
前面递归式学习时浅尝其苦,现在真的来受苦
矩阵
前置知识
定义类
矩阵:由 $m \times n$ 个元素排列成 $m$ 行 $n$ 列的数表叫矩阵,即:
$$
\begin{aligned}
A =
\begin{bmatrix}
a_{1, 1}, a_{1, 2}, …, a_{1, n} \\
a_{2, 1}, a_{2, 2}, …, a_{2, n} \\
… \\
a_{m, 1}, a_{m, 2}, …, a_{m, n} \\
\end{bmatrix}
\end{aligned}
$$奇/偶排列:逆序对数为奇/偶数的排列,一下记排列 $a_1, a_2, …, a_n$ 的逆序对数为 $\tau(a_1, a_2, …, a_n)$
方阵: $n \times n$ 的矩阵,一般记作方阵 $A, B, C …$ ,其中 $n$ 叫做该方阵的阶
行列式:一个 $n$ 阶方阵的行列式等于取自所有不同行不同列的 $n$ 个元素的乘积的“代数和”(即按奇/偶排列带负/正号),记作 $det(A)$ (也有记作 $\mid A \mid$ ),形式化的:
$$
\begin{aligned}
对于 n 阵方阵 A & =
\begin{bmatrix}
a_{1, 1}, a_{1, 2}, …, a_{1, n} \\
a_{2, 1}, a_{2, 2}, …, a_{2, n} \\
… \\
a_{n, 1}, a_{n, 2}, …, a_{n, n} \\
\end{bmatrix} \\
其行列式 det(A) & =
\begin{vmatrix}
a_{1, 1}, a_{1, 2}, …, a_{1, n} \\
a_{2, 1}, a_{2, 2}, …, a_{2, n} \\
… \\
a_{n, 1}, a_{n, 2}, …, a_{n, n} \\
\end{vmatrix} \\
& = \sum_{j_1, j_2, …j_n 是 1 \sim n 的一个排列} (-1)^{\tau(j_1, j_2, …, j_n)} a_{1, j_1} a_{2, j_2} … a_{n, j_n}
\end{aligned}
$$
不难看出,直接求 $det$ 是 $O(n!)$ 的代数余子式:把一个 $n$ 阶行列式去掉第 $i$ 行和第 $j$ 列后,留下的 $n - 1$ 阶行列式叫做元素 $a_{i, j}$ 的余子式,记作 $M_{i, j}$ ,记 $A_{i, j} = (-1)^{i + j} M_{i, j}$ ,叫做 $a_{i, j}$ 的代数余子式
主/副对角线:对于一个方阵,所有 $i = j$ 的元素 $a_{i, j}$ 组成其主对角线;所有 $i + j = n + 1$ 的元素 $a_{i, j}$ 组成其副对角线
上/下三角矩阵:主对角线左下方/右上方全为 $0$ 的矩阵
同型矩阵:行列数一样的矩阵
主子式:在 $n$ 阶行列式中,任意选取 $i$ 个行号,再选取与行号相同的列号,只保留所选行、列的行列式即为 $n$ 阶行列式的 $i$ 阶主子式
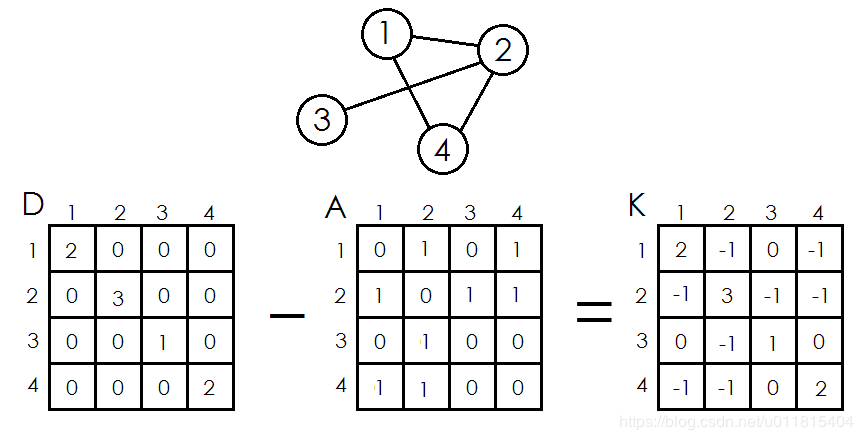
给定一个无向图 $G(V, E)$
度数矩阵 $D$ :当 $i \ne j$ 时, $D[i][j] = 0$ ,否则 $D[i][j] = 点 i(j) 的度数$
邻接矩阵 $A$ :当 $(u, v) \in E$ 时, $A[u][v] = 1$ ,否则 $A[u][v] = 0$
基尔霍夫矩阵( Kirchhoff ) $K$ ,也称拉普拉斯算子:定义为 $K = D - A$ ,如图:
关联矩阵:对于一个 $n$ 个点 $m$ 条边的无向图,我们把边任意定向,那么其关联矩阵是一个 $n$ 行 $m$ 列的矩阵,其中元素满足:
$$
b_{i, j} =
\begin{cases}
-1 & (i 是边 j 的终点) \\
1 & (i 是边 j 的起点) \\
0 & (其它)
\end{cases}
$$
计算类
线性运算:
加法:两个同型矩阵 $A, B$ 的加法运算得到同型矩阵 $C$ ,且 $C$ 中元素满足 $c_{i, j} = a_{i, j} + b_{i, j}$
减法:两个同型矩阵 $A, B$ 的加法运算得到同型矩阵 $C$ ,且 $C$ 中元素满足 $c_{i, j} = a_{i, j} - b_{i, j}$
数乘:一个矩阵 $A$ 乘一个数 $\lambda $ 得到同型矩阵 $C$ ,且 $C$ 中元素满足 $c_{i, j} = \lambda a_{i, j}$
显然,数乘满足分配律和结合律
矩阵乘法:若 $A$ 是 $m \times n$ 的矩阵, $B$ 是 $n \times p$ 的矩阵,它们的乘积是一个 $m \times p$ 的矩阵 $C$ ,且满足 $c_{i, j} = \sum_{r = 1}^n a_{i, r} b_{r, j}$
矩阵乘法满足结合律、左/右分配律,但没有交换律
转置:把矩阵的行换成同序数的列叫做矩阵的转置,记作 $A^{T}$ ,例如:
$$
\begin{bmatrix}
1, 2 , 3 \\
4, 5, 6 \\
\end{bmatrix}
^{T}
=
\begin{bmatrix}
1, 4 \\
2, 3 \\
5, 6 \\
\end{bmatrix}
$$
明显有以下运算律:
$$
\begin{aligned}
& (A^T)^T = A \\
& (\lambda A)^T = \lambda A^T \\
& (AB)^T = B^T A^T (这里注意顺序)\\
\end{aligned}
$$行列式的数学计算式: $n$ 阶方阵的行列式等于其任意行/列元素与对应代数余子式乘积之和,即 $det(A) = \sum_{j = 1}^n a_{i, j} A_{i, j} = \sum_{i = 1}^n a_{i, j} A_{i, j}$ (注意代数余子式是有符号的)
矩阵快速幂
一般的,对于线性递推式 $f_i = a_1 f_{i - 1} + a_2 f_{i - 2} + … + a_k f_{i - k}$ ,我们令 $F = \begin{bmatrix} f_{i - 1} \\ f_{i - 2} \\ … \\ f_{i - k} \end{bmatrix}, F’ = \begin{bmatrix} f_{i} \\ f_{i - 1} \\ … \\ f_{i - k + 1} \end{bmatrix}$ ,不难得到转移矩阵 $A = \begin{bmatrix} a_1 & a_2 & … & a_{k - 1} &a_k \\ 1 &0 &… &0 &0 \\ 0 &1 &… &0 &0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 &0 &… &1 &0 \end{bmatrix}$ ,于是有 $F’ = AF$ ,那么,若 $F_0$ 已知,则 $F_i = A^i F_0$ ,可以先用类似快速幂的方法求 $A^i$ ,把时间降至 $O(k^3 \log n)$
行列式
性质
关于行列式,有几个性质:
交换对应方阵的 $1$ 行和 $1$ 列(进行一次矩阵转置),行列式不变;直接定义展开可证,其实没啥用
交换对应方阵的 $2$ 行(列),行列式取反;
简证:交换一个排列中的两个数,除开它们两个,其它数的逆序对数一定成对变化(变化偶数),只有它们两个导致逆序对变 $1$ ,所以 $det$ 中每一项都取反
若有一行(列)相等,行列式为 $0$
简证:交换相等的这两行,得 $det = -det$
任意行(列)所有元素等比例变化,则行列式也等比例变化;展开后由乘法分配律可得
任意两行/列成比例,行列式为 $0$ ;由性质 $3, 4$ 可得
如果行列式对应方阵 $A$ 中有一行(列),是对应2个方阵 $B, C$ 中分别的 $2$ 行(列)所有元素之和,且 $A$ 中其它元素都等于 $B, C$ 中对应元素,则有 $det(A) = det(B) + det(C)$ ;写成行列式,由乘法分配律可证
把一个矩阵的一行(列)的值全部乘一个常数加到另一行(列)上,行列式值不变;由性质 $5, 6$ 可得
上三角矩阵的行列式就等于对角线元素乘积;展开可得
$det(AB) = det(A) \times det(B)$
计算
直接计算行列式是 $O(n!)$ ,用数学算法要大量分治递归(实测 $n > 12$ 时几乎就是暴力),所以我们考虑性质 $8$ ,只要通过行列式的变换把它变成上三角矩阵,我们就可以 $O(n)$ 计算了,又由性质 $2, 4, 7$ ,我们可以直接高斯消元 $O(n^3)$
实现时注意若没有逆元,要辗转相除,此时虽然多个 $\log $ ,但每次做两次消元 $a_{i, i}$ 至少会变为原来的一半,而这个势能是不会上升的,均摊下去复杂度为 $O(n^2 (\log p + n))$
1 |
|
当然,若模数是质数,还是直接取逆元好,而且长得和gauss 消元更像(但其实这是高斯-约旦消去法):
1 |
|
关于行列式的运用,还有几个东西,我懒了,可以查阅 OI Wiki ,它们是
LGV 引理
BEST 定理
Binet-Cauchy定理
咕咕咕
Matrix-Tree 定理(矩阵树定理)
无向图 $G$ 的所有生成树个数等于其 kirchhoff 矩阵 $K(G)$ 任何一个 $n - 1$ 阶主子式的绝对值
几条引理
由于证明太麻烦就不写了,可以参考这个
一个 kirchhoff 矩阵 $K$ 的行列式总是为 $0$
如果图 $G$ 不构成树,那么 $K(G)$ 的任意一个 $n - 1$ 阶主子式都为 $0$
如果图 $G$ 构成树,则 $K(G)$ 的任意一个 $n - 1$ 阶主子式绝对值都为 $1$
设图 $G$ 的关联矩阵为 $B$ ,有 $B B^T = K$
常见变形
- 若存在必选边,考虑将必选边连接的点缩点,对压缩后的图求生成树
- 如果图中边有边权,可以把度数矩阵 $D$ 变成边的权值和,直接用Matrix-Tree 定理,求得的就是所有生成树边权乘积的总和
- 如果求有向图生成树,首先要把邻接矩阵 $A$ 变成有向图的邻接矩阵,然后对于 $D$ ,如果它记录的是到该点入的边权总和,那么求得的就是外向树 (从根向外),即 $D[i][j] = \sum_{j = 1}^n A[j][i]$ ;类似的,如果它记录的是到该点出的边权总和,那么求得的就是内向树 (从外向根),关于如何保证根,巨佬们说:去掉第 $k$ 行 $k$ 列就是以 $k$ 为根
线性方程
一般来说,线性方程形式如下:
$$
\begin{cases}
a_{1, 1} x_1 + a_{1, 2} x_2 + … + a_{1, n} x_n = b_1 \\
a_{2, 1} x_1 + a_{2, 2} x_2 + … + a_{2, n} x_n = b_2 \\
… \\
a_{m, 1} x_1 + a_{m, 2} x_2 + … + a_{m, n} x_n = b_m \\
\end{cases}
$$
我们常记为 $AX = B$ ,其中 $A, B$ 是系数/常数矩阵,而 $X$ 是未知数构成的矩阵( $X, B$ 也可理解为向量)
guass 消元
不多说,给代码
实数版:
1 |
|
取模版:
1 | int qpow(int x, int y) |
LU分解法
在系数矩阵不变,仅仅是常数改变时,LU分解法有很大的优势
顾名思义,LU分解就是把系数矩阵 $A$ 分解成两个矩阵 $L, U$ ,满足 $LU = A$ 且 $L$ 为下三角矩阵且主对角线为 $1$ , $U$ 为上三角矩阵,即:
$$
\begin{bmatrix}
a_{1, 1} & a_{1, 2} & … & a_{n, n} \\
a_{2, 1} & a_{2, 2} & … & a_{2, n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{n, 1} & a_{n, 2} & … & a_{n, n} \\
\end{bmatrix}
=
\begin{bmatrix}
1 & 0 & … & 0 \\
l_{2, 1} & 1 & … & 0 \\
\vdots & \vdots & \ddots & \vdots \\
l_{n, 1} & l_{n, 2} & … & 1 \\
\end{bmatrix}
\begin{bmatrix}
u_{1, 1} & u_{1, 2} & … & u_{1, n} \\
0 & u_{2, 2} & … & u_{2, n} \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & … & u_{n, n} \\
\end{bmatrix}
$$
于是,有 $LUX = B$ ,即 $UX = Y, LY = B$
你可能在担心该如何求 $L, U, X, Y$ ,没有关系,前人已经帮我们总结了公式(这也叫 Doolittle 算法):
求 $L, U$ ,对于 $k = 1, 2, …, n$ :
$$
\begin{cases}
u_{k, j} = a_{k, j} - \sum_{r = 1}^{k - 1} l_{k, r} u_{r, j} & j = k, k + 1, …, n \\
u_{i, k} = (a_{i, k} - \sum_{r = 1}^{k - 1} l_{i, r} u_{r, k}) / u_{k, k} & i = k, k + 1, …, n\\
l_{k, k} = 1
\end{cases}
$$求 $Y$ ,对于 $k = 1, 2, …, n$ :
$$
y_k = b_k - \sum_{r = 1}^{k - 1} l_{k, r} y_{r}
$$求 $X$ ,对于 $k = n, n - 1, …, 1$ :
$$
x_k = (y_k - \sum_{r = k + 1}^n u_{k, r} x_r) / u_{k, k}
$$
不难发现,第一步是 $O(n^3)$ ,另外两步都是 $O(n^2)$ 的,要支持取模也很方便(背公式就好了,这不比高斯香?)
ps:如果方程有多解或者无解, $L, U$ 中会有 nan ,注意处理
矩阵求逆
在 guass 的同时对单位矩阵进行一样的操作即可(一定要先操作单位矩阵)
ps:其实,对于 $AX = B$ ,可以 $X = A^{-1} B$ 来解
1 |
|