日本オリジナル輸入問題
题意
给定 $L, R \le 2^{60}$ ,求在区间 $[L, R]$ 中选若干个或起来有多少种取值
思路
首先 打个表 通过充分的思考,我们可以发现其实选超过 $2$ 个数和选 $2$ 个数答案是一样的,简证 口胡 如下:
对于一种选法,假设我们选了数 $a_1, a_2, …, a_n$ ,且 $a_1 or a_2 or … or a_n = A$ ,我们找到二进制下最高的一个不全相同的位置,如图:
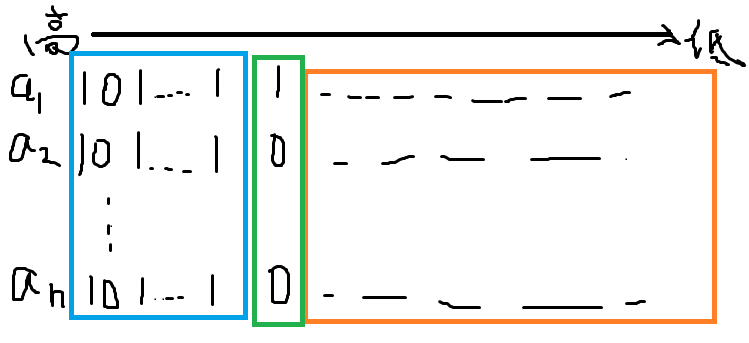
前面的高位(蓝色)每个 $a_i$ 都相同,后面的低位(橘色)我们不管,绿色框住的就是最高不同位
我们任取一个 $a_i$ 该位为 $1$ (如图中 $a_1$ ),再取一个 $a_j$ 该位为 $0$ (如图中 $a_2$ ),然后,我们把 $a_i$ 后面的低位(橘色)全赋为 $0$ ,记为 $a_i’$,赋完后 $a_i’$ 该位仍然为 $1$ ,则有 $a_j < a_i’ \le a_i$ ,由于 $a_i, a_j \in [L, R]$ ,故 $a_i’ \in [L, R]$ ;类似的,我们把 $a_j$ 后面的低位(橘色)赋值为和 $A$ 相同(仅橘色部分相同),有 $a_j \le a_j’ < a_i$ ,即 $a_j’ \in [L, R]$ ;最后,我们用 $a_i’ or a_j’ = A$ 来替代这 $n$ 个数
综上, 选超过 $2$ 个数和选 $2$ 个数答案是一样
然后考虑从 $[L, R]$ 中选一个或两个数有多少种取值,我们找到 $L, R$ 的二进制下最高的不同位,记为 $bit$ (很明显 $R$ 该位为 $1$ ),再取 $t$ 是前 $bit$ 位都和 $R$ 相同,后面全为 $0$ ,如图
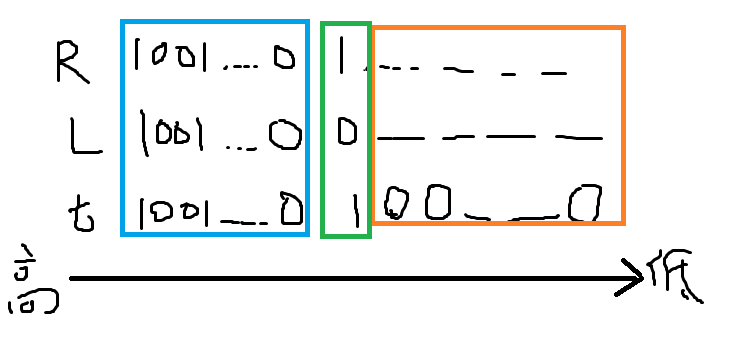
绿色是第 $bit$ 位,蓝色部分都相同, $L, R$ 的橙色部分不确定,但 $t$ 的橙色部分全为 $0$ ,显然 $L < t \le R$ ,我们把区间 $[L, R]$ 分成 $[L, t)$ , $[t, R]$ 两段分类讨论,最后取并集即可,不妨设我们选的数为 $x, y$ 且 $x < y$ (若只选了一个,就设选的为 $x$ ):
1) $x, y \in [L, t)$
此时 $x or y$ 一定属于 $[L, t)$ (或运算不会变小,且或后第 $bit$ 一定为 $0$ ),而且,注意到可以只选一个,所以一定可以取遍 $[L, t)$
2) $x, y \in [t, R]$
你会发现这个问题就是原问题,只不过 $L$ 变成了 $t$ ,但 $t$ 比 $L$ 多一个关键性质: $t$ 的 $bit$ 位以后都是 $0$ ,这意味着,若 $R$ 在 $bit$ 位以后最高的 $1$ 在第 $k$ 位,那么 $x or y$ 或者 $x$ 在 $bit$ 位以后最高的 $1$ 在最高也只能在第 $k$ 位,而 $k$ 位以后都可以为 $1$ ,因为区间 $[t, R]$ 是连续的,而 $t$ 的第 $k$ 位即以后都是 $0$ ,每次加 $1$ ,要变到 $R$ ,即第 $k$ 位为 $1$ ,则 $k$ 以下的位置一定是出现过为 $1$ 的情况的,于是,构造 $p$ 如下:
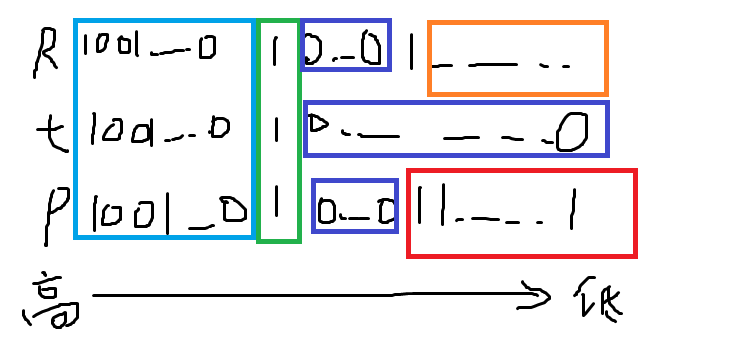
蓝色高位都相同,绿色是第 $bit$ 位,紫色部分都为 $0$ ,红色部分都为 $1$ ,橙色部分任意, $R$ 未被框起来的是第 $k$ 位
于是 $x or y$ 就取值于 $[t, p]$ ( $x$ 取值为 $[t, R]$ 被包含了)
3) $x \in [L, t), y \in [t, R]$
此时一定是取了两个数的情况
下限很好求,就是 $L or t$ ,对于上限,由于前 $bit$ 位最大也只能和 $R$ 一样,而那么最大就是 $bit$ 位以后全为 $1$ ,构造也很简单,就是 $x = t - 1, y = t$ 即可,由于两个区间都是连续的,所以 $x or y \in [L or t, t or (t - 1)]$
代码
不难发现前两个情况可以连起来,记得特判区间长度只有 $1$ 的情况
1 |
|