Dyd's Blog

He who has a strong enough why can bear almost any how.

闵可夫斯基和

Posted on In
Symbols count in article: 2.7k Reading time ≈ 2 mins.

递归式学习

闵可夫斯基和

定义

比较严谨的定义：两个图形 $A, B$ 的闵可夫斯基和 $C = \{a + b |a \in A, b \in B \}$

我的李姐：对于图形 $A$ 中每个点和图形 $B$ 中每个点两两求和（ $(x_a, y_a) + (x_b, y_b) = (x_a + x_b, y_a + y_b)$ ）

盗张图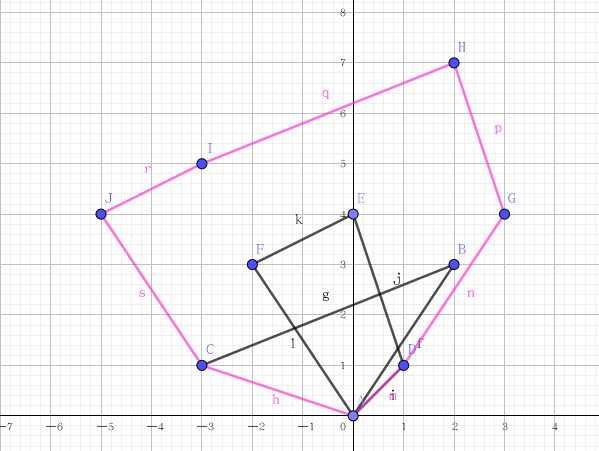：闵可夫斯基和

粉色区域是三角形和一个不规则四边形的闵可夫斯基和

有啥用

当然说有用我才来递归式学习的了

一般用在求凸包上，就以我学这个东西的目的为例吧（顺便说说凸包有啥用）

比如，我们维护了区间和，区间最大后缀和，区间最大前缀和，区间最大子段和分别取名叫 $sum, lmx, rmx, mx$

现在我们要区间加 $k$ ，怎么维护？最简单的是 $sum$ 就不管了

较难的是 $lmx, rmx$ ，以 $rmx$ 为例（注意它是区间最大前缀和，取名为 $r$ 只是因为它在右子树），我们要维护函数 $y = pre(x) + k * x$ 的最大值，其中 $pre(x)$ 代表 $[l, x]$ 的和（前缀和）；考虑斜率优化，我们将函数化为 $pre(x) = kx + y$ ，就是把 $(x, pre(x))$ 看做是一个个点，把斜率为 $k$ 的直线带入这一个个点中，最大化截距，不难发现这就是在凸包上二分切点，因为此时凸包中的所有点都在直线的一侧，自然是在直线上的点代进去之后截距最大

而最毒瘤的就是 $mx$ 了，仿造上面，写出式子： $y = as(x) + k * x$ ，其中 $as(x)$ 代表长度为 $x$ 的最大子段和，但是，求出 $as(x)$ 是 $n^2$ 的，有救吗？有救

考虑分治，我们关心的就是 $(x, as(x))$ 这个点集构成的凸包，不妨来看看 $mx$ 的推导式（在线段树上用过无数次的那个）： mx[l][r] = max(mx[l][mid], mx[mid + 1][r], lmx[l][mid] + r[mid + 1][r]) ，发现前两个可以直接递归求 $[l, mid]$ 和 $[mid + 1, r]$ 的凸包解决，麻烦的是最后那个求和的式子，不难发现它代表的是“跨过 $mid$ 的区间”

考虑我们要求的是什么，是 $(x, as(x))$ 的凸包，将，每个跨过 $mid$ 的区间化作一个点 $(x, y)$ ， $x$ 代表区间长度， $y$ 代表区间和，就是求这个点集（设为 $C$ ）的凸包

点集大小是 $O(n^2)$ 的，当然不能直接求，设点集 $A = \{(x, y) | x \in [l, mid], y = suf(x)\}$ ，其中 $suf(x)$ 表示区间 $[l, mid]$ 的后缀和；再设 $B = \{(x, y) | x \in [mid + 1, r], y = pre(x)\}$ ，其中 $pre(x)$ 表示区间 $[mid + 1, r]$ 的前缀和；那么， $C = \{(x, y) | x = x_A + x_B, y = y_A + y_B\}$ ，这就是闵可夫斯基和呀

而用闵可夫斯基和，我们可以 $O(n)$ 归并出点集 $C$ 的凸包

做法

那怎么合并呢？再看图（回去翻那张）

我们（baidu得）发现发现新的凸包就是原来的两个凸包的边重新极角排序一边，证明？咕咕咕

于是我们得到了一个很有用的结论，求凸包只需要求原来的凸包，然后在一起重新排序就可以了。

但直接重排有点浪费，由于原来两个凸包都已经求好了，于是可以类似归并排序，重新归并一次

代码

例题就不讲了，我要回溯去递归下一条路径了（dfs式学习，艹）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
struct Point
{
    LL x, y;
    //friend老香了
    IL FR Point operator + (Point x, Point y)
    {
        return {x.x + y.x, x.y + y.y};
    }
    IL FR Point operator - (Point x, Point y)
    {
        return {x.x - y.x, x.y - y.y};
    }
    IL FR bool operator <= (Point x, Point y)
    {
        return x.y * y.x <= x.x * y.y;
    }
} ;
struct Hull
{
    Point *st;
    int top, now;
    IL Point& operator [] (const int& x)
    {
        return st[x];
    }
    IL void ins(const Point& x)
    {
        st[x.x].y = max(st[x.x].y, x.y);
    }
    IL void push_back(const Point& x)
    {
        st[++top] = x;
    }
    IL void prev(int len) //预处理,长度为x的答案对应其位置,方便ins
    {
        for (int i = 1; i <= len; ++i)
            st[i] = {i, -INF};
        top = len;
    }
    IL void convex()
    {
        if (top <= 2)
            return ;
        for (int i = 3, len = top, top = 2; i <= len; ++i)
        {
            if (st[i].y == -INF)
                continue;
            while (top > 1 && (st[top] - st[top - 1]) <= (st[i] - st[top - 1]))
                --top;
            st[++top] = st[i];
        }
        now = 1;
    }
    IL LL maxv()
    {
        while (now != top && (-tag) * (st[now + 1].x - st[now].x) < (st[now + 1].y - st[now].y))
            ++now;
        return tag * st[now].x + st[now].y;
    }
} ;
IL void minkowski(Hull& c, Hull& a, Hull& b)
{
    int i = 1, j = 1;
    c.ins(a[i] + b[j]);
    while (i != a.top && j != b.top)
    {
        (a[i + 1] - a[i]) <= (b[j + 1] - b[j]) ? ++j : ++i;
        c.ins(a[i] + b[j]);
    }
    while (i != a.top)
        c.ins(a[++i] + b[j]);
    while (j != b.top)
        c.ins(a[i] + b[++j]);
}

这个板子优点是快，缺点是指针需要人工分配内存