Dyd's Blog

He who has a strong enough why can bear almost any how.

带花树

Posted on Edited on In
Symbols count in article: 5.5k Reading time ≈ 5 mins.

莫名想到三十六计：树上开花

带花树

Blossom Algorithm

二分图最大匹配

一般用匈牙利算法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
bool bfs(int x)
{
    for (int i = h[x], y; i != -1; i = e[i].ne)
        if (!vis[y = e[i].ver])
        {
            vis[y] = true;
            if (!match[y] || dfs(match[y]))
            {
                match[y] = x;
                return true;
            }
        }
    return false;
}
for (int i = 1; i <= n; ++i) //main里
{
    for (int j = 1; j <= n + m; ++j)
        vis[j] = false;
    if (dfs(i))
        ++ans;
}

时间复杂度是 $O(NM)$ 的

当然也可以网络流，并且网络流一般比匈牙利快，因为它的期望复杂度为 $O(M\sqrt{N})$ （Galil Zvi在论文Efficient Algorithms for Finding Maximal Matching in Graphs中证明）

一般图最大匹配

考虑一下二分图和一般图的最大区别，就是二分图没有奇环，而一般图是可以有的，所以匈牙利算法中的寻找增广路然后路径取反的方法在一般图上就不适用了

主要还是要解决奇环的问题

我们发现一个奇环里至少有一个点不能匹配，即这个点在环内两边的连边都不是匹配边，也只有这个点可以向环外连边，那就干脆把一个奇环缩成一个点（开花），路径取反的时候再暴力展开一个个取反，对原图用bfs找一条增广路，这棵节点可能是花的bfs树就称作带花树

正确性：

设原图为 $G$ ，缩花后图为 $G’$ ，我们只要证明“ $G$ 存在增广路的充要条件是 $G’$ 存在增广路”

看花

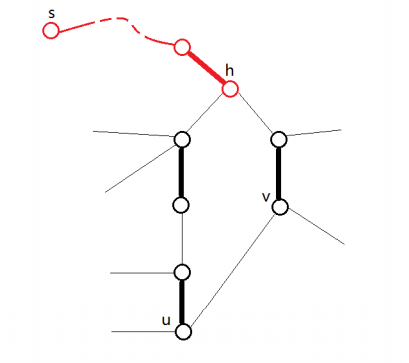
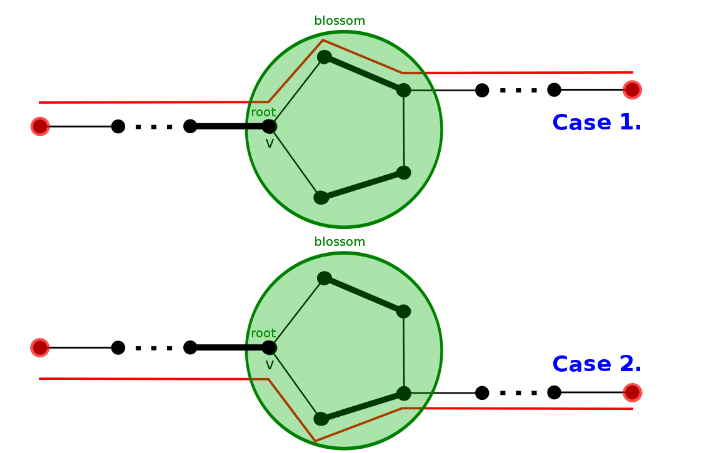
首先要明确带花树的形态，如图，加粗的是匹配边。黑色是一个花上的边，红色是其它边，可以发现，整个花上只有 $h$ 一个非匹配点（这里的“匹配”是指和花内的点），也就只有它可以向外匹配，所以从环外的边出去有两种情况，顺时针或逆时针

出花

可以发现 $G$ 和 $G’$ 的增广路都可以对应

增广

带花树的本质还是寻找增广路

对于每个匹配 $(u \to v)$ 给 $u$ 染绿色， $v$ 染白色

遍历绿点的出边，如果访问到的点未被染色且未被匹配，那么就找到了一条增广路；如果被匹配了，则将该点染白色，将该点的匹配点染绿色并加入队列中

如果访问到的点是白点，那么找到了一个偶环，没有影响无需处理；如果访问到的点是绿点，那么找到了一个奇环，在bfs树上找到这两个点的lca即可定位这个奇环，可以用并查集将其缩起来，因为缩起来的环是一个绿点，所以环上的白点都需改成绿点并加入到队列中，这个缩奇环的操作就是开花

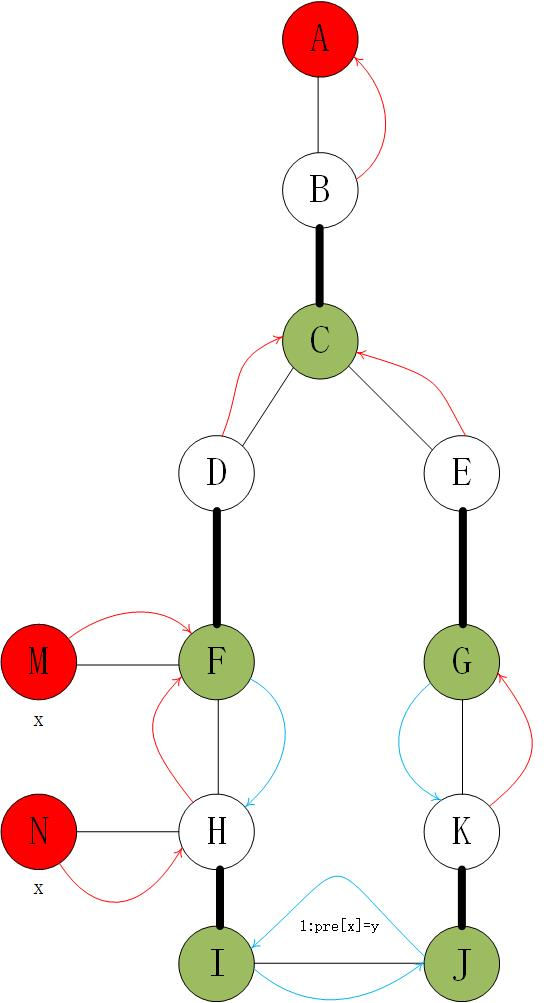
开花

还是对于每个匹配 $(u \to v)$ 给 $u$ 染绿色， $v$ 染白色，花外点表示为红色（它们也可能染了绿/白色），不妨就叫它们 $u$ 型点和 $v$ 型点（这仅是一种不严格的颜色命名，想表达的意思仅仅是“我们的增广从一个 $u$ 型点开始”），那么不难发现，花的根（ $C$ ）一定是 $u$ 型点（这样才有奇环的矛盾）

hh

那么遇到奇环时，一定是存在两个同类型点产生冲突（如 $I, J$ ），带花树算法的处理方法是：将花缩成一点，该点作为u型点向花外遍历，在修改増广路的时候再将花展开（这只是一种理解方式，实现时并不真正进行缩展，而是用并查集模拟缩花的过程，用反向 pre 保证花内部増广路的正确）

首先，我们考虑用一个并查集维护花根之间的关系（因为可能出现花套花的情况），即将花内所有分花根合并到新出现的总花根上（即一直维护一个“极大”的花）

然后处理花内部的増广路关系，这是带花树算法的精髓：

  1. 在产生冲突前，奇数环上所有 $u$ 型点都已进行了从环内向环外的遍历

  2. 产生冲突后，我们分别以冲突的两点为新的出发点（当然是 $u$ 型） ，向对方方向继续染色増广

    可以发现，对方方向上原本的 $v$ 型点，可以作为出点向花外遍历，而这条増广路是从花内距花根较远的一条路延伸来的

  3. 考虑如何记录这条较远的非常规路径。我们知道，在匈牙利算法中，对于每一对匹配中的被匹配点（ $v$ 型点），我们都会有一个 match 指向其前驱匹配节点（ $u$ 型点）（即图中的红色边），也就是说仅有 $v$ 型点具有 pre ；

    然而在花中，所有点可以作为 $u$ 型点向外遍历，也就没有了严格的 $u, v$ 区分，因此无论 $u, v$ 染色情况如何，我们为花中所有匹配对之间建立相互的 pre ，具体实现见下（注意由于原本已有部分 pre ，即红色边，我们要根据特殊性质去建立剩余的 pre ，即蓝色边）

    特别注意，如果到了u为根节点，就不要再反向建立 pre 了，因为它所在匹配对并不完全属于花！

这样，无论以哪个点作为 $u$ 向环外遍历，我们在花内部都能得到正确的増广路

时间

可以发现，通过缩环减少一个点的复杂度为均摊 $O(\log n)$ ，因为使用了并查集。找到一条增广路最坏情况下需要遍历整张图，复杂度为 $O(n + m)$ ，总共就是 $O(n(n \log n + m))$ ，大概就是 $O(nm)$

代码

一般图最大匹配

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
#include <bits/stdc++.h>
#define STC static
using namespace std;

const int N = 1e3 + 5;
int n;
struct Edge
{
    int ne, ver;
} e[N * N];
int h[N], idx = 0, ans = 0;
int match[N], col[N], pre[N];
int fa[N];
queue<int> q;
void link(int x, int y)
{
    match[x] = y, match[y] = x;
}
void add(int x, int y)
{
    e[idx] = {h[x], y}, h[x] = idx++;
}
void dadd(int x, int y)
{
    if (!match[x] && !match[y])
        link(x, y), ++ans;
    add(x, y), add(y, x);
}
void rev(int x)
{
    if (x)
        //奇妙的是,这里可以写成x[pre][match]
        rev(match[pre[x]]), link(x, pre[x]);
}
int find(int x)
{
    return x == fa[x] ? x : fa[x] = find(fa[x]);
}
int lca(int x, int y)
{
    STC int dfn[N], cnt = 0;
    /*
    dfn是一个标记数组,一边打标即一边上跳，第一个重复点就是花根
	花根一定是一个绿点,所以可以隔点上跳
    */
    for (++cnt; ;x = pre[match[x]], swap(x, y))
        if (dfn[x = find(x)] == cnt)
            return x;
        else if (x)
            dfn[x] = cnt;
}
void blossom(int x, int y, int w) //缩奇环(开花)
{
    for (; find(x) != w; x = pre[y])
    {
        pre[x] = y, y = match[x];
        if (col[y] == 2)
            col[y] = 1, q.push(y);
        //这里一定要判一下
        if (find(x) == x)
            fa[x] = w;
        if (find(y) == y)
            fa[y] = w;
    }
}
int aug(int x) //带花树
{
    if ((ans + 1) * 2 > n)
        return 0;
    for (int i = 1; i <= n; ++i)
        fa[i] = i, col[i] = pre[i] = 0;
    while (!q.empty())
        q.pop();
    for (q.push(x), col[x] = 1; !q.empty(); q.pop())
        for (int u = q.front(), i = h[u], v, w; i != -1; i = e[i].ne)
        {
            if (find(u) == find(v = e[i].ver) || col[v] == 2)
                continue;
            if (!col[v])
            {
                col[v] = 2, pre[v] = u;
                if (!match[v])
                    return rev(v), 1;
                col[match[v]] = 1, q.push(match[v]);
            }
            else //缩环两个方向各一次拼起来
                blossom(u, v, w = lca(u, v)), blossom(v, u, w);
        }
    return 0;
}
int main()
{
    int m;
    scanf("%d %d", &n, &m);
    for (int i = 1; i <= n; ++i)
        h[i] = -1;
    for (int x, y; m--; dadd(x, y))
        scanf("%d %d", &x, &y);
    for (int i = 1; i <= n; ++i)
        ans += (!match[i] && aug(i));
    printf("%d\n", ans);
    for (int i = 1; i <= n; ++i)
        printf("%d ", match[i]);
    return 0;
}

随机匹配法

还有一组和智慧法类似的东西，由luogu上皎月半洒花巨佬提出

思路就是随机匹配

发现匹配本质上就是在找增广路，但直接枚举每个点找增广路会有问题，对于一张二分图，一条增广路要么是一条奇链、要么是一条奇链套一个偶环，偶环上总可以完备匹配，所以绕偶数步走到原点并不改变下一条边的匹配状态；但是奇环则未必，如果经过一个奇环，就必然会存在冲突的情况

所以随机匹配的思想就是，不找环，只找长度为奇数的简单路，这样做相当于强制断环为链，正确性难以保证

但是考虑如果多做几次，错误率就会大大下降，于是考虑多做几次这样的匹配

注意到这样做很容易被卡掉，只需要多几个奇环顺便构造一下加边顺序就可以了，所以就可以每次走的时候将边随机一下即可

最后附上花巨的一句话（听不懂但是好装B啊）：“题是众生一般题，水是天下一样水”

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
#include <bits/stdc++.h>
#define STC static
#define DRG default_random_engine
#define DB double
using namespace std;
const int N = 1e3 + 5;
int n, ans;
int match[N], vis[N];
//clock_t 就是 long
clock_t st;
DRG drg{20051221};
vector<int> e[N];
DB when()
{
    return (DB)(clock() - st) / CLOCKS_PER_SEC;
}
void add(int x, int y)
{
    e[x].push_back(y);
}
void dadd(int x, int y)
{
    add(x, y), add(y, x);
}
void link(int x, int y)
{
    match[x] = y, match[y] = x;
}
int work(int x)
{
    shuffle(e[x].begin(), e[x].end(), drg);
    vis[x] = 1;
    for (auto y : e[x])
        if (!match[y])
            return link(x, y), vis[y] = 1;
    for (auto y : e[x])
    {
        int z = match[y];
        if (vis[z])
            continue;
        link(x, y), match[z] = 0;
        if (work(z))
            return 1;
        link(y, z), match[x] = 0;
    }
    return 0;
}
int main()
{
    int m;
    scanf("%d %d", &n, &m);
    for (int x, y; m--; dadd(x, y))
        scanf("%d %d", &x, &y);
    st = clock();
    while (when() < 0.9)
        for (int i = 1; i <= n; ++i)
            if (!match[i])
            {
                fill(vis + 1, vis + 1 + n, 0);
                ans += work(i);
            }
    printf("%d\n", ans);
    for (int i = 1; i <= n; ++i)
        printf("%d ", match[i]);
    return 0;
}

如果是一般的出题人，也就认了，但是这个总有毒瘤搞不清立场，帮出题人造hack，对此广大网友评价为：“卡 随 机 的 艺 术”

但有什么办法呢，人家是大佬（反正我带花树过了）