又一个奇怪的树
圆方树
圆方树(Block forest)是一种树的结构,它能轻松的将仙人掌转化为树,并支持一些操作,有时我们也可以在一般无向图上使用它
定义
先明确一些基本定义:
- 仙人掌:每条边在不超过一个简单环中的无向图
- 点双连通分量:图中任意两不同点之间都有至少两条点不重复的路径
要构造圆方树,当然是要构造出圆点和方点,圆点比较简单,直接保留仙人掌上的点即可;然后对仙人掌进行点双 $Tarjan$ 缩点,每一个点双就是一个方点
对于边,原图上的边统一不要,直接从所以方点向它对应的点双包括的圆点连边,这样,每一个点双就形成了以方点为根,圆点为叶的“菊花图”,而这很多个“菊花图”通过原图中的割点连接在一起(因为点双的分隔点是割点),如图:
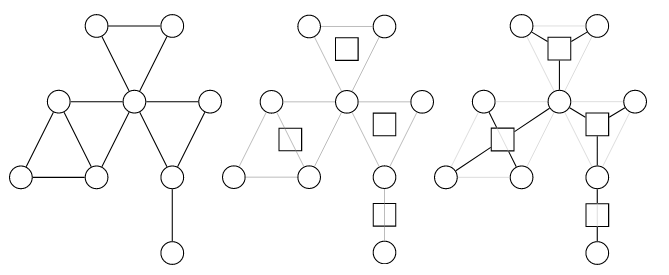
圆方树的点数小于 $2n$ ,所以请注意各种数组大小要开两倍
其实,如果原图连通,则“圆方树”才是一棵树,如果原图有 $k$ 个连通分量,则它的圆方树也会形成 $k$ 棵树形成的森林
如果原图中某个连通分量只有一个点,则需要具体情况具体分析,我们在后续讨论中不考虑孤立点
构造
直接对原图进行 $Tarjan$ ,因为原图上每个环都是一个点双,而且在栈中的顺序就是环上点的顺序,如果一个点 $i$ 的出边 $(i, j)$ 满足 $dfn(i) < low(j)$ ,说明 $(i, j)$ 是一条树边,直接加上即可;如果 $dfn(i) = low(j)$ ,那么我们找到了一个环(可能是重边造成的二元环),则从栈中取出点直到取出 $j$ 为止,设这样从栈中取出的点集为 $R$ ,则 $i$ 和 $R$ 构成一个环
对于环,我们新建一个方点,对环上每个点连边即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
| #include <bits/stdc++.h>
#define STC static
using namespace std;
const int N = 1e5 + 5;
vector<int> G[N], T[N * 2];
int n, m, cnt;
int stk[N], top;
int dfn[N], low[N], dfc = 0;
void tarjan(int x)
{
low[x] = dfn[x] = ++dfc;
stk[++top] = x;
for (auto y : G[x])
if (!dfn[y])
{
tarjan(y);
low[x] = min(low[x], low[y]);
if (low[y] == dfn[x])
{
++cnt;
for (int z = 0; z != y; --top)
{
z = stk[top];
T[cnt].push_back(z);
T[z].push_back(cnt);
}
T[cnt].push_back(x);
T[x].push_back(cnt);
}
}
else
low[x] = min(low[x], dfn[y]);
}
int main()
{
scanf("%d %d", &n, &m);
cnt = n;
for (int i = 1, u, v; i <= m; ++i)
{
scanf("%d %d", &u, &v);
G[u].push_back(v);
G[v].push_back(u);
}
for (int i = 1; i <= n; ++i)
if (!dfn[i])
tarjan(i), --top;
cout << endl << endl;
for (int i = 1; i <= cnt; ++i)
{
for (auto j : T[i])
{
cout << i << " " << j << endl;
}
}
return 0;
}
|
性质
圆方树有优美的性质:
- 无论如何换根,圆方树形态不变,因为你是把环连成菊花而不是别的什么
- 圆方树的子树 = 原仙人掌的子仙人掌,分类讨论各种情况可以证明
- 方点不会和方点相连
还有其他神奇的性质,要具体题目具体分析
一些应用
下面开始口胡
仙人掌最短路
类比树上最短路,我们在LCA处考虑,然而圆方树的树上距离并不一定就等于仙人掌上的最短路长度
注意到圆方树中的边权都还没有确定,可以利用,如果一条边是圆圆边(圆点指向圆点的边,这里已经任意选择一圆点为根),那么它是一个树边,边权等于原仙人掌上边权;如果是方圆边,那么边权等于环的根到那个圆点的最短路径长度;如果是圆方边,那么边权为 $0$
这样,如果一对询问点在圆方树上的LCA是圆点,那么其圆方树上长度就是原仙人掌上长度,因为路径上唯一的不同就在于对于每个环是走哪一侧(这个决策对每个环是独立的),而前面边权的确定已经解决了这一问题;
如果LCA是方点,则我们只需要考虑在LCA这个环中是否要走经过根的那一侧,需要找出这两个询问点 $(x, y)$ 分别是在这个方点的哪两个儿子 $(px, py)$ 的子树中,求同一个环上的点 的最短路径(其实也就是走哪一侧的问题 )可以先记录环上边权的前缀和,这样就能 $O(1)$ 计算出不经过根那条路径的长度,再通过记录整个环的边权和比较出走哪一侧更优
仙人掌dp
仙人掌有若干种DP,比如最大独立集和直径
最大独立集比较简单,只需要DFS时,树边按照树上独立集的方式转移,环上用一个 f[i][0/1][0/1] 的简单DP去转移即可
求直径的话,我们类比求树直径的方式,在LCA处考虑,设 f[i][1/2] 为 $i$ 子树中的第 $j$ 深的点,那么圆点可以轻松转移、更新答案;在方点转移也容易,但更新答案不能直接更新(因为有哪一侧的问题,直接取不一定是最短路,会导致答案偏大),我们可以把环复制一份用单调队列来解决,也可以正反各做一次前缀和
等等
算了,反正我也不会,看这个吧
例题
还是给道题:
战略游戏
这是一道图上圆方树
先建出圆方树,则要求删掉多少个圆点后 $S$ 在圆方树上对应的圆点不全连通,这就是连通子图中的圆点个数减去 $|S|$ ,或者说,圆方树上 $S$ 中节点两两间路径(树上只有唯一路径)的点集并减去 $S$
如何计算连通子图中的圆点个数?有一个方法:
把圆点的权值放到它和它的父亲方点的边上,问题转化为求边权和,即把 $S$ 中的点按照DFS序排序,计算排序后相邻两点的距离和(还包括首尾两点之间的距离),答案就是距离和的一半,因为每条边只被经过两次
最后,如果子图中的深度最浅的节点是圆点,答案还要加上 $1$ ,因为我们没有统计到它
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
| #include <bits/stdc++.h>
#define STC static
using namespace std;
const int N = 1e5 + 5, D = 25;
vector<int> G[N], T[N << 1];
int n, m, cnt, q;
int stk[N], top;
int dfn[N << 1], low[N], dfc = 0;
int dep[N << 1], f[N << 1][D + 5], dis[N << 1];
void tarjan(int x)
{
low[x] = dfn[x] = ++dfc;
stk[++top] = x;
for (auto y : G[x])
if (!dfn[y])
{
tarjan(y);
low[x] = min(low[x], low[y]);
if (low[y] == dfn[x])
{
++cnt;
for (int z = 0; z != y; --top)
{
z = stk[top];
T[cnt].push_back(z);
T[z].push_back(cnt);
}
T[cnt].push_back(x);
T[x].push_back(cnt);
}
}
else
low[x] = min(low[x], dfn[y]);
}
bool cmp(int x, int y)
{
return dfn[x] < dfn[y];
}
void dfs(int x, int fa)
{
dfn[x] = ++dfc;
dep[x] = dep[f[x][0] = fa] + 1;
dis[x] = dis[fa] + (x <= n);
for (int i = 1; i <= D; ++i)
f[x][i] = f[f[x][i - 1]][i - 1];
for (auto y : T[x])
if (y != fa)
dfs(y, x);
}
int lca(int x, int y)
{
if (dep[x] > dep[y])
swap(x, y);
for (int i = D; i >= 0; --i)
if (dep[f[y][i]] >= dep[x])
y = f[y][i];
if (y == x)
return x;
for (int i = D; i >= 0; --i)
if (f[x][i] != f[y][i])
x = f[x][i], y = f[y][i];
return f[x][0];
}
int main()
{
int TT;
scanf("%d", &TT);
while (TT--)
{
scanf("%d %d", &n, &m);
for (int i = 1; i <= n; ++i)
{
G[i].clear();
dfn[i] = low[i] = 0;
}
for (int i = 1; i <= (n << 1); ++i)
T[i].clear();
for (int i = 1, u, v; i <= m; ++i)
{
scanf("%d %d", &u, &v);
G[u].push_back(v);
G[v].push_back(u);
}
cnt = n;
dfc = 0, tarjan(1), --top;
dfc = 0, dfs(1, 0);
scanf("%d", &q);
while (q--)
{
STC int s, a[N];
scanf("%d", &s);
int ans = s * -2;
for (int i = 1; i <= s; ++i)
scanf("%d", &a[i]);
sort(a + 1, a + 1 + s, cmp);
for (int i = 1; i <= s; ++i)
{
int u = a[i], v = a[i % s + 1];
ans += dis[u] + dis[v] - 2 * dis[lca(u, v)];
}
if (lca(a[1], a[s]) <= n)
ans += 2;
printf("%d\n", ans / 2);
}
}
return 0;
}
|
