Dyd's Blog

He who has a strong enough why can bear almost any how.

李超线段树

Posted on In
Symbols count in article: 3.2k Reading time ≈ 3 mins.

队爷的智慧

李超线段树

问题引入

顾名思义，这是由队爷lc提出的一种线段树，用于维护一下问题：

在平面直角坐标系下维护两个操作：

  1. 在平面上加入一条线段
  2. 查询直线 $x = k$ 与已有线段交点的纵坐标最大的线段的编号（也可以得到最大值）

算法流程

既然是线段树，自然少不了区间和区间信息

lc线段树以值域为区间，对于区间 $[l, r]$ lc线段树维护的信息是“与直线 $x = mid$ 的交点纵坐标最大的线段”

询问很好解决了，只要对所有包含 $k$ 的区间上的线段都计算一下即可

问题在于跟新，如何在加入一条线段后维护出新的最大线段，考虑向节点信息为 $f_1(x) = k_1x + b$ 的区间 $[l, r]$ 插入一条线段 $f_2(x) = k_2x + b$ （保证线段可以覆盖整个区间），分类讨论（下面红色代表 $f_1$ ，蓝色代表 $f_2$ ，绿色代表 $x = mid$ ）：

  1. 两条线段有明确的大小关系，即在区间内一条线段完全大于（小于）另一条，直接跟新即可

    4

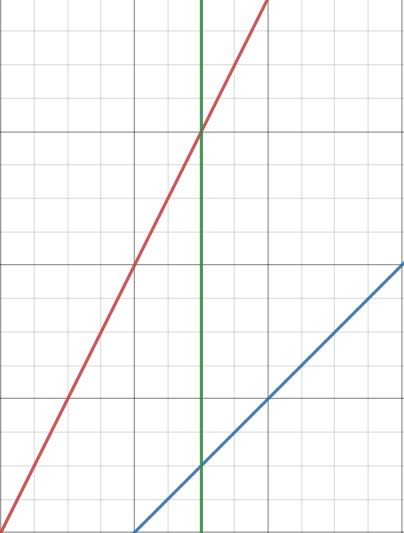
  2. $k_2 > k_1 \wedge f_1(mid) < f_2(mid)$

1

此时用 $f_2$ 跟新当前区间，并用 $f_1$ 跟新左子树（这里有一个类似标记永久化的思想，右子树的信息可能并不是该有的 $f_2$ ，但询问时我们会用 $f_2$ 的答案而不会取右子树的答案）

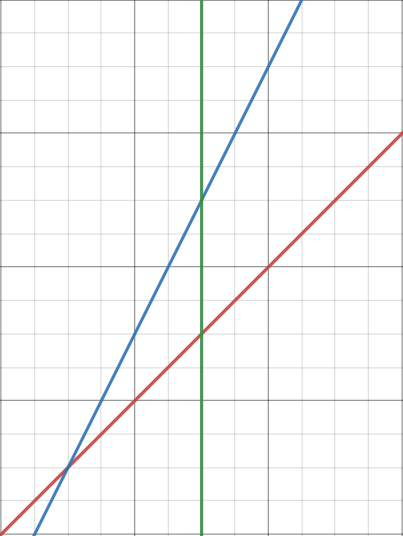
  1. $k_2 < k_1 \wedge f_1(mid) < f_2(mid)$

2

此时用 $f_2$ 跟新当前区间，并用 $f_1$ 跟新右子树

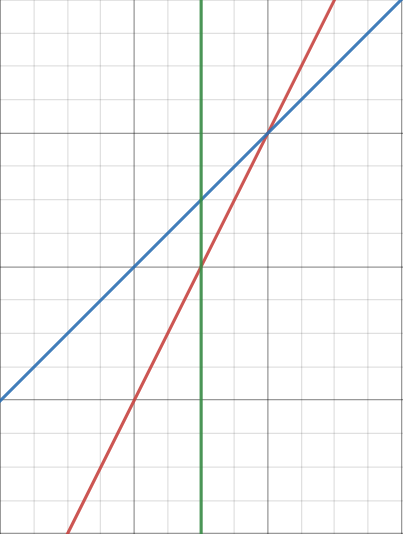
  1. $k_2 > k_1 \wedge f_1(mid) > f_2(mid)$

3

此时用 $f_2$ 跟新右子树，当前区间不变

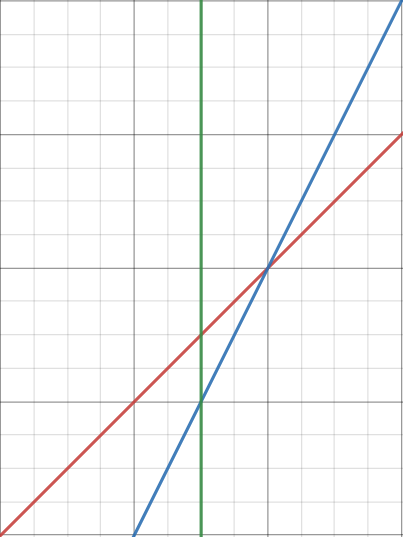
  1. $k_2 < k_1 \wedge f_1(mid) > f_2(mid)$

（懒得放图了）

此时用 $f_2$ 跟新左子树，当前区间不变

lc线段树没有 push_up 和 push_down

有一个需要注意的点是，为了方便求值和交点，我们用斜截式存线段，但垂直于 $x$ 轴的直线没有斜截式

我们考虑到对于垂直于 $x$ 轴的线段 $(x_0, y_1) \to (x_0, y_2), (y1 \le y2)$ ，在只关注最值的情况下，它等效于一个点 $(x_0, y_2)$ ，而点就可以写成 $y = 0x + y_2, (x_0 \le x \le x_0)$ (就是平行于 $x$ 轴的，长度只有一个点的直线)

考虑时间：

询问操作要遍历每一个包含 $k$ 的区间，是 $O(\log n)$ 的，而插入线段操作首先要把这个线段分给若干区间（保证线段一定覆盖区间），这是一个类似区间查询的操作，要 $O(\log n)$ ，而对于每个区间，我们会递归跟新它的儿子，又要一个 $O(\log n)$ 所以插入操作的总时间是 $O(\log^2 n)$ 的

注意上面的 $n$ 指的是值域

代码

板子？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
#include <bits/stdc++.h>
#define DB double
using namespace std;
const int N = 1e5 + 5, P1 = 39989, P2 = 1e9 + 7;
const DB eps = 1e-8, INF = 1e18;
int lastans = 0;
int cmp(DB x, DB y)
{
    if (fabs(x - y) < eps)
        return 0;
    return x > y ? 1 : -1;
}
struct Line
{
    DB k, b, l, r;
    DB clac(DB x)
    {
        if (x > r || x < l)
            return -INF;
        return x * k + b;
    }
} l[N];
struct LineTree
{
    struct Node
    {
        int l, r, id;
    } tr[P1 << 2];
    #define l(x) tr[(x)].l
    #define r(x) tr[(x)].r
    #define id(x) tr[(x)].id
    #define Mid (tr[u].l + tr[u].r >> 1)
    #define lc (u << 1)
    #define rc (u << 1 | 1)
    void build(int u, int l, int r)
    {
        tr[u] = {l, r, 0};
        if (l == r)
            return ;
        int mid = Mid;
        build(lc, l, mid), build(rc, mid + 1, r);
    }
    bool judge(int a, int b, int x)
    {
        DB fa = l[a].clac(x), fb = l[b].clac(x);
        return cmp(fa, fb) ? fa < fb : a > b;
    }
    void update(int u, int l, int r, int d)
    {
        int mid = Mid;
        if (l <= l(u) && r >= r(u))
        {
            //从l18q抄来的优秀打法
            if (judge(id(u), d, mid))
                swap(id(u), d);
            if (judge(id(u), d, l(u)))
                update(lc, l(u), r(u), d);
            if (judge(id(u), d, r(u)))
                update(rc, l(u), r(u), d);
            return ; //记得！
        }
        if (l <= mid)
            update(lc, l, r, d);
        if (r > mid)
            update(rc, l, r, d);
    }
    int ask(int u, int x)
    {
        if (l(u) == r(u))
            return id(u);
        int mid = Mid;
        int res = (x <= mid ? ask(lc, x) : ask(rc, x));
        if (judge(res, id(u), x))
            res = id(u);
        return res;
    }
} lt;
Line get_line(DB a, DB b, DB c, DB d)
{
    if (!cmp(a, c))
        return {0, max(b, d), a, a};
    DB _k = (d - b) / (c - a);
    DB _b = b - (a * _k);
    return {_k, _b, a, c};
}
void get_real(int &x, int P)
{
    x = (x + lastans - 1) % P + 1;
}
int main()
{
    int n, op, a, b, c, d, cnt = 0;
    scanf("%d", &n);
    lt.build(1, 1, 40000);
    while (n--)
    {
        scanf("%d", &op);
        if (!op)
        {
            scanf("%d", &a);
            get_real(a, P1);
            printf("%d\n", lastans = lt.ask(1, a));
        }
        else
        {
            scanf("%d %d %d %d", &a, &b, &c, &d);
            get_real(a, P1), get_real(b, P2), get_real(c, P1), get_real(d, P2);
            if (a > c)
                swap(a, c), swap(b, d);
            l[++cnt] = get_line(a, b, c, d);
            lt.update(1, a, c, cnt);
        }
    }
    return 0;
}