Dyd's Blog

He who has a strong enough why can bear almost any how.

扫描线

Posted on Edited on In
Symbols count in article: 6.9k Reading time ≈ 6 mins.

不只是线段树的那个……

扫描线

普通

虽然线段树那里已经学过一点扫描线了，但还是问一问：

给定一些矩形，求其面积并

这个太简单了，直接跳过了

进阶

看这个：

给定一些三角形，求其面积并

分析

三角形比矩形讨厌的地方在于，矩形平行于坐标轴，只用考虑四个顶点，但三角形可以斜着

考虑把三角形用顶点和交点划分，如图：

三角

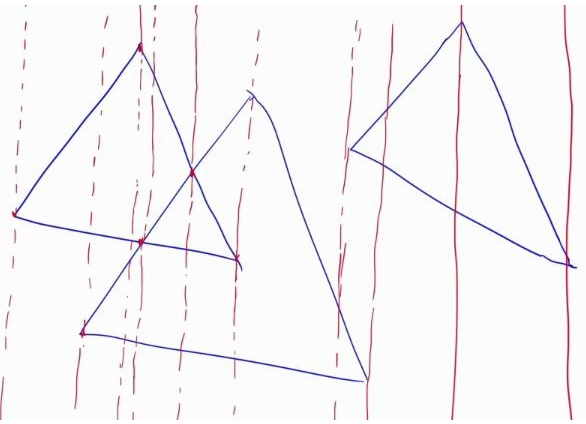
每两个红色的线之间不存在边的交点，换句话说，都是梯形（广义上的），直接两边线段长度求并，乘高除以二即可

由于三角形有 $n$ 个，两两间都可能有交点，故时间复杂度为 $O(N^3)$

注意三角形有边和扫描线重合的特判，排序即可

代码

三角形面积并

大量使用 STL 的后果是，不开 O2 TLE 一个点，开了直接飞过去

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
#include <bits/stdc++.h>
#define fi first
#define se second
#define pb emplace_back
using DB = double;
using PDD = std::pair<double, double>;
const int N = 100 + 10;
const DB eps = 1e-8, INF = 0x3f3f3f3f;
std::array<PDD, 3> tr[N];
PDD q[N];
int n, top;
int cmp(DB x, DB y)
{
    if (std::fabs(x - y) < eps) return 0;
    return x > y ? 1 : -1;
}
PDD operator + (PDD x, PDD y){ return {x.fi + y.fi, x.se + y.se}; }
PDD operator - (PDD x, PDD y){ return {x.fi - y.fi, x.se - y.se}; }
PDD operator * (PDD x, DB y){ return {x.fi * y, x.se * y}; }
PDD operator / (PDD x, DB y){ return {x.fi / y, x.se / y}; }
DB operator & (PDD x, PDD y){ return x.fi * y.fi + x.se * y.se; }
DB operator * (PDD x, PDD y){ return x.fi * y.se - x.se * y.fi; }
bool on(PDD p, PDD x, PDD y){ return cmp((p - x) & (p - y), 0) <= 0; }
PDD jiao(PDD x, PDD u, PDD y, PDD v)
{
    if (!cmp(u * v, 0)) return {INF, INF};
    DB t = v * (x - y) / (u * v);
    PDD o = x + u * t;
    if (!on(o, x, x + u) || !on(o, y, y + v)) o = {INF, INF};
    return o;
}
DB bot(DB x, bool side)
{
    top = 0;
    for (int i = 0; i < n; ++i)
    {
        auto t = tr[i];
        if (cmp(t[0].fi, x) > 0 || cmp(t[2].fi, x) < 0) continue;
        if (!cmp(t[0].fi, x) && !cmp(t[1].fi, x))
        {
            if (side) q[top++] = {t[0].se, t[1].se};
            continue;
        }
        if (!cmp(t[1].fi, x) && !cmp(t[2].fi, x))
        {
            if (!side) q[top++] = {t[1].se, t[2].se};
            continue;
        }
        DB d[3];
        int u = 0;
        for (int j = 0; j < 3; ++j)
        {
            PDD o = jiao(t[j], t[(j + 1) % 3] - t[j], {x, -INF}, {0, INF * 2});
            if (cmp(o.fi, INF)) d[u++] = o.se;
        }
        if (!u) continue;
        std::sort(d, d + u);
        q[top++] = {d[0], d[u - 1]};
    }
    if (!top) return 0;
    for (int i = 0; i < top; ++i) if (q[i].fi > q[i].se) std::swap(q[i].fi, q[i].se);
    std::sort(q, q + top);
    DB res = 0, st = q[0].fi, ed = q[0].se;
    for (int i = 1; i < top; ++i)
        if (q[i].fi <= ed) ed = std::max(ed, q[i].se);
        else
        {
            res += ed - st;
            st = q[i].fi, ed = q[i].se;
        }
    res += ed - st;
    return res;
}
DB calc(DB x, DB y){ return (bot(x, true) + bot(y, false)) * (y - x) / 2; }
int main()
{
    scanf("%d", &n);
    std::vector<DB> xs;
    for (int i = 0; i < n; ++i)
    {
        for (int j = 0; j < 3; ++j)
        {
            scanf("%lf %lf", &tr[i][j].fi, &tr[i][j].se);
            xs.pb(tr[i][j].fi);
        }
        std::sort(tr[i].begin(), tr[i].end());
    }
    for (int i = 0; i < n; ++i)
        for (int j = 0; j < i; ++j)
            for (int p = 0; p < 3; ++p)
                for (int q = 0; q < 3; ++q)
                {
                    PDD o = jiao(tr[i][p], tr[i][(p + 1) % 3] - tr[i][p], tr[j][q], tr[j][(q + 1) % 3] - tr[j][q]);
                    if (cmp(o.fi, INF)) xs.pb(o.fi);
                }
    std::sort(xs.begin(), xs.end());
    DB ans = 0;
    for (int i = 0; i + 1 < xs.size(); ++i) if (cmp(xs[i], xs[i + 1])) ans += calc(xs[i], xs[i + 1]);
    printf("%.2lf\n", ans);
    return 0;
}

炼狱

解决了三角形，就相当于解决了所有多边形（剖分成三角性即可），可正当你得意都时候，圆来了

圆咋办？如果扫描线的话那个弧形可不好求，没有办法，为了对付大boss，只好祭出大杀器——自适应辛普森积分

辛普森积分

先看看辛普森积分是神马

顾名思义，这是一种积分方法，来看下面这个函数：

函数

求面积当然是用积分了，但它的解析式又很麻烦，咋办？

辛普森提出一个玄妙的方法：把他近似成一个二次函数

js

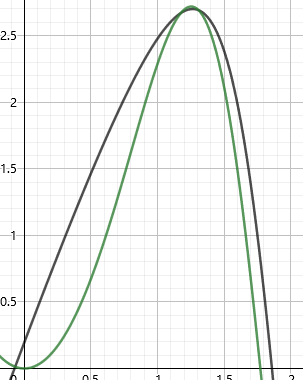
如图，直接把绿色曲线当成黑色的二次函数积分，设绿色曲线为 $y = f(x)$ ，取 $(l, f(l)), (r, f(r)), (mid, f(mid))$ 三个点确定这个黑色的二次函数

二次函数的积分就很好求了，就是：
$$
\frac{f(l) + f(mid) * 4 + f(r)}{6} * (r - l)
$$

自适应

解决了辛普森，来看看自适应

显然直接辛普森积分是无法满足精度要求的，我们要让他“适应”我们设定的精度，具体地，对于区间 $[l, r]$ ，设其辛普森积分后面积为 $S$ ，而区间 $[l, mid], [mid, r]$ 辛普森积分的面积为 $L, R$ ，若 $|L + R - S| < eps$ ，我们就认为这个积分到达了要求的精度；否则，递归积分左右两边，加起来即可

代码

自适应辛普森积分

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include <bits/stdc++.h>
#define DB double
using namespace std;
const DB eps = 1e-12;
DB f(DB x)
{
    return sin(x) / x;
}
DB simpson(DB l, DB r)
{
    return (r - l) * (f(l) + f((l + r) / 2) * 4 + f(r)) / 6;
}
DB asr(DB l, DB r, DB s)
{
    DB mid = (l + r) / 2;
    DB L = simpson(l, mid), R = simpson(mid, r);
    if (fabs(L + R - s) < eps)
        return L + R;
    return asr(l, mid, L) + asr(mid, r, R);
}
int main()
{
    DB l, r;
    scanf("%lf %lf", &l, &r);
    printf("%lf\n", asr(l, r, simpson(l, r)));
    return 0;
}

圆的面积并

辛普森积分的应用一般是更改 f 函数：

圆的面积并

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
#include <bits/stdc++.h>
#define DB double
using namespace std;
const int N = 1000 + 5;
const DB eps = 1e-8;
int n;
struct Point
{
    DB x, y;
    bool operator < (const Point &t) const
    {
        return x == t.x ? y < t.y : x < t.x;
    }
} q[N];
struct Circle
{
    Point p;
    DB r;
} c[N];
int cmp(DB x, DB y)
{
    if (fabs(x - y) < eps)
        return 0;
    return x > y ? 1 : -1;
}
DB f(DB x)
{
    int cnt = 0;
    for (int i = 0; i < n; ++i)
    {
        DB X = fabs(x - c[i].p.x), R = c[i].r;
        if (cmp(X, R) < 0)
        {
            DB Y = sqrt(R * R - X * X);
            q[cnt++] = {c[i].p.y - Y, c[i].p.y + Y};
        }
    }
    if (!cnt)
        return 0;
    sort(q, q + cnt);
    DB res = 0, st = q[0].x, ed = q[0].y;
    for (int i = 1; i < cnt; i++)
        if (q[i].x <= ed)
            ed = max(ed, q[i].y);
        else
        {
            res += ed - st;
            st = q[i].x, ed = q[i].y;
        }
    return res + ed - st;
}
DB simpson(DB l, DB r)
{
    return (r - l) * (f(l) + f((l + r) / 2) * 4 + f(r)) / 6;
}
DB asr(DB l, DB r, DB s)
{
    DB mid = (l + r) / 2;
    DB L = simpson(l, mid), R = simpson(mid, r);
    if (fabs(L + R - s) < eps)
        return L + R;
    return asr(l, mid, L) + asr(mid, r, R);
}
int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; ++i)
        scanf("%lf %lf %lf", &c[i].p.x, &c[i].p.y, &c[i].r);
    DB l = -2000, r = 2000;
    printf("%.3lf\n", asr(l, r, simpson(l, r)));
    return 0;
}

再看一道题

上面两道是以前做的，码风略差，来看这个：

【模板】自适应辛普森法 2

一看，这个函数没法直接积分（不像模板1可以硬艹），就只有自适应辛普森，好消息是显然 $x \to \infty$ 时函数值趋近于 $0$ ，但一个问题是，何时此函数发散？

结论是： $a < 0$ 时，原函数发散

什么，推倒？小小年纪不学好天天就想着推倒别人！啥，还要看推倒过程！你你你，这在我国是违法的啊！

呃呃，还是给大家 推倒 推导一下

首首先，随便去网上找一个收敛准则：

极限比较判别法 ：

对于正项级数 $\{a_n\}, \{b_n\}$ ，有 $\lim_{n \to \infty} \frac{a_n}{b_n} = c$ ：

  1. 若 $c = \infty$ 且 $\sum b_n$ 发散，则 $\sum a_n$ 发散
  2. 若 $c = 0$ 且 $\sum b_n$ 收敛，则 $\sum a_n$ 收敛
  3. 若 $c$ 为常数，则 $\sum a_n$ ， $\sum b_n$ 同时收敛或发散

然后我们来看这个东西，假设原积分在 $x_0$ 处发散（以下 $\int$ 都不写范围）
$$
\begin{aligned}
& \lim_{x \to x_0} \frac{x^{\frac{a}{x} - x}}{x} \\
= & \lim_{x \to x_0} x^{\frac{a}{x} - x - 1} \\
= & \lim_{x \to x_0} e^{\frac{a}{x} - x - 1 \ln x} \\
= & e^{\lim_{x \to x_0} \frac{a}{x} - x - 1 \ln x} \\
\end{aligned}
$$
显然 $\int x$ 是发散的，我们想让 $\int x^{\frac{a}{x} - x}$ 发散，那么就要上式 $= \infty$ ，而如果 $x \to \infty$ （显然 $x \ge 0$ ），那么无论 $a$ 如何取上式都为 $0$ ；所以为了让上式 $= \infty$ ， $x \to 0$ ，此时如果 $a < 0$ 则上式 $= \infty$ ，由极限比较判别法可知， $\int x^{\frac{a}{x} - x}$ 发散

什么？你还想推倒收敛？色胆包天，我我我，我要报警了

开玩笑，下面 推倒 推导 $a \ge 0$ 时必收敛，其实差不多

还是上面的法则：
$$
\begin{aligned}
& \lim_{x \to x_0} \frac{x^{\frac{a}{x} - x}}{\frac{1}{x}} \\
= & e^{\lim_{x \to x_0} \frac{a}{x} - x + 1 \ln x} \\
\end{aligned}
$$
然后就不用我多说了吧？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include <bits/stdc++.h>
using DB = double;
const DB eps = 1e-8;
DB a;
DB f(DB x){ return std::pow(x, a / x - x); }
DB sim(DB l, DB r){ return (r - l) * (f(l) + f((l + r) / 2) * 4 + f(r)) / 6; }
DB asr(DB l, DB r, DB s)
{
    DB mid = (l + r) / 2, t;
    DB ls = sim(l, mid), rs = sim(mid, r);
    if (std::fabs(t = (ls + rs - s)) <= eps * 15) return ls + rs + t / 15;
    return asr(l, mid, ls) + asr(mid, r, rs);
}
int main()
{
    scanf("%lf", &a);
    if (a < 0) puts("orz");
    else printf("%.5lf\n", asr(eps, 20, sim(eps, 20)));
    return 0;
}

然后你会想问 $11$ 行是个啥玩意？其实这是一个公式：
$$
\mid \int_a^b f(x)dx - S(a_1, b_1) - S(a_2, b_2) \mid \approx \frac{1}{15} \mid S(a_1, b_1) + S(a_2, b_2) - S(a, b) \mid
$$