“这不显然吗”
计算几何基础知识
浮点数
$\pi = \arccos(-1)$
余弦定理:$\triangle ABC$ 中 $c^2 = a^2 + b^2 - 2 a b \cos C$
浮点数比较:
1
2
3
4
5
6int cmp(double x, double y)
{
if (fabs(x - y) < eps)
return 0;
return x > y ? 1 : -1;
}判断一个浮点数的符号就是
cmp(x, 0)
向量
如果不清楚可以看这个
向量的表示:一般用点 $(x, y)$ 表示向量 $(0, 0) \to (x, y)$ (把起点平移到原点)
加减法:已知 $\vec{a} = (x_a, y_a), \vec{b} = (x_b, y_b)$ ,则有 $\vec{a} \pm \vec{b} = (x_a \pm x_b, y_a \pm y_b)$ ,其几何意义就是平行四边形定则
数乘:已知 $\vec{a} = (x, y)$ 和标量 $b$ ,则 $b\vec{a} = (bx, by)$
模:向量的长度,定义为已知 $\vec{a} = (x, y)$ ,则模为 $|\vec{a}| = \sqrt{x^2 + y^2}$ ,模长是标量,代码中模长用内积来求
1
2
3
4double mo(Point x)
{
return sqrt(x & x);
}内积(点积):一个向量在另一个向量上的投影长度乘上另一个向量的长度,即已知 $\vec{a} = (x_a, y_a), \vec{b} = (x_b, y_b)$ ,则 $\vec{a} \cdot \vec{b} = |a| |b| \cos<\vec{a}, \vec{b}> = x_a x_b + y_a y_b$ ,是标量
1
2
3
4double operator & (Point x, Point y)
{
return x.x * y.x + x.y * y.y;
}外积(叉积):两个向量围成的平行四边形面积,定义为 $\vec{a} \times \vec{b} = |a| |b| \sin<\vec{a}, \vec{b}>$ ,是向量,方向用右手定则判定,四指从始向量指向末向量,大拇指朝上(朝自己)是正
1
2
3
4double operator * (Point x, Point y)
{
return x.x * y.y - y.x * x.y;
}计算向量夹角
1
2
3
4double angle(Point x, Point y)
{
return acos((x & x) / mo(x) / mo(y));
}向量(点)顺时针旋转角度:
1
2
3
4Point rot(Point x, double theta)
{
return {x.x * cos(theta) + x.y * sin(theta), -x.x * sin(theta) + x.y * cos(theta)};
}计算向量 $\vec{AB}, \vec{AC}$ 围成的平行四边形面积:
1
2
3
4double area(Point x, Point y, Point z)
{
return cross(y - x, z - x);
}
点与线
注意下面的 Point 有些表示点,有些表示向量
直线的表示:
- 一般式: $l : Ax + By + C = 0$
- 斜截式: $l : y = kx + b$
- 点向式: $l: p_0 + t\vec{v}$
- 两点式:不多说,两点定一条直线
一般使用点向式或两点式
判断点于直线关系:
设点 $C$ 与直线 $AB$ ,令 $\vec{v} = \vec{AB} \times \vec{AC}$
左侧: $\vec{v} > 0$
右侧: $\vec{v} < 0$
线上: $\vec{v} = 0$
直线交点,直接上代码了,证明可以考虑平移至共起点后用几何意义:
1
2
3
4
5
6
7Point jiao(Point p, Point u, Point q, Point v)
{
if (u * v == 0) //平行或者重合
return {INF, INF};
double t = (p - q) * v / (u * w);
return p + u * t;
}点到直线距离:
1
2
3
4
5double dis_z(Point p, Point x, Point y) //p到直线(x->y)的距离
{
Point u = y - x, v = p - x;
return fabs((u * v) / mo(u));
}点到线段的距离:
1
2
3
4
5
6
7
8
9
10
11double dis_x(Point p, Point x, Point y)
{
if (x == y)
return mo(p - x);
Point u = y - x, v = p - x, w = p - y;
if (cmp(u & v, 0) < 0)
return mo(v);
if (cmp(u & w, 0) > 0)
return mo(w);
return dis_z(p, x, y);
}点在直线上的投影:
1
2
3
4
5double proj(Point p, Point x, Point y)
{
Point u = y - x;
return x + u * (u & (p - x)) / (u & u));
}判断点是否在直线上:
1
2
3
4bool is_on(Point p, Point x, Point y)
{
return !cmp((p - x) * (p - y), 0) && cmp((p - x) & (p - y), 0) <= 0;
}判断两线段是否相交:
1
2
3
4
5
6bool is_jiao(Point x_1, Point y_1, Point x_2, Point y_2)
{
double c1 = cross(y_1 - x_1, x_2 - x_1), c2 = cross(y_1 - x_1, y_2 - x_1);
double c3 = cross(y_2 - x_2, y_1 - x_2), c4 = cross(y_2 - x_2, x_1 - x_2);
return cmp(c1, 0) * cmp(c2, 0) <= 0 && cmp(c3, 0) * cmp(c4, 0) <= 0;
}
三角形
海伦公式
四心:
- 外心,外接圆圆心,三边中垂线交点,到三角形三个顶点的距离相等
- 内心,内切圆圆心,角平分线交点,到三边距离相等
- 垂心,三条垂线交点
- 重心,三条中线交点(到三角形三顶点距离的平方和最小的点,三角形内到三边距离之积最大的点)
多边形
通常按逆时针存储所有点
凸多边形:
过多边形的任意一边做一条直线,如果其他各个顶点都在这条直线的同侧,则把这个多边形叫做凸多边形,任意凸多边形外角和均为 $360$ 度,任意凸多边形内角和为 $(n−2) 180$ 度
求多边形面积(不一定是凸多边形):
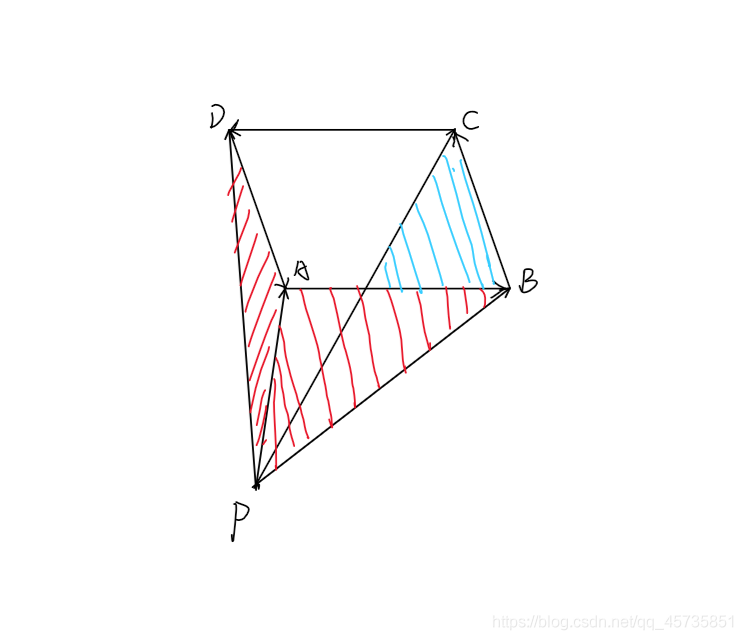
考虑在平面上任取一原点(一般取第一个点),对于边每条边 $AB$ (逆时针储存),计算 $\vec{OA} \times \vec{OB}$ (注意外积是有向的),求和即可,可画图理解
1
2
3
4
5
6
7double pgarea(Point p[], int n) //polygon area
{
double res = 0;
for (int i = 1; i < n - 1; ++i) //这里点编号为0~n-1
res += (p[i] - p[0]) * (p[i + 1] - p[0]);
return res / 2;
}判断点是否在多边形内(不一定是凸多边形):
- 射线法,从该点任意做一条和所有边都不平行的射线,交点个数为偶数,则在多边形外,为奇数,则在多边形内
- 转角法
判断点是否在凸多边形内,只需判断点是否在所有边的左边(逆时针存储多边形)
皮克定理:
皮克定理是指,一个计算点阵中顶点在格点上的多边形面积公式,该公式可以表示为 $S = a + \frac{b}{2} - 1$ ,其中 $a$ 表示多边形内部的点数, $b$ 表示多边形边界上的点数, $S$ 表示多边形的面积
圆
解方程即可
三维
三维的向量表示 $(x, y, z)$
三维向量的加减法、数乘运算、点积运算,都与二维的相同,直接套
向量的模 $|\vec{V}| = \sqrt{x^2 + y^2 + z^2}$
叉积: $\vec{a} \times \vec{b}$ 是一个即垂直于 $\vec{a}$ 也垂直于 $\vec{b}$ 的向量,方向也用右手定则,代数式为 $\vec{a} \times \vec{b} = (y_az_b - y_bz_a, x_bz_a - x_az_b, x_ay_b - x_by_a)$
求法向量:
根据叉积的性质,在平面里找两个不共线的向量,求他俩的叉积就是平面的法向量
判定点是否在平面上:
先求出法向量 $n$ ,然后在平面里任取一点 $p$ ,判断 $(p \to x) * n$ 若为 $0$ 即在平面里
求点到平面的距离:
先求出法向量 $n$ ,然后在平面里任取一点 $p$ , $(p \to x)$ 在 $n$ 上的投影即为距离
$D = \frac{\vec{px} * \vec{n}}{|n|}$
多面题欧拉定理:
多面体的顶点数 - 棱长数 + 表面数 = $2$
例题一
很简单的例题,直接二分每个点在那两个向量之间即可
判断点是否在直线左侧即可
1 |
|
例题二
首先题目可以转化为,求一条过所有线段的直线
考虑枚举每条线段的端点,可以证明,如果存在这样的直线,必然有一条是穿过线段端点中的两个的
证明如下:
假设有一条直线符合题意,现在设其与线段 $l_1$ 的交点为 $A$ ,将直线绕 $A$ 旋转至“即将”不满足题意,此时其必过某条线段端点,再绕该端点旋转一次即可
时间复杂度 $O(Tn^3)$ 在答案为 $YES!$ 的情况下跑不满
1 |
|