自动机/鸡/姬，到底那个好

后缀自动机

定义

后缀自动机（SAM）是一个状态机，他有一个起点，若干终点，原串的所有本质不同子串和从SAM起点开始的所有路径一一对应，不重不漏，所以终点就是包含后缀的点

简单来说就是用一个边上有字符的DAG存储下了一个字符串的所有子串（当然Trie也可以做到，但是Trie的点数和边数都是 $O(n^2)$ 而SAM的点数和边数都是 $O(n)$ 的）

一些性质

再继续讨论SAM前，我们必须先知道一些东西

endpos

定义函数 $endpos(S)$ 表示子串 $S$ 在原串中出现的位置的尾字母下标集合，如对于字符串“abcbabc”，有 $endpos(ab) = \{2, 6\}$

endpos有以下结论（较常用）：

1. 对于两个子串 $s_1, s_2$ ，有：
   $$
   \begin{aligned}
   & s_1是s_2的后缀 \Leftrightarrow endpos(s_2) \subseteq endpos(s_1) \\
   & s_1不是是s_2的后缀 \Leftrightarrow endpos(s_2) \wedge endpos(s_1) = \phi \\
   \end{aligned}
   $$
   正确性可以感性理解一下

2. 两个不同子串的endpos，要么有包含关系，要么没有交集，可以理解为，它们要么有后缀关系，要么没有

对于endpos相同的子串，我们将它们归为一个endpos等价类，对于任意一个endpos等价类，将包含在其中的所有子串依长度从大到小排序，则每一个子串的长度均为上一个子串的长度减1，且为上一个子串的后缀（简单来说，一个endpos等价类内的串的长度连续）

定义 $longest(st), shortest(st)$ ，表示endpos等价类 $st$ 中最长，最短的子串，由以上定义可知：对于 $longest(st)$ 的任意后缀 $s$ ，如果 $| shortest(st) | \le | s | \le | longsest(st) |$ ，则 $s \in st$

而我们还有一个结论：

endpos等价类个数的级别为 $O(n)$

对于一个类（endpos等价类） $st$ ，在 $longest(st)$ 前添加任意一个字符（满足新形成的字符串为原串子串），得到的字符串必然不属于此类，因此会得到若干个新的类，得到新形成的字符串的endpos必然为 $endpos(longest(st))$ 的子集，并且分别添加两个不同的字符，所得到的两个字符串的endpos必然完全不相交，所以对于此操作（添加一个字符），我们可以认为是对一个原集合进行分割，分割得到几个新的集合，且保留原集合，新的集合还可以继续分割，但是总的分割的次数不会超过原集合的大小，所以最终形成的集合个数也不会超过 $2n$

parent tree

考虑上面类的划分过程，将一个串前面添加字符，得到新的类，这种关系可以构成一棵树，如对于串“aababa”（图中红色串为每个类的最长串）：

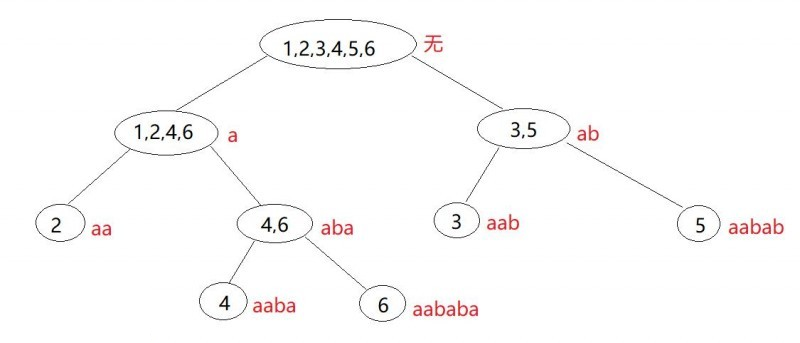
于是，类之间就有了父子关系，我们称这棵树为parent tree，记类 $a$ 的父节点为 $fa(a)$

也有个结论：
$$
|longest(fa(a))| + 1 = |shortest(a)|
$$
正确性很显然，从建树的步骤中就可以看出，在一个类中的最长子串前再添加一个字符，形成的字符串就必然属于其儿子中的一类，且这个新形成的字符串肯定是它所属的类中最短的一个，所以我们只需储存 $|longest(a)|$

那么定义那么多有什么用呢？其实，SAM的节点就是parent tree中的节点，只不过二者的边不同，其中空串所属的节点（parent tree的根）就是后缀自动机的源点，而最大子串（整个原串）所属于的节点，以及其在parent tree上的祖先就是终点，如图即是一个SAM，蓝色为SAM的边，橘色为终点：

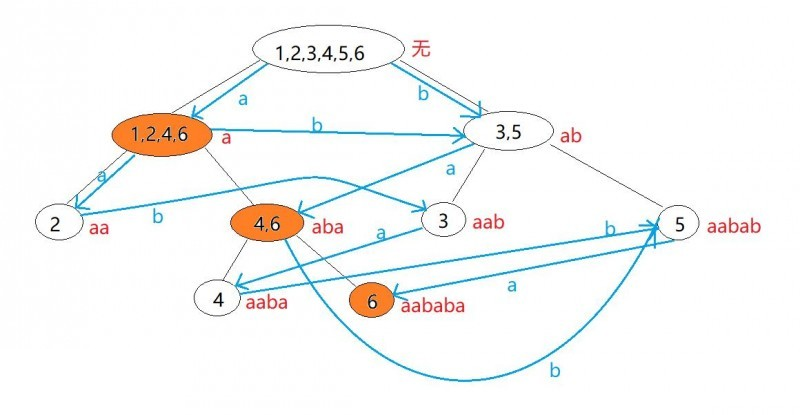
根据定义，SAM的边应该满足：从源点出发到达点 $i$ 的任意一条路径形成的字符串均属于节点 $i$ 所代表的类

二者边的主要区别为，延parent tree的边往下走是在字符串前面添加字符，延自动机的边往下走是在字符串后面添加字符，故parent tree主要用来求节点（即各个字符串）的性质，而后缀自动机本身则主要用来直接跑字符串

数量级

前面证过，SAM的点数为 $O(n)$

下面证明：SAM的边数为 $O(n)$

先取后缀自动机的任意一棵生成树（不是parent tree），这棵树一定与点数同级，即 $O(n)$ ，那么我们考虑向这棵生成树中加边

对于每个终止节点，我们按一定顺序跑遍属于它的子串（跑的时候逆着边的方向），如果能顺利跑回源点，则跑下一个子串；否则，说明我们需要加边，每次连上本应该跑回的边，沿它跑回下一个节点（这里若干次加边后得到一条回源点的路可能不是对于的当前串，但没关系，因为它一定对于终点的某一个子串，我们下次跑那个子串的时候就不必加边了，之后重跑我们原本希望跑的子串，直到真正顺利跑完这个子串）

这样，当跑完所有终止节点时，在原本的生成树上增加的边不会超过后缀的个数，即 $n$ 个，故总的边数是 $O(n)$ 级的

构造

那么如何构造SAM呢？

先看看构造好的长啥样（这个SAM比较特殊，只有一个终点）：

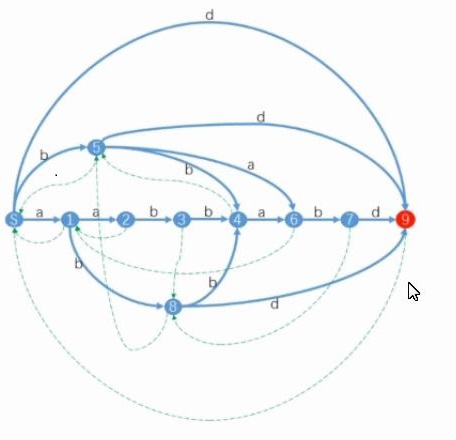
那整齐的一行节点表示的就是各个前缀所属的节点，显然，对于任意一个前缀，它在它所属的类中长度是最长的（不能再在其前面添加字符）

而相邻两个前缀所属点之间也肯定有连边，当然，不相邻的节点之间也会有一些边

上面那些零零散散的节点则是不包含任意一个前缀的节点

而蓝色的边就是SAM中正常的边，绿色的边是parent tree

SAM的构造是在线的，即我们通过不断添加单个字符的方式构建后缀自动机，时刻调整其状态

代码如下：

struct SAM
{
	//1为空节点
	int tot = 1, last = 1; //last:未加入此字符前最长的前缀所属的节点的编号
	//这里的节点只维护了最长的串,因为所有长度小于它但同结尾的串一定被它的祖先维护了
	struct Node
	{
		int len, fa; //最长长度,父节点
		int ch[26]; //类似于Trie
	} nd[N << 1]; //开2倍
	void insert(int x)
	{
		int p = last, np = last = ++tot;
		nd[np].len = nd[p].len + 1;
		for (; p && !nd[p].ch[x]; p = nd[p].fa) //遍历所有长度小于它但同结尾的串,加字符
			nd[p].ch[x] = np;
		/*
		如果最后形成的新字符串没有旧串里出现过,
		说明x实际上是一个在旧串中没有出现过的字符
		因此不可能存在除节点1以外的祖先
		*/
		if (!p)
			nd[np].fa = 1;
		else 
		{
			int q = nd[p].ch[x];
			if (nd[q].len == nd[p].len + 1) //判断np是否为q的子节点
				nd[np].fa = q;
			else //不是就说明q含了不该含的子串,直接新建节点为np的父节点
			{
				int nq = ++tot;
				nd[nq] = nd[q], nd[nq].len = nd[p].len + 1; //这里就相当于去掉不该含的串
				nd[q].fa = nd[np].fa = nq;
				for (; p && nd[p].ch[x] == q; p = nd[p].fa) //同理跟新
					nd[p].ch[x] = nq;
			}
		}
	}
} sam;