神仙数学,一起递归式学的,就写在一起吧
行列式和基尔霍夫矩阵
定义
给定一个无向图 $G(V, E)$
度数矩阵 $D$ :当 $i \ne j$ 时, $D[i][j] = 0$ ,否则 $D[i][j] = 点 i(j) 的度数$
邻接矩阵 $A$ :当 $(u, v) \in E$ 时, $A[u][v] = 1$ ,否则 $A[u][v] = 0$
基尔霍夫矩阵(Kirchhoff) $K$ ,也称拉普拉斯算子:定义为 $K = D - A$ ,如图:
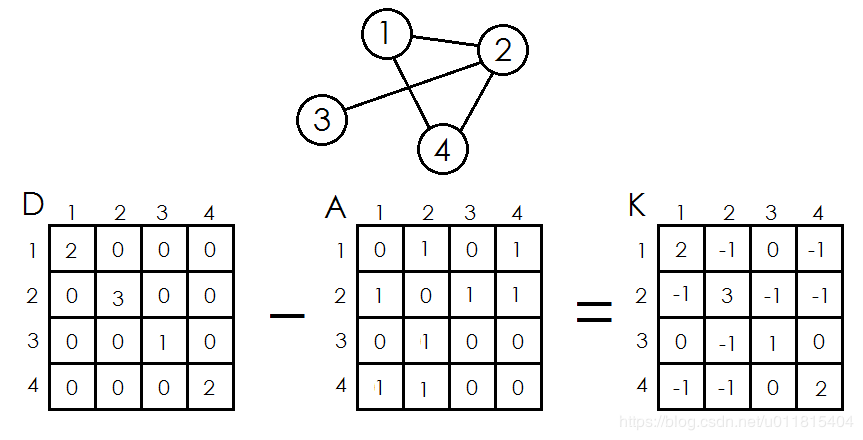
行列式:对于一个 $n \times n$ 的矩阵 $X$ ,其行列式定义为 $\det(X) = \mid X \mid = \sum_{p} (-1)^{\tau(p)} \prod_{i = 1}^n a_{i, p_i}$ ,其中 $p$ 取遍 $1 \sim n$ 的全排列, $\tau(p)$ 表示排列 $p$ 的逆序对个数,行列式可以理解为所有列向量所夹的几何体的有向体积,这样可以结合从几何直观出发理解为线性变换的伸缩因子(没有屁用)
排列的奇偶性:定义排列 $p$ 的奇偶性为 $\tau(p)$ 的奇偶性
对换:交换一个排列 $p$ 中的两个元素 $p_i, p_j (i \ne j)$ ,其它元素不变
行列式
我们来看如何快速求出行列式
关于排列的奇偶性
关于排列的奇偶性,有两个性质:
- 对于 $n(n \ge 2)$ 阶排列的所有排列情况,奇排列和偶排列各占一半
- 一个排列可以通过若干次对换变成一个元素严格递增的自然排列,对换次数的奇偶性与原排列的奇偶性相同
关于行列式的性质
交换对应矩阵的2行(列),行列式取反
交换对应矩阵的1行和1列(进行一次矩阵转置),行列式不变
行列式的行(列)所有元素等比例变化,则行列式也等比例变化,如图:
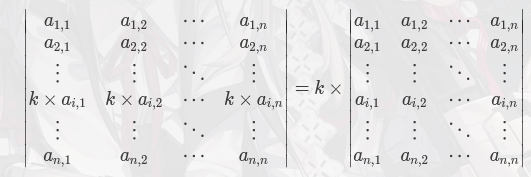
如果行列式对应矩阵 $A$ 中有一行(列),是对应2个矩阵 $B, C$ 中分别的2行(列)所有元素之和,且 $B, C$ 中其它元素都等于 $A$ 中对于元素,则有 $\mid A \mid = \mid B \mid + \mid C \mid$ ,如图:

如果一个矩阵存在两行(列)成比例则 $\mid A \mid = 0$ ,如图:

把一个矩阵的一行(列)的值全部乘一个常数加到另一行(列)上,行列式值不变,如图:
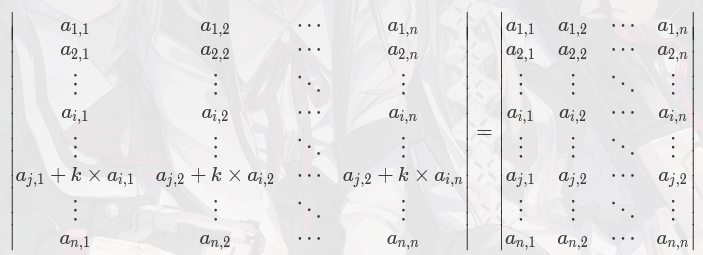
关于代数余子式
由于代数余子式的定义过于复杂,所以在这里定义:
在一个 $n$ 阶行列式 $D$ 中选定 $k$ 行 $k$ 列可以组成一个 **$k$ 阶子行列式 $A$**,而删除在 $k$ 行 $k$ 列后剩下的 $n−k$ 阶行列式称为 $A$ 对应的 $n−k$ 阶余子式 $M$
设 $A$ 在 $D$ 中的下标集合为 $\{ \mathbb{I}, \mathbb{J} \}$ ,其中 $\mathbb{I} = \{i_k\}$ , $\mathbb{J} = \{j_k\}$ ,则定义 $(-1)^{(\sum \mathbb{I})(\sum \mathbb{J})} \times \mid M \mid$ 为 $n$ 阶行列式 $D$ 的 $k$ 阶子式 $A$ 的代数余子式
对于单一元素 $a_{i,j}$ 我们令其代数余子式为 $A_{i,j}$ ,余子式为 $M_{i,j}$ ,有 $A_{i,j}=(-1)^{i+j}M_{i,j}$
那么有如下性质:
$n$ 阶行列式 $D$ 等于其任意一行(列)所有元素与其对应代数余子式的乘积之和,即
$$
\begin{aligned}
D = \sum_{j = 1}^n a_{i, j} \times A_{i, j}, (i \in [1, n]) \\
D = \sum_{i = 1}^n a_{i, j} \times A_{i, j}, (j \in [1, n]) \\
\end{aligned}
$$$n$ 阶行列式 $D$ 的任意一行(列)余另不同的一行(列)对应元素的代数余子式之和为0
$$
\begin{aligned}
\sum_{k = 1}^n a_{i, k} \times A_{j, k} = 0, (i, j \in [1, n] \wedge i \ne j) \\
\sum_{k = 1}^n a_{k, i} \times A_{k, j} = 0, (i, j \in [1, n] \wedge i \ne j) \\
\end{aligned}
$$
以上所有麻烦的要死的性质都不用证明,太好了!
消元
我们考虑一个情况,当一个矩阵任意一个位置出现0,看公式中的 $\prod_{i = 1}^n a_{i, p_i}$ ,发现只有有一个0,整个排列就没有贡献了,所以我们的思路就是利用上面(讨厌至极的)性质,让矩阵中出现0
我们现在考虑将矩阵一行(列)消成只有最后一个元素非0该怎么做,即实现图中变化:
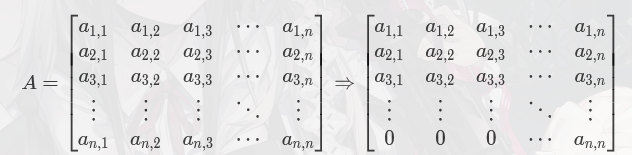
利用行列式的性质6,对于1到第 $n−1$ 列中的第 $i$ 列,我们只需要让第 $i$ 列整列加上第 $n$ 列的 $\frac{a_{n,i}}{a_{n,n}}$ 倍就可以在 $\mid A \mid$ 不变的情况下使得整行前 $n−1$ 个元素被消掉
将最后一行消成只有 $a_{n, n}$ 非0后,由代数余子式的性质1可知 $D = a_{n, n} \times A_{n, n}$ ,其中 $A_{n, n}$ 就是红色矩阵:
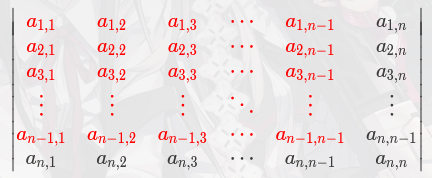
然后我们对于这个红色矩阵 $A_{n, n}$ 又消元,有 $A_{n, n} = a_{n - 1, n - 1} \times A_{n - 1, n - 1}$
如此一直消元下去,得到的就是一个下三角行列式:

我们就会发现这样一个矩阵的行列式是其对角线所有元素的乘积,也就是 $\prod_{i = 1}^n a_{i, i}$
其它细节
- 每次取新的余子式的时候需要注意奇偶性,及时变化正负,因为记得代数余子式是要乘上一个 $(-1)^{(\sum \mathbb{I})(\sum \mathbb{J})}$
- 如果题目要求 $\mod p$ 情况下的行列式,有些数是不一定有逆元的,或者说消元的时候精度出问题,我们可以考虑对两行(列)做辗转相减消元
时间复杂度
消元是 $O(n^3)$ 的,辗转相除法是 $O(\log p)$ 的,因为辗转相除和消元每次必然使得数变小,势能只会减少,所以这个是均摊到 $O(n^2)$ 的(我也不懂为啥),总时间为 $O(n^2\log n + n^3) = O(n^3)$
代码
1 |
|
基尔霍夫矩阵
基尔霍夫矩阵 $K$ 有如下性质:
- 基尔霍夫矩阵的每一行或每一列上的元素和都是0
- 基尔霍夫矩阵的行列式的值为0
- 基尔霍夫矩阵的任意一个代数余子式值都相同
- 如果图 $G$ 不连通,基尔霍夫矩阵 $K$ 的任意主子式行列式值为0
- 如果图 $G$ 是一棵树,基尔霍夫矩阵 $K$ 的任意一个 $n − 1$ 阶主子式的行列式为1
Matrix-Tree 定理
对于已经得出的基尔霍夫矩阵,去掉其第 $k$ 行和第 $k$ 列得出的矩阵的行列式,其绝对值为生成树的个数,该定理被称为Matrix-Tree定理(矩阵树定理)
因此,对于给定的图 $G$ ,若要求其生成树个数,可以先求其基尔霍夫矩阵,然后随意取其任意一个 $n − 1$ 阶行列式,然后求出行列式的值,其绝对值就是这个图中生成树的个数
以上的定理适用于无向无权图无自环的图,下面是一些拓展
加权
如果图中边有边权,可以把度数矩阵 $D$ 变成边的权值和,直接用Matrix-Tree 定理,求得的就是所有生成树边权乘积的总和
有向
首先要把邻接矩阵 $A$ 变成有向图的邻接矩阵,然后对于 $D$ ,如果它记录的是到该点入的边权总和,那么求得的就是外向树 (从根向外),即 $D[i][j] = \sum_{j = 1}^n A[j][i]$ ;类似的,如果它记录的是到该点出的边权总和,那么求得的就是内向树 (从外向根)
关于如何保证根,巨佬们说:去掉第 $k$ 行 $k$ 列就是以 $k$ 为根
代码
1 |
|