Dyd's Blog

He who has a strong enough why can bear almost any how.

左偏树

Posted on Edited on In
Symbols count in article: 4.8k Reading time ≈ 4 mins.

考完学波数据结构

左偏树

左偏树是可并堆的一种，可以在 $O(\log n)$ 的时间内实现堆的合并，它是通过额外维护一个距离并保证性质来实现的（有点类似于点分治找重心）

定义和性质

  • 距离：一个点的距离定义为一个点到离它最近的空节点的距离
  • 性质：每个点的左儿子的距离一定大于等于其右儿子的距离

以上就是左偏树额外维护以保证时间复杂度的信息，不难发现，这棵二叉树（堆）的每个节点的距离一定于右儿子的距离加1

定理：根节点的距离 $dis_{root} \le \log (n + 1)$ ，证明如下：

设 $f(k)$ 表示 $dis_{root} = k$ 的子树至少包含多少点，易得， $f(1) = 1 \le 2^1 - 1$ ，若 $f(k - 1) \le 2^{k - 1} - 1$ ，则对于 $dis_{root} = k$ 的子树，右儿子的距离为 $k - 1$ ，即右子树最少有 $f(k - 1)$ 个点，而左儿子的距离一定大于等于其右儿子的距离，故左子树最少也有 $f(k - 1)$ 个点，则 $f(k) = f(k - 1) + f(k - 1) + 1$ ，即 $f(k) \le 2^k - 1$ ，由数学归纳法原理， $f(k) \le 2^k - 1$ ，则 $f(\log (n + 1)) \le 2^{\log (n + 1)} - 1 = n$ ，可得 $dis_{root} \le \log (n + 1)$

合并

有了以上定义和性质，我们来看看如何合并左偏树，假设我们合并的两个左偏树的根分别为 $a, b$ ，进行如下操作（假设是小根堆）：

  1. 若 $b < a$ ， $swap(a, b)$
  2. 将 $a$ 作为合并后的根节点，并将 $a$ 的左子树作为合并后的左子树
  3. 递归合并 $a$ 的右子树和 $b$ ，将合并后的树作为右子树
  4. 若右子树的距离大于左子树，交换两个子树

可以发现，每一次递归，两个根节点必有一个会变成自己的右子树，即它的距离会减1，当根的距离为1时它就没有右子树了，故时间复杂度为 $O(dis_a - 1 + dis_b - 1) = O(\log (n + 1)) = O(\log n)$

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
struct LeftHeap
{
	int l, r, v, dis;
#define l(x) lh[(x)].l
#define r(x) lh[(x)].r
#define v(x) lh[(x)].v
#define dis(x) lh[(x)].dis
} lh[N];
int merge(int x, int y)
{
    if (!x || !y)
		return x + y;
	if (v(x) > v(y))
		swap(x, y);
	r(x) = merge(r(x), y);
	if (dis(r(x)) > dis(l(x)))
		swap(r(x), l(x));
	dis(x) = dis(r(x)) + 1;
	return x;
}

例题

左偏树的难点主要在于应用

数字序列

约定

先做一个变化：令 $a’_i = a_i - i, b’_i = b_i - i$ ，这样，最小值不会改变，且任意一组解都有唯一的 $\{b’i\}$ 与之对应，而变化的目的是 $b_i < b{i + 1},即b’i + i < b’{i + 1} + i + 1$ ，故 $b’i \le b’{i + 1}$ ，我们把 $<$ 变成了 $\le$ ，为了方便，以下不会再用到原数组，所有的 $\{b_i\}$ 都指的是 $\{b’_i\}$

转化

考虑一个子问题：若有 $n$ 个数 $\{a_i\}$ ，求一个数 $b$ ，使得 $\sum_{i = 1}^n \mid a_i - x \mid$ 最小，即在保证 $b_1 = b_2 = … = b_n = x$ 的情况下求解原问题，明显，取 $\{a_i\}$ 的中位数时最小

那么再考虑，如果有 $n$ 个数 $\{a_i\}$ ，其中对于 $\sum_{i = 1}^m \mid a_i - b_i \mid$ ，其取最小值时 $b_{1 \sim m} = u$ ，对于 $\sum_{i = m + 1}^n \mid a_i - b_i \mid$ ，其取最小值时 $b_{m + 1 \sim n} = v$ ，那么该如何合并 $a_{1 \sim m}$ 和 $a_{m + 1 \sim n}$ 呢？分两类讨论：

  1. 若 $u \le v$ ，即满足 $\{b_i\}$ 的单调性，则两段分别保留自己的 $b$
  2. 若 $u > v$ ，即不满足单调性，则使 $b_{1 \sim n}$ 为 $a_{1 \sim n}$ 的中位数

正确性

第一类正确性很好理解，下面证明第二类做法的正确性（即取中位数后 $\sum_{i = 1}^n \mid a_i - b_i \mid$ 最小）：

设对于 $a_{1 \sim n}$ 的一组最优解为 $\{b_i\} = \{x_i\}$

若 $x_m > u$ ，则由单调性可得 $x_{m + 1 \sim n} > u$ ，由于 $b_{1 \sim m} = u$ 是对于 $a_{1 \sim m}$ 的最优解，所以用 $u$ 替换 $x_{1 \sim m}$ 仍然满足单调性且不会使答案变差，故只需讨论 $x_m \le u$ 的情况，同理，也只需讨论 $x_{m + 1} \ge v$ 的情况，因此只需考虑 $x_m \le u$ 且 $x_{m + 1} \ge v$ 的情况

引理

下面证明一个引理：

若对于 $a_{1 \sim n}$ 的最优解为 $\{b_i\} = k$ ，则对于任意一组解（不一定最优） $\{b_i\} = \{x_i\}$ 满足 $x_1 > k$ （因为单调性，其实就是 $\forall i \in [1, n], x_i > k$ ），将其改为 $\{b_i\} = t(k \le t \le x_1)$ 一定不会比 $\{b_i\} = \{x_i\}$ 差

引理1

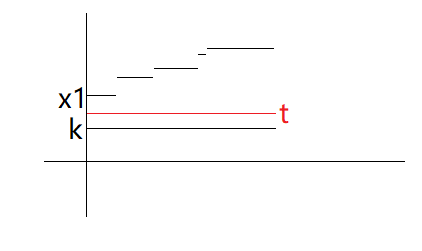
如图，将解 $\{b_i\} = \{x_i\}$ 替换成 $\{b_i\} = t$ 答案不会变差

先证明：将解变为 $\{b_i\} = x_1$ 答案不会变差

考虑将第二段及以后的 $x$ 整体下移 $\Delta$ 个单位使得第二段平移到于第一段水平的位置，如图：

平移

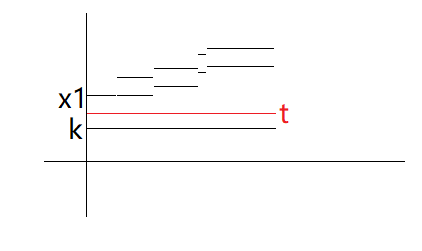
考虑被平移部分的 $a$ 的中位数，设其为 $k’$ ，若 $k’ > k$ 那么对于被平移部分，取 $k’$ 显然比取 $k$ 更优，则与 $k$ 的“最优”性质矛盾，所以必有 $k’ \le k$ （此时因为单调性不能让 $k$ 等于 $k’$ ），因此被平移部分至少有一半的 $a$ 是小于等于 $k$ 的，我们将对应的 $x$ 下移，会使这些所有数的答案分别变优 $\Delta$ ，而另外 $a$ 大于 $k$ 的部分答案会变差 $\Delta$ 但变优的比变差的多，所以总的答案不会变差；以此类推，将每一段都下移，解不会变差

然后我们来看原命题，就变得很简单了，由 $k$ 的最优性， $\{b_i\} = k$ 一定比 $\{b_i\} = x_1$ 优，而 $x_1$ 越靠近 $k$ 就越优（准确的说是不会变差），所以取在 $x_1, k$ 间的任意值 $t$ 替代 $x_1$ 答案不会变差

需要注意的是，当 $k$ 比 $\{x_i\}$ 都大时，结论任成立，即上图的情况反过来也行

正确性2

回到刚从证明正确性

刚才已经说过，只需考虑 $x_m \le u$ 且 $x_{m + 1} \ge v$ 的情况，即如图：

2

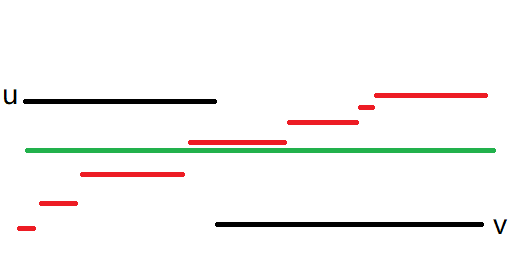
$u, v$ 以 $m$ 为界，分别时前一半的最优解和后一半的最优解，红色部分是一组整体的最优解，由刚才的引理，红色部分可以替换为绿色部分，解不会变差，也就是说：存在一组全段都相等的最优解，明显，此时应该是整段的中位数

于是转化的做法的正确性成立

实现

下面考虑如何用左偏树实现该过程

类似动态维护中位数的思想，我们用左偏树维护较小一半数，其最大值就是中位数

设当前段中位数为 $u$ ，新段中位数为 $v$ ，合并完后中位数为 $w$

每次需要合并的情况一定是新段的中位数小于当前中位数，即 $v < u$ 时，则易证合并完毕后新的中位数一定在原来两个中位数之间，即 $v \le w \le u$ ，此时如果新的中位数是新段中的某个数，由于新段的左偏树只维护了小于 $v$ 的数，所以我们就找不到 $w$ 了，换句话说，在没有限制的情况下，直接用左偏树维护中位数是不行的

但是，这道题还有一个特殊性质：每次新加的一段只有一个数（当然这个数就是中位数），换句话说，如果 $w$ 是在新加入的一段中，那么 $w$ 只可能等于 $v$ ，应为新段没有别的数了

但是又有一个问题：如果在某次插入完后，中位数变小了，导致不满足单调性（换句话说，变得比前一段小了），我们必须合并这个刚完成插入的段和前一段，此时这个段不是只有一个数啊

同上设原中位数为 $u$ ，新中位数为 $w$ ，而这一段的前一段中位数为 $k$ ，显然有 $w < k < u$

我们考虑到，这一段插入了一个新的点，中位数只会变化一个位置，换句话说，在这一段上 $w$ 和 $u$ 之间是没有数的（ $k$ 在前一段上），而 $k < u$ ，故在这一段上， $w, k$ 之间也是没有数的，所以这一段和前一段合并后的中位数要么是 $w$ ，要么在前一段上，不会出现在这一段上且大于 $w$ 的情况

于是可以用左偏树维护较小一半数来合并（注意维护较大的一半是不行的，因为合并后中位数会变小）

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int N = 1e6 + 5;
int n;
struct LeftHeap
{
	int l, r, v, dis;
#define l(x) lh[(x)].l
#define r(x) lh[(x)].r
#define v(x) lh[(x)].v
#define dis(x) lh[(x)].dis
} lh[N];
struct Line
{
	//终点,根,大小
	int ed, rt, si;
} stk[N];
int ans[N];
int merge(int x, int y)
{
	if (!x || !y)
		return x + y;
	if (v(x) < v(y))
		swap(x, y);
	r(x) = merge(r(x), y);
	if (dis(r(x)) > dis(l(x)))
		swap(r(x), l(x));
	dis(x) = dis(r(x)) + 1;
	return x;
}
int main()
{
	scanf("%d", &n);
	for (int i = 1; i <= n; ++i)
	{
		scanf("%d", &v(i));
		v(i) -= i; //转化为非严格
	}
	int top = 0;
	Line t;
	for (int i = 1; i <= n; ++i)
	{
		t = (Line){i, i, 1}; //只有一个的当前点
		dis(i) = 1; //当前点构成一棵左偏树
		while (top && v(t.rt) < v(stk[top].rt)) //小于的情况
		{
			t.rt = merge(t.rt, stk[top].rt);
			if (t.si & stk[top].si & 1) //如果两个区间都是奇数,合并后要弹出一个数
				t.rt = merge(l(t.rt), r(t.rt));
			t.si += stk[top].si;
			--top;
		}
		stk[++top] = t;
	}
	for (int i = 1, j = 0; i <= top; ++i)
		while (j < stk[i].ed)
			ans[++j] = v(stk[i].rt);
	LL as = 0;
	for (int i = 1; i <= n; i++)
		as += abs(v(i) - ans[i]);
	printf("%lld\n", as);
	for (int i = 1; i <= n; i++)
		printf("%d ", ans[i] + i);
	return 0;
}