Dyd's Blog

He who has a strong enough why can bear almost any how.

Dancing Links

Posted on Edited on In
Symbols count in article: 7.5k Reading time ≈ 7 mins.

跳舞表、舞蹈链（神一般的翻译）

Dancing Links

问题

Dancing Links（DLX）一般被用来解决一类“精确覆盖问题”：

给定一个 $n * m$ 的01矩阵，求最少要选出多少行，使得每一列恰好有一个1，如图，最少选两行（红色）：

精确覆盖

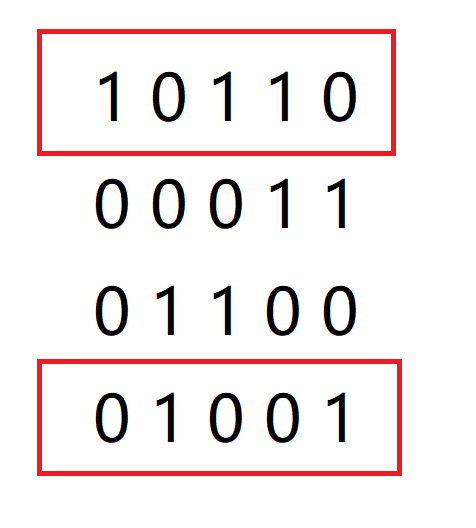
这是一个NPC问题，也就意味着我们只能暴力，但如何更聪明的暴力呢？

X算法

解决以上问题的暴力算法中，比较优秀的是二进制压缩和X算法，这里主要介绍X算法：

看到如下01矩阵：

1

我们先找到还未满足的、且包含1最少的一列（有多个就随便取一个），这样可以减少枚举（这个贪心的正确性显然），如图中红色的5列都满足条件，不妨取第一列

然后我们取第一列的两个1中任意一个所在行（蓝色），由于要求恰好有一个1，所以橘色行一定不可取，而绿色的列已经被满足了

2

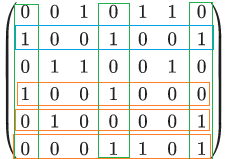
显然被标记（蓝、橘、绿）部分已经没有意义了，我们删去它们，得到更小的矩阵

4

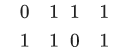
然后再选，这次假设我们选了现在的第一行，第二行也会被删掉，得到一个空矩阵，而得到空矩阵的这一步操作所删去的行并非全部为1，所以这不是一种合法的方案（如选则现在的第一行，现在的第一列就没有1，不符合要求）

怎么办？回溯啊，将我们删除的行、列加回来，再尝试另外一种删法

以上就是X算法，它看起来十分暴力，但可优化性极好，因为它含有很多的“加行、列，删行、列”操作，这提示我们用链表优化

DLX

DLX的使用必须满足一个条件：图是稀疏的，换句话说，图中的1的个数不多（但“不多”的定义到底是多少呢，我也不知道）

DLX是用了一个十字链表结构来优化的，具体的，一个为1点将与其上、下、左、右四个方向上的第一个1链接（如果走到边界就循环），如图：

十字链

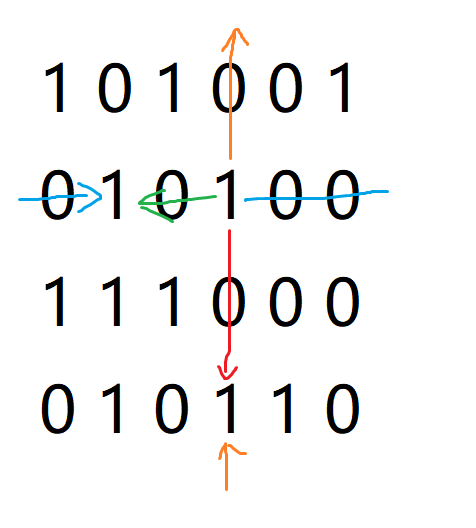
明显，这个链表是双向的

同时我们还需要记录下每一个1的行号、列号，以及每一列有多少个1（方便求1最少的一列）

我们要先建出一个空行来做表头，然后类似于链式前向星的插入，注意我们是每插入完一行就要换行

然后进行dfs搜索即可（dance操作）

代码和时间分析

精确覆盖问题

由于l、r、u等变量名很容易重名，所以用了个结构体

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
#include <bits/stdc++.h>
using namespace std;
const int N = 5500 + 5; //要多开m个表头
struct DLX
{
	int l[N], r[N], u[N], d[N]; //左、右、上、下
	int si[N], row[N], col[N]; //row:行号,col:列号
	int idx;
	vector<int> ans;
	void init(int x) //建出表头
	{
		ans.clear();
		for (int i = 0; i <= x; ++i)
		{
			l[i] = i - 1, r[i] = i + 1;
			col[i] = u[i] = d[i] = i;
    		si[i] = 0;
		}
		l[0] = x, r[x] = 0; //循环
		idx = x + 1;
	}
	void insert(int &hh, int &tt, int x, int y) //在hh和tt间插入点(x, y)
	{
		row[idx] = x, col[idx] = y, ++si[y];
		u[idx] = y, d[idx] = d[y], u[d[y]] = idx, d[y] = idx; //这里y是表头
		r[hh] = l[tt] = idx, r[idx] = tt, l[idx] = hh;
		tt = idx++;
	}
	void remove(int p) //删掉p所在列和该列有1的行
	{
		r[l[p]] = r[p], l[r[p]] = l[p];
		for (int i = d[p]; i != p; i = d[i])
			for (int j = r[i]; j != i; j = r[j])
			{
				--si[col[j]];
				u[d[j]] = u[j], d[u[j]] = d[j];
			}
	}
	void resume(int p) //添加p所在列和该列有1的行,注意和删除倒着来
	{
		for (int i = u[p]; i != p; i = u[i])
			for (int j = l[i]; j != i; j = l[j])
			{
				u[d[j]] = j, d[u[j]] = j;
				++si[col[j]];
			}
		r[l[p]] = p, l[r[p]] = p;
	}
	bool dance()
	{
		if (!r[0])
			return true;
		int p = r[0];
		for (int i = r[0]; i; i = r[i])
			if (si[i] < si[p])
				p = i;
		remove(p);
		for (int i = d[p]; i != p; i = d[i]) //尝试选p列中每一个有1的行
		{
			ans.push_back(row[i]);
			for (int j = r[i]; j != i; j = r[j])
				remove(col[j]);
			if (dance())
				return true;
			//回溯,注意反着来
			for (int j = l[i]; j != i; j = l[j])
				resume(col[j]);
			ans.pop_back();
		}
		resume(p);
		return false;
	}
} dlx;
int main()
{
	int n, m;
	scanf("%d%d", &n, &m);
	dlx.init(m);
	for (int i = 1, hh, tt, x; i <= n; ++i)
	{
		hh = tt = dlx.idx; //换行
		for (int j = 1; j <= m; ++j)
		{
			scanf("%d", &x);
			if (x)
				dlx.insert(hh, tt, i, j);
		}
	}
	if (dlx.dance())
	{
		for (int i : dlx.ans)
			printf("%d ", i);
		puts("");
	}
	else
		puts("No Solution!");
	return 0;
}

DLX递归及回溯的次数只与矩阵中1的个数有关，它的实际复杂度为 $O(c^n)$ ，其中 $c$ 是一个很接近于1的常数，而 $n$ 是矩阵中1的个数

与Dinic、匈牙利类似，DLX的实际运行情况良好

应用——数独

DLX有很多应用，最经典的是数独问题，DLX 的难点，不全在于链表的建立，而在于建模，即如何转化为精确覆盖问题，一般来说，我们会赋予行列意义，行表示决策，对应选或不选，列表示限制，对应题目条件

那么看看数独问题：数独

每一次填数可以用一个三元组 $(x, y, z)$ 表示，意为“在第 $x$ 行第 $y$ 列填入数字 $z$ ”，而题目的限制有四个：每个格子只能填一个数，行、列、九宫格要满足不重复

那么考虑如何定义DLX的行和列：

行对应决策，很好定义，因为三元组 $(x, y, z)$ 中 $x, y, z \in [1, 9]$ 故一共有 $9^3 = 729$ 种决策，我们就让DLX中有729行

而列对应限制，先考虑每个格子只能填一个数，我们需要81列来保证这个性质；然后，对于数独中的每一行，我们需要一列保证该行有且仅有一个1，又一列保证该行有且仅有一个2，……，最终对于数独中的每一行，我们要9列，一共9行，则为了保证数独的行不重复，我们要 $9 \times 9 = 81$ 行；对于数独的列、九宫同理，一共要用 $81 \times 4 = 324$ 列

而DLX的729行中每一行对应一个决策，即填入一个数字，这只会影响四个限制各一个，故有 $729 \times 4 = 2916$ 个1

综上，我们的DLX有729行，324列，2916个1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
#include <bits/stdc++.h>
using namespace std;
const int N = 5000 + 5;
int a[10][10];
struct DLX
{
	int l[N], r[N], u[N], d[N];
	int si[N], row[N], col[N];
	int idx;
	vector<int> ans;
	void init(int x)
	{
		ans.clear();
		for (int i = 0; i <= x; ++i)
		{
			l[i] = i - 1, r[i] = i + 1;
			col[i] = u[i] = d[i] = i;
    		si[i] = 0;
		}
		l[0] = x, r[x] = 0;
		idx = x + 1;
	}
	void insert(int &hh, int &tt, int x, int y)
	{
		row[idx] = x, col[idx] = y, ++si[y];
		u[idx] = y, d[idx] = d[y], u[d[y]] = idx, d[y] = idx;
		r[hh] = l[tt] = idx, r[idx] = tt, l[idx] = hh;
		tt = idx++;
	}
	void remove(int p)
	{
		r[l[p]] = r[p], l[r[p]] = l[p];
		for (int i = d[p]; i != p; i = d[i])
			for (int j = r[i]; j != i; j = r[j])
			{
				--si[col[j]];
				u[d[j]] = u[j], d[u[j]] = d[j];
			}
	}
	void resume(int p)
	{
		for (int i = u[p]; i != p; i = u[i])
			for (int j = l[i]; j != i; j = l[j])
			{
				u[d[j]] = j, d[u[j]] = j;
				++si[col[j]];
			}
		r[l[p]] = p, l[r[p]] = p;
	}
	bool dance()
	{
		if (!r[0])
			return true;
		int p = r[0];
		for (int i = r[0]; i; i = r[i])
			if (si[i] < si[p])
				p = i;
		remove(p);
		for (int i = d[p]; i != p; i = d[i])
		{
			ans.push_back(row[i]);
			for (int j = r[i]; j != i; j = r[j])
				remove(col[j]);
			if (dance())
				return true;
			for (int j = l[i]; j != i; j = l[j])
				resume(col[j]);
			ans.pop_back();
		}
		resume(p);
		return false;
	}
} dlx;
int get_id(int x, int y, int num)
{
	return (x - 1) * 9 * 9 + (y - 1) * 9 + num;
}
void insert(int x, int y, int num)
{
	int dx = (x - 1) / 3 + 1;
	int dy = (y - 1) / 3 + 1;
	int room = (dx - 1) * 3 + dy, id = get_id(x, y, num);
	int hh = dlx.idx, tt = dlx.idx;
	dlx.insert(hh, tt, id, 81 * 0 + (x - 1) * 9 + y);
	dlx.insert(hh, tt, id, 81 * 1 + (x - 1) * 9 + num);
	dlx.insert(hh, tt, id, 81 * 2 + (y - 1) * 9 + num);
	dlx.insert(hh, tt, id, 81 * 3 + (room - 1) * 9 + num);
}
void get_ans()
{
	int x, y, z;
	for (int i : dlx.ans)
	{
		x = (i - 1) / 9 / 9 + 1;
		y = (i - 1) / 9 % 9 + 1;
		z = (i - 1) % 9 + 1;
		a[x][y] = z;
	}
}
int main()
{
	dlx.init(324);
	for (int i = 1; i <= 9; ++i)
		for (int j = 1; j <= 9; ++j)
		{
			scanf("%d", &a[i][j]);
			if (a[i][j])
				insert(i, j, a[i][j]);
			else
				for (int k = 1; k <= 9; ++k)
					insert(i, j, k);
		}
	dlx.dance();
	get_ans();
	for (int i = 1; i <= 9; ++i)
	{
		for (int j = 1; j <= 9; ++j)
			printf("%d ", a[i][j]);
		putchar('\n');
	}
	return 0;
}

拓展应用——重复覆盖问题

在精确覆盖问题中，考虑将条件“每一列恰好有一个1”改为“每一列至少有一个1”，这个问题就是重复覆盖问题

解决重复覆盖问题和精确覆盖问题一样，主要还是DLX，即十字双向链表优化dfs，不同的地方是，每次删除的时候只删掉所选行的所有1所在列，并不像精确覆盖一样删掉和1同列的所有1的所在行（这是因为可以重复覆盖），这样，dfs的深度将变得无法预测，于是我们使用IDA*

此时就不需要保证矩阵中1的个数不多了，反而，我们需要保证答案选的行数不多，另外重复覆盖问题很暴力，所以容易TLE

重复覆盖问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
#include <bits/stdc++.h>
using namespace std;
const int N = 10000 + 5, NN = 100 + 5;
int n, m;
struct DLX
{
	int l[N], r[N], u[N], d[N];
	int si[N], row[N], col[N];
	int idx;
	bool vis[NN];
	vector<int> ans;
	void init(int x)
	{
		ans.clear();
		for (int i = 0; i <= x; ++i)
		{
			l[i] = i - 1, r[i] = i + 1;
			col[i] = u[i] = d[i] = i;
			si[i] = 0;
		}
		l[0] = x, r[x] = 0;
		idx = x + 1;
	}
	void insert(int &hh, int &tt, int x, int y)
	{
		row[idx] = x, col[idx] = y, ++si[y];
		u[idx] = y, d[idx] = d[y], u[d[y]] = idx, d[y] = idx;
		r[hh] = l[tt] = idx, r[idx] = tt, l[idx] = hh;
		tt = idx++;
	}
	void remove(int p) //删除p列
	{
		for (int i = d[p]; i != p; i = d[i])
		{
			r[l[i]] = r[i];
			l[r[i]] = l[i];
		}
	}
	void resume(int p)
	{
		for (int i = u[p]; i != p; i = u[i])
		{
			r[l[i]] = i;
			l[r[i]] = i;
		}
	}
	int h()
	{
		int res = 0;
		for (int i = 1; i <= n; ++i)
			vis[i] = false;
		for (int i = r[0]; i; i = r[i])
		{
			if (vis[col[i]])
				continue;
			++res;
			vis[col[i]] = true;
			for (int j = d[i]; j != i; j = d[j])
				for (int k = r[j]; k != j; k = r[k])
					vis[col[k]] = true;
		}
		return res;
	}
	bool dance(int o, int depth)
	{
		if (o + h() > depth)
			return false;
		if (!r[0])
			return true;
		int p = r[0];
		for (int i = r[0]; i; i = r[i])
			if (si[i] < si[p])
				p = i;
		for (int i = d[p]; i != p; i = d[i])
		{
			ans.push_back(row[i]);
			remove(i);
			for (int j = r[i]; j != i; j = r[j])
				remove(j);
			if (dance(o + 1, depth))
				return true;
			for (int j = l[i]; j != i; j = l[j])
				resume(j);
			resume(i);
			ans.pop_back();
		}
		return false;
	}
} dlx;
int main()
{
	
	scanf("%d%d", &n, &m);
	dlx.init(m);
	for (int i = 1, hh, tt, x; i <= n; ++i)
	{
		hh = tt = dlx.idx; //换行
		for (int j = 1; j <= m; ++j)
		{
			scanf("%d", &x);
			if (x)
				dlx.insert(hh, tt, i, j);
		}
	}
	int depth = 0;
	while (!dlx.dance(0, depth))
		++depth;
	printf("%d\n", depth);
	for (int i : dlx.ans)
		printf("%d ", i);
	return 0;
}