马拉车算法

Manacher

思路

Manacher算法是一中可以在 $O(n)$ 时间内求出最长回文子串的算法（以前的 $O(n \log n)$ hash+二分可以退役了）

在使用马拉车前，由于马拉车只能求长度为奇数的回文串，所有我们首先要有一个转换，把长度为偶数的回文串化为长度为奇数，具体方法为：

在字符串的头部插入开始符（一般为“\$”），在尾部插入结尾符（一般为“^”），然后每两个字符间都插入一个分隔符（一般为“#”），例如，字符串“abbcac”转化后就是“\$#a#b#b#c#a#c#^”，这样，就可以把原串的每一个回文串都化为一个“由#开头和结尾的长度为奇数的回文串”

然后，考虑如何求最大的长度为奇数的回文串

类似kmp我们扫描整个串，记 $p[i]$ 表示“以 $i$ 为中点的最长回文串的长度的一半（包括 $i$ ）”，考虑用已有的信息求出现在的 $p[i]$

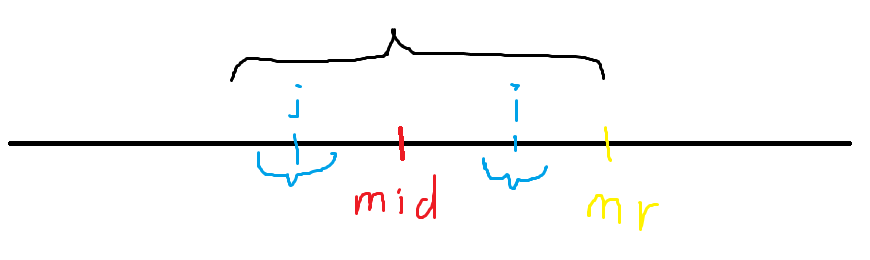
如图，假设现在要求 $p[i]$ ，则 $p[1 \sim i - 1]$ 已知，定义一个回文串的位置为 $[l, r]$ ，则已知的最大的 $r$ 记为 $mr(maxright)$ ，其对应的回文串中点为 $mid$ ，则分类讨论：

• $i > mr$ ，此时先令 $p[i] = 1$

• $i \le mr$ 此时必有 $j = mid * 2 - i$ 与 $i$ 对应，再次分类：

  1. $p[j] \le mr - i + 1$ ，此时 $j$ 所在的最大回文串全部能和 $i$ 对应（图中蓝色部分），让 $p[i] = p[j]$
  2. $p[j] > mr - i + 1$ ，此时由于 $mr$ 右边的情况未知，故只能先让 $p[i] = mr - i + 1$

由上，我们通过已有的信息计算出了“保证合法但不保证最大的情况下 $p[i]$ 的值”，其中没有保证最大的原因是 $mr$ 右边的情况不知道，若 $i$ 所在的最大回文串的右边界大于 $mr$ ，就无法统计，解决办法是——暴力！对于分类讨论得到的 $p[i]$ ，我们暴力尝试让它加1，直到不行为止

最后统计答案时，由于 $p[i]$ 只是长度的一半应该要乘二，但由于我们把原串扩充了一倍，所以实际答案就是 $\max_{i = 1}^{n}(p[i] - 1)$

需要注意的是，在具体的代码实现中，常常让 $mr = mr + 1$ ，换句话说，以 $mid$ 为中心的最大回文串不是 $[l, r]$ ，而是 $[l, r)$ ，上面讲成闭区间只是为了方便理解

代码

【模板】manacher 算法

#include <bits/stdc++.h>
using namespace std;
const int N = 1.1e7 + 5;
int n;
char a[N], b[N << 1];  //二倍
int p[N << 1];
void init()
{
	int k = 0;
	b[++k] = '$', b[++k] = '#';
	for (int i = 1; i <= n; ++i)
		b[++k] = a[i], b[++k] = '#';
	b[++k] = '^';
	n = k;
}
void manacher()
{
	int mr = 0, mid;
	for (int i = 2; i <= n; ++i)
	{
		if (i < mr)
			p[i] = min(p[mid * 2 - i], mr - i);
		else
			p[i] = 1;
		while (b[i - p[i]] == b[i + p[i]])
			++p[i];
		if (i + p[i] > mr)
			mr = i + p[i], mid = i;
	}
}
int main()
{
	scanf("%s", a + 1);
	int ans = 0;
	n = strlen(a + 1);
	init();
	manacher();
	for (int i = 1; i <= n; ++i)
		ans = max(ans, p[i]);
	printf("%d\n", ans - 1);
	return 0;
}

时间复杂度

和kmp一样，马拉车的两个循环也是“假的”，简证：

首先，如果 $i$ 所在的最大回文串 $[l, r]$ 的右断点 $r \le mr$ ，while只会执行一次，因为如果此时 $p[i]$ 一定是与 $p[j]$ 对于的，若还可以加1，这与 $p[j]$ 的“最大”矛盾

其次，若 $r > mr$ ，则一定会跟新 $mr$ ，而 $mr$ 明显是不下降的，当 $mr = n$ 时，就不可能再有 $r > mr$ 了，换句话说， $mr$ 最多遍历一次 $n$ ，之后就不会再跟新 $mr$ 也就不会再有 $r > mr$ 了

综上，马拉车的时间复杂度为 $O(n)$