我以为很好打……
一道很难的题,但可以骗点分
首先第一眼看过去就是dp, $n, m \le 50$ 说明dp并不简单,但看数据范围,反正我是想打分段骗分
数据1
$n, m \le 4$ 直接dfs,注意题目求的是扫地机器人在撞上障碍之前,经过了多少个格子,换句话说,没撞上障碍,贡献是0
20分到手
数据2
打表
除了起点外所有格子都是障碍,明显答案就是所有的方案都输入到了扫地机器人里,但 $n, m \le 50$ ,暴力求所有的方案数时间复杂度和数据1是一样的,但是,通过上面的暴力程序打个小表(把dfs能跑出来的全打了)来找规律,发现对于 $n, m$ (不妨设 $n \le m$ ),若 $n \mid m$ ,有如下表:
| n | m | Ans |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 2 | 1 |
| 1 | 3 | 1 |
| 2 | 2 | 2 |
| 2 | 4 | 2 |
| 2 | 6 | 2 |
| 3 | 3 | 6 |
| 3 | 6 | 3 |
| 3 | 9 | 6 |
| 3 | 12 | 3 |
| 4 | 4 | 8 |
| 4 | 8 | 8 |
| 4 | 12 | 4 |
而若 $n \not\mid m$ ,答案为0,找一手规律,信心满满交上去,WA了
好吧,看来没有想象的简单,我们发现我们枚举的数都太小了,它们的合数只有4,而且4还没枚举完,但这已经提示我们和gcd或者互质有关系
性质1
再认真看看打出来的表,以及对应的合法方案数
发现一个性质:对于一个点 $(x, y)$ ,若它走向 $(x + 1, y)$ ,则 $(x, y + 1)$ ,一定是由 $(x - 1, y + 1)$ 走来;同样的,若它走向 $(x, y + 1)$ ,则 $(x + 1, y)$ ,一定是由 $(x + 1, y - 1)$ 走来,正确性显然
参考下图:
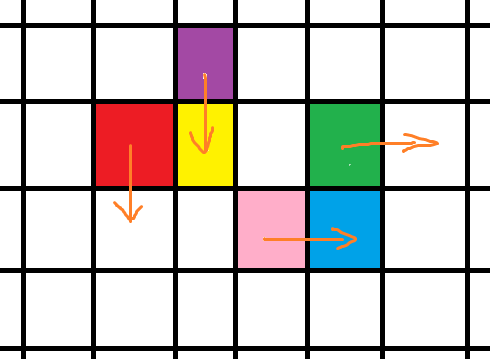
若红点向下,则黄点一定是由紫色向下走到(因为红点已经不可能再向右了),绿、蓝、粉点同理,换句话说,红、紫(绿、粉)点的方向一定相同
再参考样例:
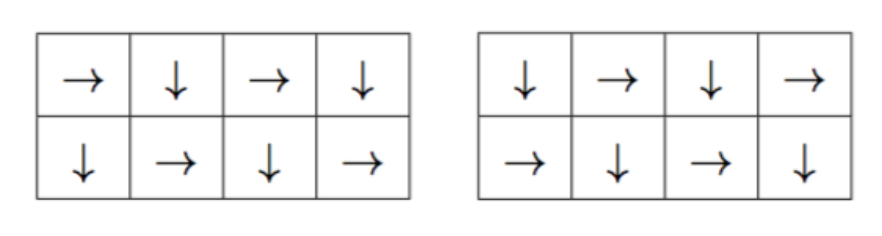
推广到整个图:一个矩形内任意一条从右上到左下的对角线方向相同,其中“一条从右上到左下的对角线”是包含了循环的,如图,颜色相同的是“一条对角线”
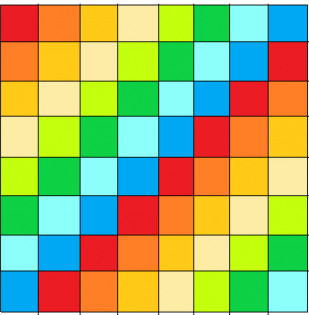
这也和我们上面打的表相符合
性质2
由于一个点左下和右下的元素属于同一对角线,所以我们下一步无论怎么走都会走到同一个对角线上,则下一步的方向已经确定,推广一下:机器人的动作自然就是循环的
循环节很好求,就是看走多少部可以回到原对角线,手玩一下发现是 $gcd(n, m)$ ,这也和打表的猜测相符合
证明的话(听大佬说是)把这个矩阵复制几份拼在一起,如果循环节不是 $gcd(n, m)$ 那么在两个矩形的交界出会出现副对角线颜色不同的情况,而循环节是 $gcd(n, m)$ 的时候相当于一堆正方形拼在一起自然不会出现问题
性质3
设循环节长度为 $d$ ,且其中有 $a$ 步向右, $d - a$ 步向下,则有 $a \perp d$ 且 $a \perp n, (d - a) \perp m$
证明:
若可到节点 $(x, y)$,则有 $1 + ka \equiv x \pmod n$ ,而 $x$ 取遍 $1 \sim n$ ,由裴蜀定理,若 $gcd(a, n) \ne 1$ ,则必有 $x$ 取不到,故 $a \perp n$
同理有 $gcd(d - a, m) = 1$ ,又因为 $d = gcd(n, m)$ ,故 $a \perp d$
结论
有了以上性质,方案数变得可求,考虑枚举 $a$ 即可
$$
Ans = \sum_{a = 0} ^ {d} [a \perp d] * [a \perp n] * [(d - a) \perp m] * \binom{d}{a}
$$
期望得分50
数据3
现在考虑撞上障碍,明显应该dp,由于 $n, m$ 很小,dp状态几乎可以随便设,反正维数管够,设 $f[i][j][k]$ 表示在 $(i, j)$ 上撞上障碍的路程的最小值为k的方案数
同数据2,可以枚举 $a$ ,易得,若该次循环从 $(x, y)$ 出发,必然走到 $(x + a, y + b)$ ,所以只要在 $(1, 1)$ 到 $(1 + a, 1 + b)$ 间dp即可
设格子 $(x, y), (1 \le x \le 1 + a, 1 \le y \le 1 + b)$ 的权值 $w_{x, y}$ 为走到有障碍格子 $(x + ka, y + kb), (k \in \mathbb{N})$ 的最小步数,则方程为
$$
\begin{align}
f[i][j][k] \rightarrow f[i + 1][j][\min (k, w_{i + 1, j})]\\
f[i][j][k] \rightarrow f[i][j + 1][\min (k, w_{i, j + 1})]
\end{align}
$$
考虑时间复杂度,求 $w[i][j]$ 需要枚举 $a, i, j, k$ ,$a, i, j \le d$ ,而 $k \le \frac{nm}{d}$ ,总的时间复杂度为 $O(d^2nm) < O(n^4)$ ,而转移 $f$ 时要枚举 $i, j, k$ ,其中 $i \le n, j \le m, k \le nm$ 故为 $O(n^4)$ ,总的时间复杂度为 $O(Tn^4)$ ,大概 $6 \times 10^8$ 的样子,由于有很多条件特判(如 $a$ 的互质),跑不满(实测跑的飞快),加上时限是5s,可以过
1 |
|