一定要理解它与“域”的广义关系

线性基

线性基是竞赛中常用来解决子集异或一类题目的算法

数学相关定义

一大堆没用的

向量空间

向量空间亦称线性空间，具体可见百度百科，反正简单来说，就是定义了加法和乘法和对应单位元的向量的集合（其实完全不一样，但我们只需要用到这么多）

线性相关和线性无关

若 $V$ 是一个向量空间（集合），如果存在不全为零的系数数列 $c_1, c_2, …, c_n \in \mathbb{F}$ （ $\mathbb{F}$ 是代数域），使得 $c_1 \vec{v_1} + c_2 \vec{v_2} + … +c_n \vec{v_n} = 0$ （即 $\exists \vec{v_j}$ 可以被除它本身外其它属于 $V$ 的向量表示出来），那么 $V$ 中的向量就叫做线性相关的，反之，则为线性无关的

子空间

设 $W$ 为向量空间 $V$ 的一个非空子集，若 $W$ 在 $V$ 的加法及标量乘法下是封闭的，且零向量 $\vec{0} \in W$ ，就称 $W$ 为 $V$ 的线性子空间，简称子空间

扩张和生成集合

给出一个向量集合 $B$ ，那么包含它的最小子空间 $W$ 就称为它的扩张（也叫张成），记作 $span(B)$ ，另外规定空集的扩张为 ${\vec{0}}$

而 $B$ 也被叫做 $W$ 的生成集合（可以理解为通过 $B$ 中的元素可以将 $W$ 中的所有元素表示出来）

基和维度

给出一个向量集合 $B$ ，若 $B$ 是线性无关的，且 $B$ 能够生成 $V$ ，就称 $B$ 为 $V$ 的一个基

对非零向量空间 $V$ ，基是 $V$ 最小的生成集，也是极大线性无关组

如果一个向量空间 $V$ 拥有一个元素个数有限的生成集，那么就称 $V$ 是一个有限维空间，向量空间的所有基拥有相同基数，称为该空间的维度

空间内的每个向量都有唯一的方法表达成基中向量的线性组合，而且，将基中向量进行排列，表示成有序基，每个向量便可以坐标系统来表示，有点像“平面向量基本定理”

线性基

扯了那么多没有用的，下面才是真的要用的

考虑 $m$ 个 $n$ 维向量（ $m > n$ ），可以写成矩阵：
$$
\begin{aligned}
\begin{bmatrix}
\vec{v_1} \\
\vec{v_2} \\
… \\
\vec{v_m} \\
\end{bmatrix}
=
\begin{bmatrix}
a_{1, 1} \ a_{1,2} \ … \ a_{1, n} \\
a_{2, 1} \ a_{2,2} \ … \ a_{2, n} \\
… \\
a_{m, 1} \ a_{m,2} \ … \ a_{m, n} \\
\end{bmatrix}
\end{aligned}
$$
由高斯消元可知， $n$ 个变量最少只要需要 $n$ 个方程就可以唯一确定，则 $m$ 行中可能有一些行消元后全为 $0$ ，对应到向量就是可被表示（这也说明 $n$ 维向量的基长度最大为 $n$ ）

顺便一提，而消完元后剩下的非 $0$ 行/列就叫矩阵的行/列秩（ rank ），对应到向量中就是基（即极大线性无关组）的大小

定义

线性基其实就是上面数学定义中，将向量空间的加法和乘法定义为异或的意义下的基，我们考虑对于一个 $n$ 位 $2$ 进制数，可以看作一个 $n$ 维向量，异或看作对 $2$ 取模意义下的加法，它的乘法就定义为只能乘 $0, 1$ （因为只有 $0, 1$ ，消元时也就只需要乘 $0, 1$ ），更形式化的，在异或的定义下：

• 用无符号整数集来替代向量的集合
• 对于集合 $B$ ，在其中选出任意多个数，其异或和的所有可能的结果组成的集合 $S$ 称作 $B$ 的扩张，记为 $span(B)$
• 对于一个集合 $B$ ，若存在一个元素可以用其它若干个元素异或起来得到，则称 $B$ 中元素线性相关，反之，则为线性无关
• 对于集合 $B, S$ ，若 $S \subseteq span(B)$ 且 $B$ 线性无关，则称 $B$ 为 $S$ 的线性基，集合 $B$ 中元素的个数，称为线性基的长度

个人觉得对照这数学中的定义还是比较好理解的

性质

若 $B$ 是 $S$ 的线性基，则 $S$ 中的任意元素都可以唯一表示为 $B$ 中若干个元素异或起来的结果，正确性显然

构造

设向量为 $L$ 维，如果直接高斯， $O(L^3)$ 爆炸，考虑异或的特殊性质，设线性基中向量为 $\vec{v_1}, \vec{v_2}, … \vec{v_L}$ ，我们规定只有 $\vec{v_i}$ 的第 $i$ 维为 $1$ ，那么在插入一个数时，我们采用逆序枚举 $t$ 所以为1的二进制位 $j$ ，对于每个 $j$ ：

1. 若 $a[j] \ne 0$ ，则 $t = t \oplus a[j]$
2. 若 $a[j] = 0$ ，则 $a[i] = t$ ，结束

若用 bitset 实现，构造线性基的时间为 $O(\frac{n L^2}{w})$ （单次插入 $O(\frac{L^2}{w})$ ），对于一般的 int ， long long 数据就是 $O(nL)$ （单次插入 $O(L)$ ），此时最好用数组实现

用途

线性基支持以下操作：

• 求集合的最大异或和：

  只需倒序枚举每一个 $a[i]$ ，贪心异或即可

• 求集合的最小异或和：

  先特判能否为 0 ，然后正序序枚举每一个 $a[i]$ ，第一个存在的就是答案

• 查询 $t$ 是否在值域中

  类似于插入

• 查询第 $k$ 小的值

  先特判减去0，然后从高到低处理线性基每一位，对于每一位向后扫，如果当前数第 $i$ 位为0，且线性基第 $i$ 位不为0，则将当前数异或上 $a[i]$ ，这一操作可以在 $O(L^2)$ 的时间内解决，我们称其为重构
  经过这一步操作后，设线性基内共有 $si$ 个数，则它们共可以表示出 $2^{si}$ 个数
  随后，我们考虑将 $k$ 二进制拆分，用与快速幂类似的方法就可以求出第 $k$ 小值

代码

注意 long long ，这是数组实现

#include <bits/stdc++.h>
#define STC static
using LL = long long;
int n; //n是题目中插入到线性基里的个数
namespace LB  //Linear Basis
{
    const int L = 63;
    LL a[L + 5], si;
    void clear(){ memset(a, 0, sizeof a), si = 0; }
    void ins(LL  x)
    {
        for (int i = L; ~i; --i) if ((x >> i) & 1)
            if (!a[i]) return ++si, void(a[i] = x);
            else x ^= a[i];
    }
    LL gmx() //get max
    {
        LL res = 0;
        for (int i = L; ~i; --i) res = std::max(res ^ a[i], res);
        return res;
    }
    LL gmn() //get min
    {
        if (si < n) return 0;
        for (int i = 0; i <= L; ++i) if (a[i]) return a[i];
    }
    bool chk(LL x)
    {
        for (int i = L; ~i; --i) if ((x >> i) & 1)
            if (!a[i]) return false;
            else x ^= a[i];
        return true;
    }
    void reb() //rebuild
    {
        STC int tp[L + 5];
        si = 0;
        for (int i = 0; i <= L; ++i)
        {
            for (int j = i - 1; ~j; --j) if ((a[i] >> j) & 1) a[i] ^= a[j];
            if (a[i]) tp[si++] = a[i];
        }
        for (int i = 0; i < si; ++i) a[i] = tp[i];
    }
    LL gk(LL k) //get k
    {
        LL res = 0;
        if (si < n && !(--k)) return 0;
        if (k >= (1ll << si)) return -1;
        for (int i = 0; i < si; ++i) if ((k >> i) & 1) res ^= a[i];
        return res;
    }
}

例题

一般不会直接考板子，需要有些神仙转化

例题一

DZY Loves Chinese II

考虑到 dark bzoj 可能会挂，简述一下题意：给定 $n \le 10^5$ 个点 $m \le 5 \times 10^5$ 条边的无向图，有 $Q \le 5 \times 10^5$ 次询问，每次删除 $k \le 15$ 条边（询问之间独立），问图是否联通，强制在线

如果没有强制在线，直接离线以后分治乱搞，但强制在线了，我们考虑一个神仙转化：先随便取原图的一个最小生成树，然后给所以非树边随机赋一个权值；如果一个非树边连接 $u, v$ 权值为 $val$ ，就让树上连接 $u, v$ 的所有边的权值 $\oplus val$

以上步骤可以 dfs + 树上差分 $O(n)$ 解决，此时对于一条树上的边 $e$ ，删去了它后仍然能使图联通的所有边（或者说可以替代它的边）与它的异或和为 $0$ （因为它的权值就是可以替代它的边的权值异或和），由于是随机化的，我们认为只有这种可以互相替代的边构成的边集异或和为 $0$ ，其它边集异或和一定不为 $0$

那么问题变成给定 $k$ 个数求它是否有个子集异或和为 $0$ ，直接对这 $k$ 个数建线性基即可（注意到 $k$ 不大，这也使我们的随机化算法正确性更高了）

代码：

#include <bits/stdc++.h>
#define pb push_back
#define fi first
#define se second
#define FF std::function
using PII = std::pair<int, int>;
using uint = unsigned int;
using std::cerr;
const int N = 1e5 + 100, M = 5e5 + 100, K = 15 + 5;
int n, m, dep[N], q, k, c, last = 0;
uint val[M], sum[N];
std::vector<PII> G[N];
PII e[M];
bool vis[N], ist[M]; //ist:是否为树边
void mdf(int x, int y, uint d){ sum[y] ^= d, sum[x] ^= d; }
void get_val()
{
    std::mt19937 rud;
    for (int i = 1; i <= m; ++i) if (!ist[i]) mdf(e[i].fi, e[i].se, val[i] = rud());
    FF<void(int, int, int)> dfs = [&](int x, int fa, int in)
    {
        for (PII t : G[x]) if (ist[t.se] && t.fi != fa)
        {
            dfs(t.fi, x, t.se);
            sum[x] ^= sum[t.fi];
        }
        val[in] = sum[x];
    } ;
    dfs(1, 0, 0);
}
namespace LB //Linear Basis
{
    const int L = 31;
    uint a[L + 5], si;
    void clear(){ memset(a, 0, sizeof a), si = 0; }
    void ins(int  x)
    {
        for (int i = L; ~i; --i) if ((x >> i) & 1)
            if (!a[i]) return ++si, void(a[i] = x);
            else x ^= a[i];
    }
}
int main()
{
    scanf("%d %d", &n, &m);
    for (int i = 1; i <= m; ++i)
    {
        scanf("%d %d", &e[i].fi, &e[i].se);
        G[e[i].fi].pb({e[i].se, i}), G[e[i].se].pb({e[i].fi, i});
    }
    FF<void(int, int)> dfs = [&](int x, int fa)
    {
        vis[x] = true, dep[x] = dep[fa] + 1;
        for (PII t : G[x]) if (!vis[t.fi] && (ist[t.se] = true)) dfs(t.fi, x); 
    } ;
    dfs(1, 0), get_val();
    for (scanf("%d", &q); q--; )
    {
        scanf("%d", &k);
        LB::clear();
        for (int i = 1; i <= k; ++i) scanf("%d", &c), LB::ins(val[c ^ last]);
        if (k > LB::si) puts("Disconnected");
        else puts("Connected"), ++last;
    }
    return 0;
}

例题二

没找到 OJ 有题，口胡一下：

题面：

有 $n$ 个数,初始都是 $0$ ，有 $m$ 种操作,每个操作有 4 个参数 $l,r,v,c$ ，表示这个操作可以给 $[l,r]$ 内所有数异或上 $[1,v]$ 内的一个任意一个数,代价为 $c$ ，每个操作可以执行多次,一个操作序列的代价是使用过的操作代价最大值，每个操作序列会得到若干种终止状态，每种终止状态的贡献是能得到它的操作序列中代价的最小值,询问所有可能被得到的终止状态的贡献总和，答案对 $10^9+7$ 取模， $1\le n,m\le 10^5,1\le l\le r\le n, 1\le c\le 10^9,1\le v\le 2^{16\times 2^{16}}$ ， $v$ 会通过给定的随机数生成器来读入

思路：

发现这个 $v$ 范围非常阴间，所以，先假设 $v$ 在阳间范围内

这个“能得到它的操作序列中代价的最小值”不好搞，而且“代价恰为 $x$ 能得到的序列个数”也不好搞，考虑差分，记 $F(x)$ 为“代价小于等于 $x$ 能得到的序列个数”，则答案是 $Ans = \sum_{x} x (F(x) - F(x - 1))$ ，现在要求 $f(x)$ ，把操作按 $c$ 排序依次加入，考虑每一次加入后维护新的 $F(x)$ ，把每二进制下一位分开考虑，设 $f(i, x)$ 是“代价小于等于 $x$ 能得到的第 $i$ 位序列个数（这个序列显然是个 $01$ 序列）“，则 $F(x) = \prod_{i} f(i, x)$ ，那么对于每个 $i$ 考虑求 $f(i, x)$

考虑每次操作对第 $i$ 位的贡献，设 $k$ 是满足 $2^k \le v$ 的最大整数，那么当 $i \le k$ 时， $[l, r]$ 中的所有数第 $k$ 位就可以一起异或一个 $1$ ，画个矩阵出来：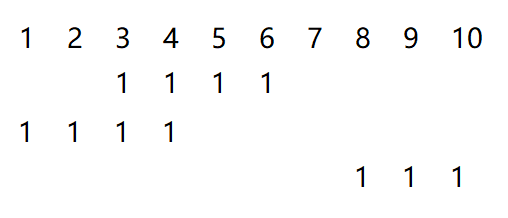

第一行是下标，下面是修改，设用修改建出的线性基大小为 $si$ ，不难发现用这些修改所能搞出的排列个数就是 $2^{si}$ ，直接维护线性基，每次加入操作是 $O(\frac{n^2}{w})$ ，求一个 $f(i)$ 的时间是 $O(m \frac{n^2}{w})$ ，这还要乘 $i$ 的个数 $\log v$ ，直接爆炸

考虑本题的特殊性质，发现 $1$ 都是连续的，考虑差分，即把“ $000111100$ ”变成“ $000100010$ ”，不难发现它们异或差分是一一对应的，个数不变，那么每次就只需要更改两个位置，单次变成 $O(\frac{2n}{w})$ ，但好像还是不行

再考虑每个数只有两个 $1$ 的特殊性质，发现这就是个联通性，把每个位当作一个点，每次操作就是向两个点之间连边，如果某次操作加入前那两个点已经联通了，就说明这次操作加入的数可以被表示（具体表示方法就是沿着两点间的路径把经过的值权异或起来），那么线性基大小不变，用并查集维护联通性，单次操作 $O(\alpha(n))$ ；至此，总时间为 $O(m \alpha(n) \log v)$ ，可以得 $80pts$

发现得不了满分的原因是 $v$ 的范围太阴间，注意到若加入边时，端点已连通，那么可以用新加的边去替换环上的某条边，显然将 $v$ 更小的替换掉，就能保证不变劣，用 LCT 对 $n + 1$ 个点维护一个关于边权 $v_i$ 的最大生成树即可，时间复杂度 $O(n \log n )$

题都没有，代码当然咕咕咕了（幸好不用打）