还是卡特兰数简单一点……

斯特林数

第一类斯特林数

定义

第一类斯特林数（Stirling）分为无符号第一类斯特林数 $s_s(n, m)$ 和带符号第一类斯特林数 $s_u(n, m)$ ，有无符号斯特林数分别表现为其升阶函数和降阶函数的各项系数（反正我是没看懂），形式如下：
$$
\begin{aligned}
x^{n\uparrow} = x(x + 1)(x + 2)…(x + n - 1) = \sum_{k = 0}^{n}s_u(n, k)x^k\\
x^{n\downarrow} = x(x - 1)(x - 2)…(x - n + 1) = \sum_{k = 0}^{n}s_s(n, k)x^k\\
\end{aligned}
$$
对于有无符号斯特林数之间的关系有 $s_s(n, m) = (-1)^{n + m}s_u(n, m)$

组合数学中的第一类斯特林数一般指无符号的第一类斯特林数，以下的“第一类斯特林数”若无特殊说明，也指“无符号的第一类斯特林数”，无符号的第一类斯特林数还有一个组合数学上的定义，为： $n$ 个不同元素构成 $m$ 个圆排列（两个圆排列间没有顺序之分）的方案数，记作 $s(n, m)$ 或 ${n \brack m}$

求法

第一类斯特林数有一个递推式：
$$
{n \brack m} = {n - 1 \brack m - 1} + (n - 1){n - 1 \brack m}
$$
证明：

考虑第一类斯特林数的定义，${n \brack m}$ 表示把 $n$ 个不同元素构成 $m$ 个圆排列的方案数，对于第 $n$ 个数，若它单独成为新的一个圆，则它前面的 $n - 1$ 个数构成了 $m - 1$ 个圆，方案数为 ${n - 1 \brack m - 1}$ ；若它加入到前面构成的圆中，则它前面的 $n - 1$ 个数构成了 $m$ 个圆，方案数为 ${n - 1 \brack m}$ ，而这 $n - 1$ 个数间有 $n - 1$ 空位可以选择，共 $(n - 1){n - 1 \brack m}$ 种方案

两种情况综合，即得递推式

代码：

#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int N = 1e4 + 5, P = 1e9 + 7;
int n, m;
int s[N][N];
int main()
{
	scanf("%d%d", &n, &m);
	s[0][0] = 1;
	for (int i = 1; i <= n; ++i)
		for (int j = 1; j <= m; ++j)
			s[i][j] = (s[i - 1][j - 1] + (LL)(i - 1) * s[i - 1][j]) % P;
	printf("%d\n", s[n][m]);
	return 0;
}

性质

• ${0 \brack 0} = 1$
• ${n \brack 0} = 0$
• ${n \brack n} = 1$

以上三条由定义不难得到

• ${n \brack 1} = (n - 1)!$

• ${n \brack n - 1} = \binom{n}{2}$

证明：

依然考虑定义，$n$ 个不同元素构成 $n - 1$ 个圆排列，必然有一个圆排列有两个数，其它圆排列只有一个数，有两个数的圆排列有 $\binom{n}{2}$ 种方案，对应其它都只有一种方案

• $\sum_{k = 0}^{n} {n \brack k} = n!$

证明：

令升阶函数中的 $x = 1$ ，即得原式

第二类斯特林数

定义

第二类斯特林数实际上是集合的一个拆分，表示将 $n$ 个不同的元素划分成 $m$ 个集合（两个集合间没有顺序之分）的方案数，记为 $S(n, m)$ 或 ${n \brace m}$ ，和第一类斯特林数不同的是，集合内是不考虑次序的，而圆排列是有序的

求法

递推式：
$$
{n \brace m} = {n - 1 \brace m - 1} + m {n - 1 \brace m}
$$
还是考虑定义，将 $n$ 个不同的元素划分成 $m$ 个集合，对于第 $n$ 个数，可以单独为一个集合，则前面 $n - 1$ 个数构成 $m - 1$ 个集合，方案数为 ${n - 1 \brace m - 1}$ ；也可以加入到原有集合中，则前面 $n - 1$ 个数构成 $m$ 个集合，方案数为 ${n - 1 \brace m}$ ，而第 $n$ 个数在 $m$ 个集合中选一个加入，方案数为 $m$

两种情况综合，即得递推式

#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int N = 1e4 + 5, P = 1e9 + 7;
int n, m;
int S[N][N];
int main()
{
	scanf("%d%d", &n, &m);
	S[0][0] = 1;
	for (int i = 1; i <= n; ++i)
		for (int j = 1; j <= m; ++j)
			S[i][j] = (S[i - 1][j - 1] + (LL)j * S[i - 1][j]) % P;
	printf("%d\n", S[n][m]);
	return 0;
}

计算式：
$$
{n \brace m} = \frac{1}{m!} \sum_{k = 0}^{m} (-1)^k \binom{m}{k} (m - k)^n
$$
证明见百度百科

性质

• ${n \brace 0} = 0^n$
• ${n \brace 1} = 1$
• ${n \brace n} = 1$
• ${n \brace 2} = 2^{n - 1} - 1$
• ${n \brace n - 1} = \binom{n}{2}$
• $\sum_{k = 0}^{n} {n \brace k} = B_n$ ，其中 $B_n$ 是贝尔数

两类斯特林数的关系

其实就一个：
$$
\sum_{k = 0}^{n} {n \brace k}{k \brack m} = \sum_{k = 0}^{n} {n \brack k}{k \brace m}
$$

例题

建筑师

以高度为 $n$ 的建筑为分界线，左边选择 $A - 1$ 个建筑让他们可以被看见，右边 $B - 1$ 个，如图：

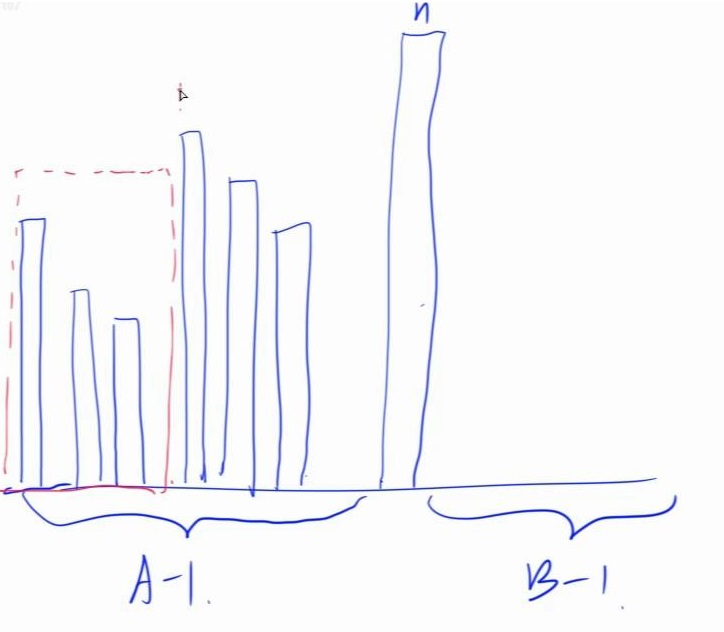
问题转化为将 $1 \sim n - 1$ 划分为 $A + B - 2$ 部分（即红框里的），对于每一个部分，将其中元素排成一个圆排列，放置时保证最高的在最左边（如果是放在 $n$ 右边，则最高的在最右边），故有 ${n \brack m}$ 种方案

然后将这些部分划分给 $n$ 两边，有 $\binom{A + B - 2}{A - 1}$ 种方案

#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int N = 5e4 + 5, P = 1e9 + 7, M = 200 + 5;
int s[N][M], C[M][M];
void pred()
{
	s[0][0] = 1;
	for (int i = 1; i < N; ++i)
		for (int j = 1; j < M; ++j)
			s[i][j] = (s[i - 1][j - 1] + (LL)(i - 1) * s[i - 1][j]) % P;
	for (int i = 0; i < M; ++i)
		for (int j = 0; j <= i; ++j)
			if (!j)
				C[i][j] = 1;
			else
				C[i][j] = (C[i - 1][j] + C[i - 1][j - 1]) % P;
}
int main()
{
	pred();
	int T, n, a, b;
	scanf("%d", &T);
	while (T--)
	{
		scanf("%d%d%d", &n, &a, &b);
		printf("%d\n", (LL)s[n - 1][a + b - 2] * C[a + b - 2][a - 1] % P);
	}
	return 0;
}