Dyd's Blog

He who has a strong enough why can bear almost any how.

Tarjan缩点

Posted on Edited on In
Symbols count in article: 6.4k Reading time ≈ 6 mins.

辣个男银太讨厌了！

Tarjan缩点

割点与桥

给定无向连通图 $G=(V,E)$ ：
若对于 $x \in V$ ，从图中删去节点 $x$ 及其所以连边后， $G$ 分裂成两个及以上不连通的子图，则称 $x$ 为 $G$ 的割点；
若对与 $e \in E$ ，从图中删去 $e$ 后， $G$ 分裂为两个（也只可能分裂成两个）不连通的子图，则称 $e$ 为 $G$ 的割边或桥。

由Robert Tarjan的名字命名的Tarjan算法可以在线性时间内求无向图的割点与桥，进一步可以求出双连通分量。

时间戳与追溯值

“时间戳”的概念比较简单，就是在dfs搜索时按搜索顺序对每个节点编号，一般记作 $dfn[x]$
在dfs遍历时，经过的边被定义为“搜索树”中的边，如图，红色为“搜索树”中的边，点中的数字为时间戳：
搜索树
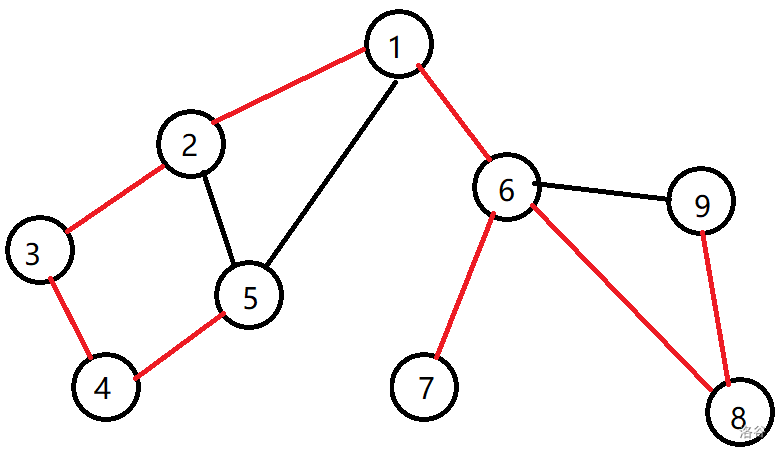
Tarjan算法又引入了一个”追溯值”，记作 $low[x]$ 。定义 $low[x]=\min (dfn[y])$ ，其中 $y$ 为满足下列两个条件之一的节点:

  1. $y$ 在 $x$ 的子树中（包括 $x$ 本身）

  2. $y$ 通过1条不在搜索树上的边，能够到达 $x$ 的子树（包括 $x$ 本身）

可以感性地将追溯值理解为从点 $x$ 出发，不走先前走过的点，可以到达的时间戳最小的点的时间戳
下图用绿色数字标出了每个点的追溯值：
追溯值
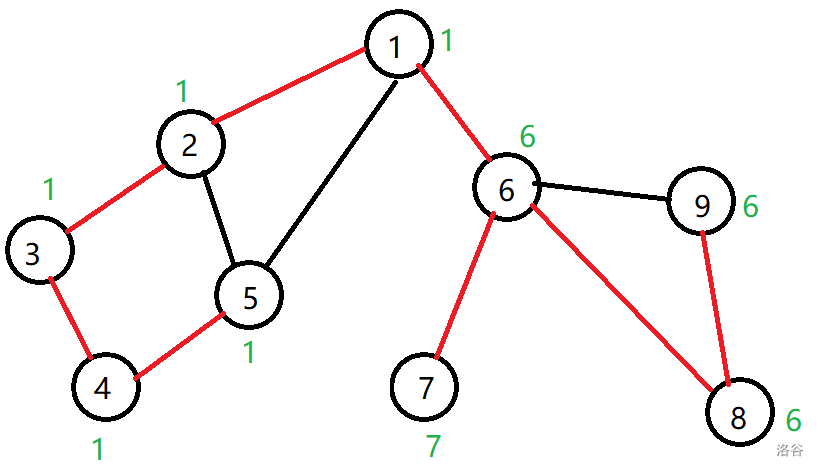
根据定义，可以这样计算计算 $low[x]$ ：

  • 令 $low[x]=dfn[x]$ （因为 $x$ 的时间戳一定是它所在子树中最小的）

  • 枚举每条边 $(x,y)$ ：

  1. 若搜索树上 $x$ 是 $y$ 的父亲， 递归计算 $y$ ，然后令 $low[x]=\min (low[x],low[y])$

  2. 若 $(x,y)$ 不在搜索树上，令 $low[x]=\min (low[x],dfn[y])$

桥（割边）的判断

无向边 $(x,y)$ 是桥，当且仅当 $(x,y)$ 在搜索树上（设 $x$ 为父节点），且满足 $dfn[x]<low[y]$

正确性显然：若 $dfn[x]<low[y]$ ，说明从 $y$ 出发，不走 $(x,y)$ ，不管如何走都无法到达比 $x$ 更早遍历的点，所以只要删除 $(x,y)$ ， $y$ 及其子树就与比 $x$ 早遍历的点分隔开了，故 $(x,y)$ 为割边，反之则不是。
下图中桥用虚线标出：
桥
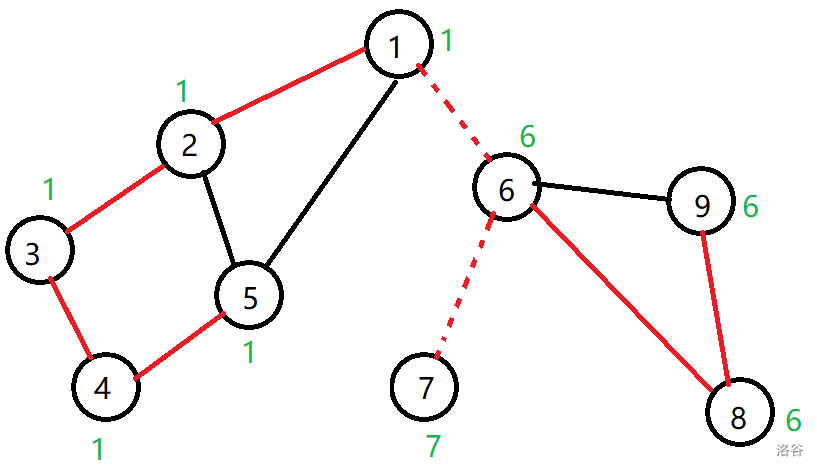
不难发现：桥一定是搜索树中的边，且一个简单环中的边一定不是桥。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
int n,m;
struct Edge{
    int ne,ver;
}e[N<<1];
int h[N],idx=0;
int dfn[N],low[N],num=0;
bool bridge[N<<1];
void add(int x,int y){
    e[idx].ver=y,e[idx].ne=h[x],h[x]=idx++;
}
void tarjan(int x,int in_e){
    dfn[x]=low[x]=++num;
    for(int i=h[x],y;i!=-1;i=e[i].ne){
        y=e[i].ver;
        if(!dfn[y]){
            tarjan(y,i);
            low[x]=min(low[x],low[y]);
            if(low[y]>dfn[x]) bridge[i]=bridge[i^1]=true;
        }
        else if(i!=(in_e^1)) low[x]=min(low[x],dfn[y]);
    }
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=0;i<=n;++i) h[i]=-1;
    for(int i=1,u,v;i<=m;++i){
        scanf("%d%d",&u,&v);
        add(u,v);
        add(v,u);
    }
    for(int i=1;i<=n;++i)
        if(!dfn[i]) tarjan(i,-1);
    for(int i=0;i<idx;i+=2)
        if(bridge[i]) printf("%d %d\n",e[i^1].ver,e[i].ver);
    return 0;
}

割点的判断

若 $x$ 不是搜索树的根，则 $x$ 是割点当且仅当存在 $x$ 的一个子节点 $y$ 满足 $dfn[x] \le low[y]$ ，特别的，当 $x$ 为搜索树的根时，需要有至少两个子节点 $y_1,y_2$ 满足条件
证明方法同上，下图用蓝色标出了两个割点，它们的时间戳分别是1和6：
割点
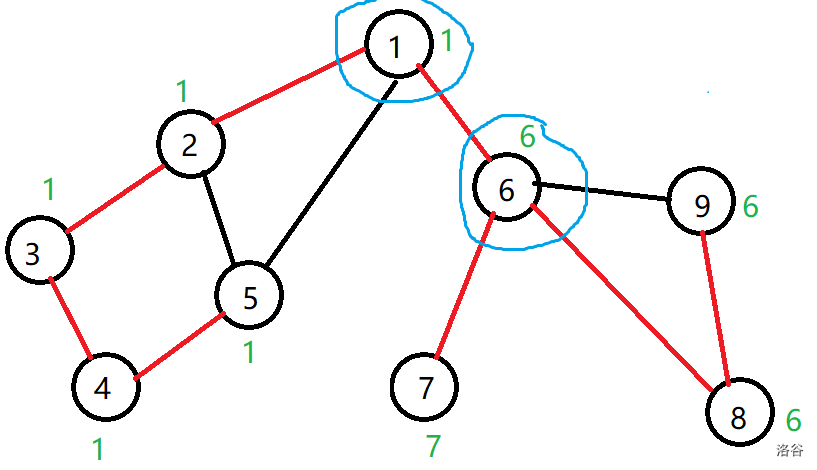
值得注意的是，在判断割点时，由于是小于等于号，所以不必像桥一样考虑重边和父节点，但要比桥多判一个自环。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
int n,m;
struct Edge{
    int ne,ver;
}e[N<<1];
int h[N],idx=0;
int dfn[N],low[N],num=0;
bool cut[N];
int root;
void add(int x,int y){
    e[idx].ver=y,e[idx].ne=h[x],h[x]=idx++;
}
void tarjan(int x){
    dfn[x]=low[x]=++num;
    int f=0;
    for(int i=h[x],y;i!=-1;i=e[i].ne){
        y=e[i].ver;
        if(!dfn[y]){
            tarjan(y);
            low[x]=min(low[x],low[y]);
            if(low[y]>=dfn[x]){
            	++f;
            	if(x!=root||f>1) cut[x]=true;
            }
        }
        else low[x]=min(low[x],dfn[y]);
    }
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=0;i<=n;++i) h[i]=-1;
    for(int i=1,u,v;i<=m;++i){
        scanf("%d%d",&u,&v);
        if(u==v) continue; //判自环 
        add(u,v);
        add(v,u);
    }
    for(int i=1;i<=n;++i)
        if(!dfn[i]) root=i,tarjan(i);
    for(int i=1;i<=n;++i)
        if(cut[i]) printf("%d ",i);
    return 0;
}

无向图的双连通分量

若无向图 $G$ 不存在割点，即其中任意两点间都有至少两条简单路径满足两条路径上的点集的并中只存在起点和终点，则称 $G$ 为“点双连通图”。

类似的，若无向图 $G$ 不存在桥，即其中任意两点间都有至少两条简单路径满足两条路径上的边集的并为空集，则称 $G$ 为“边双连通图”。

如图，图一是“点双连通图”而不是“边双连通图”，图二相反：
范例
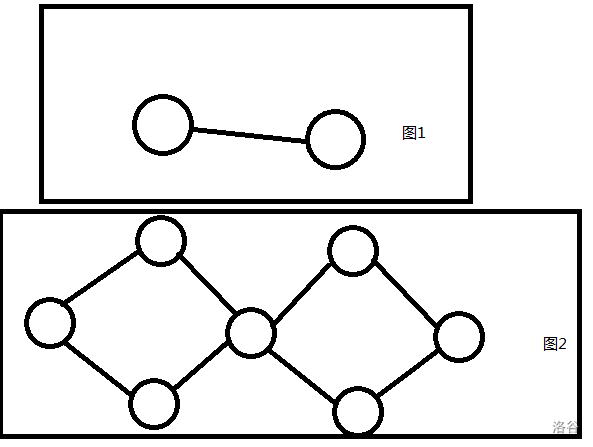
无向图的“极大”点双连通子图称为“点双连通分量”，记作“v-DCC”；无向图的“极大”边双连通子图称为“边双连通分量”，记作“e-DCC”
在以上定义中，一个双连通子图 $G$ 定义为“极大”是指不存在一个双连通子图 ${G}’$ 使得 $G$ 是它的子图

边双连通分量

e-DCC比较好求，只需删除所有桥，无向图就会分裂成若干e-DCC
代码（加到求桥的代码中）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
......
int c[N],dcc;
void dfs(int x){
	c[x]=dcc;
	for(int i=h[x],y;i!=-1;i=e[i].ne){
		y=e[i].ver;
		if(c[y]||bridge[i]) continue;
		dfs(y);
	}
}
int main(){
	......
    for(int i=1;i<=n;++i)
    	if(!c[i]){
    		++dcc;
    		dfs(i);
    	}
    printf("the num of e-DCC is %d\n",dcc);
    for(int i=1;i<=n;++i)
    	printf("%d blongs to e-DCC %d\n",i,c[i]);
    return 0;
}

e-DCC的缩点就是把每个e-DCC看作一个新的点，用桥将新的点连起来，构成一棵树（或森林），在上面代码中再加入这段代码，可以实现e-DCC缩点：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
......
struct Edge{
    int ne,ver;
}ec[N<<1];
int hc[N<<1],idc=0;
void add_c(int x,int y){
	ec[idc].ver=y,ec[idc].ne=hc[x],hc[x]=idc++;
}
int main(){
	......
    for(int i=0;i<=n;++i) hc[i]=-1;
	......
	for(int i=0,x,y;i<idx;i+=2){
		x=e[i].ver,y=e[i^1].ver;
		if(c[x]==c[y]) continue;
		add_c(c[x],c[y]);
		add_c(c[y],c[x]);
	}
	printf("缩点后的森林，点数：%d，边数（可能有重边）：%d\n",dcc,(idc+1)/2);
	for(int i=0;i<idc;i+=2)
		printf("%d %d\n",ec[i].ver,ec[i^1].ver);
    return 0;
}

点双连通分量

根据v-DCC的定义，除孤立点外，v-DCC的大小至少为二，且每个割点至少属于两个不同的点双连通分量，在求割点的代码中加入一个栈可以求出v-DCC（下面的代码不用加在之前代码前）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
int n,m;
struct Edge{
    int ne,ver;
}e[N<<1];
int h[N],idx=0;
int dfn[N],low[N],num=0;
bool cut[N];
int root;
int stk[N],top=0,cnt=0;
vector<int>dcc[N];
void add(int x,int y){
    e[idx].ver=y,e[idx].ne=h[x],h[x]=idx++;
}
void tarjan(int x){
    dfn[x]=low[x]=++num;
    stk[++top]=x; //栈记录经过的节点
	if(x==root&&h[x]==-1){ //孤立点 
		dcc[++cnt].push_back(x);
		return ;
	} 
    int f=0;
    for(int i=h[x],y;i!=-1;i=e[i].ne){
        y=e[i].ver;
        if(!dfn[y]){
            tarjan(y);
            low[x]=min(low[x],low[y]);
            if(low[y]>=dfn[x]){
            	++f;
            	if(x!=root||f>1) cut[x]=true;
            	++cnt;
            	int z;
            	do{
            		z=stk[top--];
            		dcc[cnt].push_back(z);
            	}while(z!=y);
            	dcc[cnt].push_back(x);
            }
        }
        else low[x]=min(low[x],dfn[y]);
    }
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=0;i<=n;++i) h[i]=-1;
    for(int i=1,u,v;i<=m;++i){
        scanf("%d%d",&u,&v);
        if(u==v) continue; //判自环 
        add(u,v);
        add(v,u);
    }
    for(int i=1;i<=n;++i)
        if(!dfn[i]) root=i,tarjan(i);
	for(int i=1;i<=cnt;++i){
		printf("v-DCC %d: ",i);
		for(int j=0;j<dcc[i].size();++j) printf("%d ",dcc[i][j]);
		puts("");
	}
    return 0;
}

与e-DCC不同，由于每一个割点会包含在不同的v-DCC中，所以对于一个有 $p$ 个割点和 $t$ 个v-DCC的图，其缩点后的图包含 $p+t$ 个节点，由 $p$ 个割点将图连通，构成一棵树（或森林），如图：
v-DCC
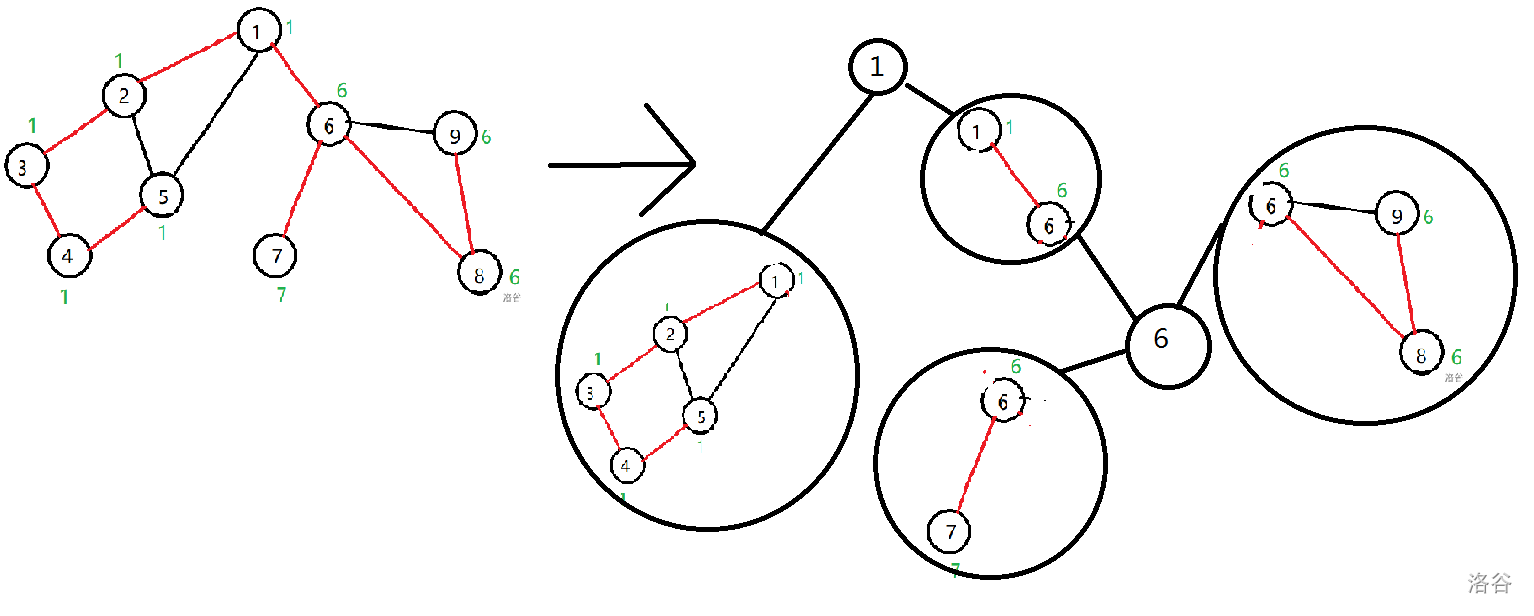
代码如下（插在上面的代码中）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
......
int new_id[N],c[N]; 
struct Edge{
	int ne,ver;
}ec[N<<1];
int hc[N<<1],idc=0;
void add_c(int x,int y){
	ec[idc].ver=y,ec[idc].ne=hc[x],hc[x]=idc++;
}
int main(){
    ......
    for(int i=0;i<=n;++i) hc[i]=-1;
	//给每个割点一个编号，从cnt+1开始 
	int id=cnt;
	for(int i=1;i<=n;++i)
		if(cut[i]) new_id[i]=++id; 
	//建图，用割点连接v-DCC
	for(int i=1;i<=cnt;++i)
		for(int j=0,x;j<dcc[i].size();++j){
			x=dcc[i][j];
			if(cut[x]){
				add_c(i,new_id[x]);
				add_c(new_id[x],i);
			}
			else c[x]=i; //割点外的点只属于1个v-DCC 
		}
	printf("缩点后的森林，点数：%d，边数：%d\n",id,(idc+1)/2);
	for(int i=0;i<idc;i+=2)
		printf("%d %d\n",ec[i].ver,ec[i^1].ver); 
    return 0;
}

nice!终于写完了！