Dyd's Blog

He who has a strong enough why can bear almost any how.

Splay

Posted on Edited on In
Symbols count in article: 6.7k Reading time ≈ 6 mins.

真正好打的平衡树

Splay

首先是Splay的定义，上代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
struct Splay{
	int ch[2];	//左右儿子
	int fa;		//父节点
	int v;		//值
	int size;	//儿子数量
	int tag;	//懒标记
	int cnt;	//值等于v的数都建成一个点,故记录数量
	void init(int _v,int _fa){		//初始化
		ch[0]=ch[1]=0;
	 	v=_v;
		fa=_fa;
		tag=0;
		size=1;
		cnt=1;
	 	return ;
	}
}tr[N];

Splay的基本操作是旋转，在保证中序遍历不变的情况下，通过旋转将树的结构改变，如下图中 $x$ 、 $y$ 、 $z$ 是三个节点，而 $A$ 、 $B$ 、 $C$ 是三棵子树，在将 $x-y$ 左右旋转后，树的结构发生变化：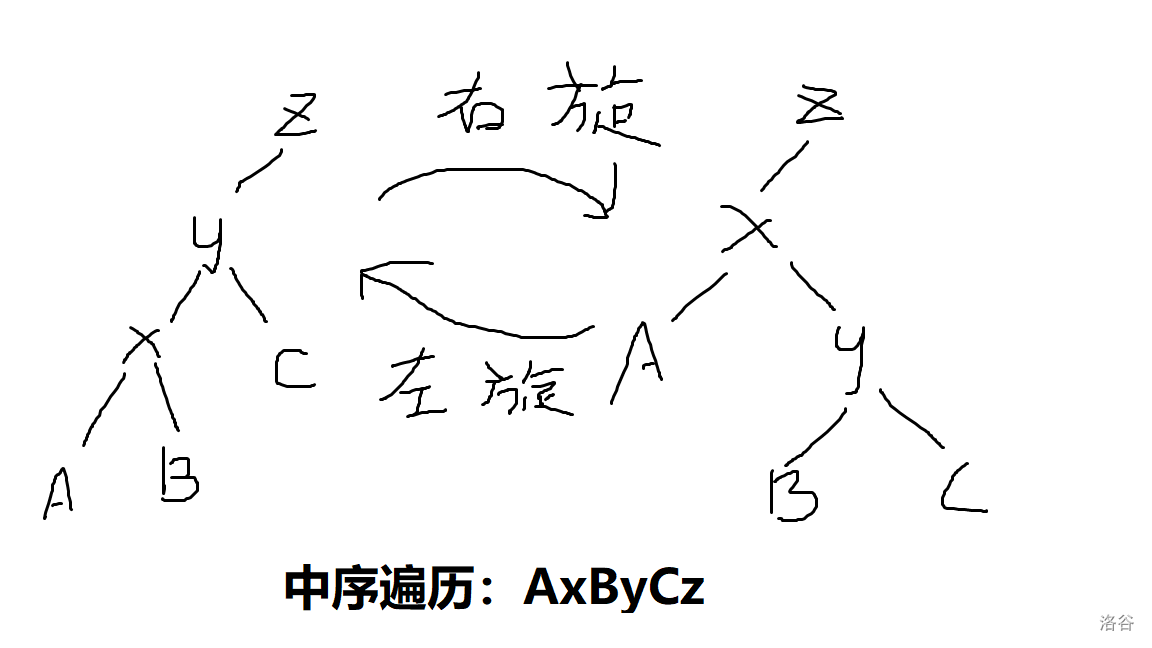
旋转
如上图中，将 $x-y$ 右旋，那么 $z$ 就完全不动，而旋转后我们发现 $A$ 、 $B$ 、 $y$ 都成了 $x$ 的子节点，这显然不满足BST性质。为了满足BST，我们比较三个子节点（子树），发现由BST性质，有 $A<x<B<y<C$ ，明显，为了BST性质，只能让 $A$ 继续做 $x$ 的左子树，将 $B$ 、 $y$ 、 $C$ 构造成 $x$ 的右子树。
具体实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
//计算x的儿子数量
void push_up(int x){
	tr[x].size=tr[tr[x].ch[0]].size+tr[tr[x].ch[1]].size+tr[u].cnt;
	return ;
}
//旋转
void rotate(int x){
	int y=tr[x].fa;int z=tr[y].fa;
    //k=0表示x是y的左儿子,k=1表示x是y的右儿子
	int k=tr[y].ch[1]==x;
    //把x变成z的儿子
	tr[z].ch[tr[z].ch[1]==y]=x,tr[x].fa=z;
    //把x的一个儿子改为y的儿子,具体哪个儿子看最初x是y的哪个儿子,就改成相同的儿子
	tr[y].ch[k]=tr[x].ch[k^1],tr[tr[x].ch[k^1]].fa=y;
    //把y变成x的儿子,具体哪个儿子看最初x是y的哪个儿子,就改成相反的儿子
	tr[x].ch[k^1]=y,tr[y].fa=x;
   //重新计算x、y
	push_up(y),push_up(x);
	return ; 
}

而在Splay中我们插入、修改、删除任何一个节点的方式就是将该节点转至根节点，再进行操作。
为将节点 $x$ 转至根节点，我们定义函数 $Splay(x,k)$ 表示将节点 $x$ 转至节点 $k$ 下方（即 $x$ 是 $k$ 的子节点），通过 $Splay(x,0)$ ，我们可以将 $x$ 转至根节点。
而为了实现该函数，我们发现有如下两类情况（以下我们设 $y$ 是 $x$ 的父节点， $z$ 是 $y$ 的父节点）：

  1. $x$ 、 $y$ 、 $z$ 在同一直线，如图：共线

  2. $x$ 、 $y$ 、 $z$ 不在同一直线，如图：不共线

而对于这两种情况，我们也有不同的策略：

  1. 先转一次 $y$ ，再转一次 $x$ （具体方向取决于是左儿子还是右儿子）如图：c1

  2. 连转两次 $x$ （具体方向取决于是左儿子还是右儿子）如图：c2

代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void splay(int x,int k){
	//if(x==k) return ;
 	while(tr[x].fa!=k){
		int y=tr[x].fa;int z=tr[y].fa;
		if(z!=k)
        	//若是折线关系,先转一次x,否则先转一次y
			(tr[y].ch[1]==x)^(tr[z].ch[1]==y)?rotate(x):rotate(y); 
        //无论如何第二次都转x
		rotate(x);
	}
    //若k=0,说明x是根节点
	if(!k) root=x;
	return ;
}

在实现 $Splay()$ 后，我们就可以完成操作。

插入

将一个数 $x$ 插入到Splay中：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void insert(int x){
	int u=root,ff=0;
    //找到x的位置u和其父节点ff
	while(u&&tr[u].v!=x) ff=u,u=tr[u].ch[x>tr[u].v];
    //若已存在,个数加1
	if(u) t[u].cnt++;
    //否则新建节点
	else{
		u=++idx;
		if(ff) tr[ff].ch[x>tr[ff].v]=u;
		tr[u].init(x,ff);
	}
    //优化:每次都让新加入的点为根
	splay(u,0);
	return ;
}

查找第k个数

找到第 $k$ 大的数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int get_k(int k){
	int u=root;
	if(tr[u].size<k) return -1;
	while(1){
		push_down(u);
		int y=t[u].ch[0];
        //若k在u的后面,直接减掉u及前面的数,进入右子树
		if(k>tr[y].size+tr[u].cnt) k-=tr[y].size+tr[u].cnt,u=tr[u].ch[1];
        //若u的左子树的节点数大于k,说明k在左子树中
		else if(tr[y].size>=k) u=y;
        //否则第k个就是u
		else return tr[u].v;
	}
	return -1;
}

查找x的位置

该函数可以把数 $x$ 转到根节点，完成后x的排名就是
$tr[tr[root].ch[0]].size+1 \sim tr[tr[root].ch[0]].size+tr[root].cnt$

1
2
3
4
5
6
7
void find(int x){
	int u=root;
	if(!u) return ;		//不存在节点
    //找到x所在的位置u
	while(tr[u].ch[x>tr[u].v]&&x!=tr[u].v) u=tr[u].ch[x>tr[u].v];
	splay(u,0);
}

查找前驱/后继

该函数可以找到数 $x$ 的前驱（ $f=0$ ）或后继（ $f=1$ ）（大小关系严格）：

1
2
3
4
5
6
7
8
9
10
11
int near(int x,int f){
	find(x);
	int u=root;
	if((tr[u].v>x&&f)||(tr[u].v<x&&!f)) return u;
    //若不严格，用if((tr[u].v>x&&f)||(tr[u].v<x&&!f)||(tr[u].v==x&&tr[u].cnt>1)) return u;
    //进入左/右子树
	u=tr[u].ch[f];
    //找到该子树中的最大/小值,方法是一直向与f相反的方向走
	while(tr[u].ch[f^1]) u=tr[u].ch[f^1];
	return u;
}

删除数x

在Splay中删除 $x$ ：

1
2
3
4
5
6
7
8
9
10
int remove(int x){
	int last=near(x,0);		//前驱
	int next=near(x,1);		//后继
	splay(last,0);
	splay(next,last);
    //x此时就是next的左儿子
	int rem=tr[next].ch[0];
	if(tr[rem].cnt>1) tr[rem].cnt--,splay(rem,0);
	else tr[next].ch[0]=0;
}

中序输出

1
2
3
4
5
6
7
void midout(int u){
	push_down(u);
	if(tr[u].ch[0]) midout(tr[u].ch[0]);
	if(tr[u].v>1&&tr[u].v<n+2) printf("%d ",tr[u].v-1);
	if(tr[u].ch[1]) midout(tr[u].ch[1]);
	return ;
}

下传懒标记

以下用区间翻转举例：

1
2
3
4
5
6
7
8
9
void push_down(int x){
	if(tr[x].tag){
		tr[tr[x].ch[0]].tag^=1;
		tr[tr[x].ch[1]].tag^=1;
		tr[x].tag=0;
		swap(tr[x].ch[0],tr[x].ch[1]);
	}
	return ;
}

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
#include<bits/stdc++.h>
using namespace std;
const int N=5e5+5,INF=0x3f3f3f3f;
int n,m;
struct Splay{
	int ch[2];
	int fa;
	int v;
	int size;
	int tag;
	int cnt;
	void init(int _v,int _fa){
		ch[0]=ch[1]=0;
	 	v=_v;
		fa=_fa;
		tag=0;
		size=1;
		cnt=1;
	 	return ;
	}
}tr[N];
int root=0,idx=0;
void push_down(int x){
	if(tr[x].tag){
		tr[tr[x].ch[0]].tag^=1;
		tr[tr[x].ch[1]].tag^=1;
		tr[x].tag=0;
		swap(tr[x].ch[0],tr[x].ch[1]);
	}
	return ;
}
void push_up(int x){
	tr[x].size=tr[tr[x].ch[0]].size+tr[tr[x].ch[1]].size+tr[x].cnt;
	return ;
}
void rotate(int x){
	int y=tr[x].fa;int z=tr[y].fa;
	int k=tr[y].ch[1]==x;
	tr[z].ch[tr[z].ch[1]==y]=x,tr[x].fa=z;
	tr[y].ch[k]=tr[x].ch[k^1],tr[tr[x].ch[k^1]].fa=y;
	tr[x].ch[k^1]=y,tr[y].fa=x;
	push_up(y),push_up(x);
	return ; 
}
void splay(int x,int k){
	if(x==k) return ;
	while(tr[x].fa!=k){
		int y=tr[x].fa;int z=tr[y].fa;
		if(z!=k)
			(tr[y].ch[1]==x)^(tr[z].ch[1]==y)?rotate(x):rotate(y); 
		rotate(x);
	}
	if(!k) root=x;
	return ;
}
void find(int x){
	int u=root;
	if(!u) return ;
	while(tr[u].ch[x>tr[u].v]&&x!=tr[u].v) u=tr[u].ch[x>tr[u].v];
	splay(u,0);
}
int near(int x,bool f){
	find(x);
	int u=root;
	if((tr[u].v>x&&f)||(tr[u].v<x&&!f)) return u;
	u=tr[u].ch[f];
	while(tr[u].ch[f^1]) u=tr[u].ch[f^1];
	return u;
}
int remove(int x){
	int last=near(x,0);
	int next=near(x,1);
	splay(last,0);
	splay(next,last);
	int rem=tr[next].ch[0];
	if(tr[rem].cnt>1) tr[rem].cnt--,splay(rem,0);
	else tr[next].ch[0]=0;
}
void insert(int x){
	int u=root,ff=0;
	while(u&&tr[u].v!=x) ff=u,u=tr[u].ch[x>tr[u].v];
	if(u) tr[u].cnt++;
	else{
		u=++idx;
		if(ff) tr[ff].ch[x>tr[ff].v]=u;
		tr[u].init(x,ff);
	}
	splay(u,0);
	return ;
}
int get_k(int k){
	int u=root;
	if(tr[u].size<k) return -1;
	while(1){
		push_down(u);
		int y=tr[u].ch[0];
		if(k>tr[y].size+tr[u].cnt) k-=tr[y].size+tr[u].cnt,u=tr[u].ch[1];
		else if(tr[y].size>=k) u=y;
		else return tr[u].v;
	}
	return -1;
}
void midout(int u){
	push_down(u);
	if(tr[u].ch[0]) midout(tr[u].ch[0]);
	if(tr[u].v>1&&tr[u].v<n+2) printf("%d ",tr[u].v-1);		//视具体情况 
	if(tr[u].ch[1]) midout(tr[u].ch[1]);
	return ;
}
int main(){
	insert(x);
	remove(x);
	find(x);
	get_k(x+1);	//编号要加1
	near(x,0); 
	near(x,1);
	midout(root);
	//P3369
/*	scanf("%d",&n);
	//注意要多插入两个数 
	insert(-INF);
	insert(INF);
	while(n--){
		int op,x;
		scanf("%d%d",&op,&x);
		if(op==1) insert(x);
		else if(op==2) remove(x);
		else if(op==3) find(x),printf("%d\n",tr[tr[root].ch[0]].size);
		else if(op==4) printf("%d\n",get_k(x+1));
		else if(op==5) printf("%d\n",tr[near(x,0)].v);
		else printf("%d\n",tr[near(x,1)].v);
	}
*/
	//P3391
/*
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n+2;++i) insert(i);	//增加两个点防止越界 
	while(m--){
		int l,r;
		scanf("%d%d",&l,&r);
		l=get_k(l),r=get_k(r+2); 
		splay(l,0);splay(r,l);
		tr[tr[tr[root].ch[1]].ch[0]].tag^=1;
	}
	midout(root);
	printf("\n");
*/ 
	return 0;
}