Dyd's Blog

He who has a strong enough why can bear almost any how.

SBT（Size Balanced Tree）

Posted on Edited on In
Symbols count in article: 8.5k Reading time ≈ 8 mins.

cqf大佬智慧的结晶

SBT

简介

SBT（子树大小平衡树）是一种通过子树大小来维持平衡的平衡树，由cqf大佬发明，是一种非常非常优秀的平衡树（反正比Splay快），与Splay的旋转类似，它通过旋转来平衡，但不同的是，Splay的旋转没有条件，而SBT的旋转是为了维护一个有关子树大小的性质。

定义

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
struct SBT{
    int v; //价值关键字
    int size; //子树大小
    int l,r; //左右儿子
    void inint(int _v){
        v=_v;
        size=1;
        l=r=0;
    }
#define v(i) tr[i].v
#define size(i) tr[i].size
#define l(i) tr[i].l
#define r(i) tr[i].r
}tr[N];
int cnt=0，root;

旋转

SBT的旋转与Splay类似，但略有不同，主要表现在它不记录父节点，而是通过传实参来更新与 $Z$ 的关系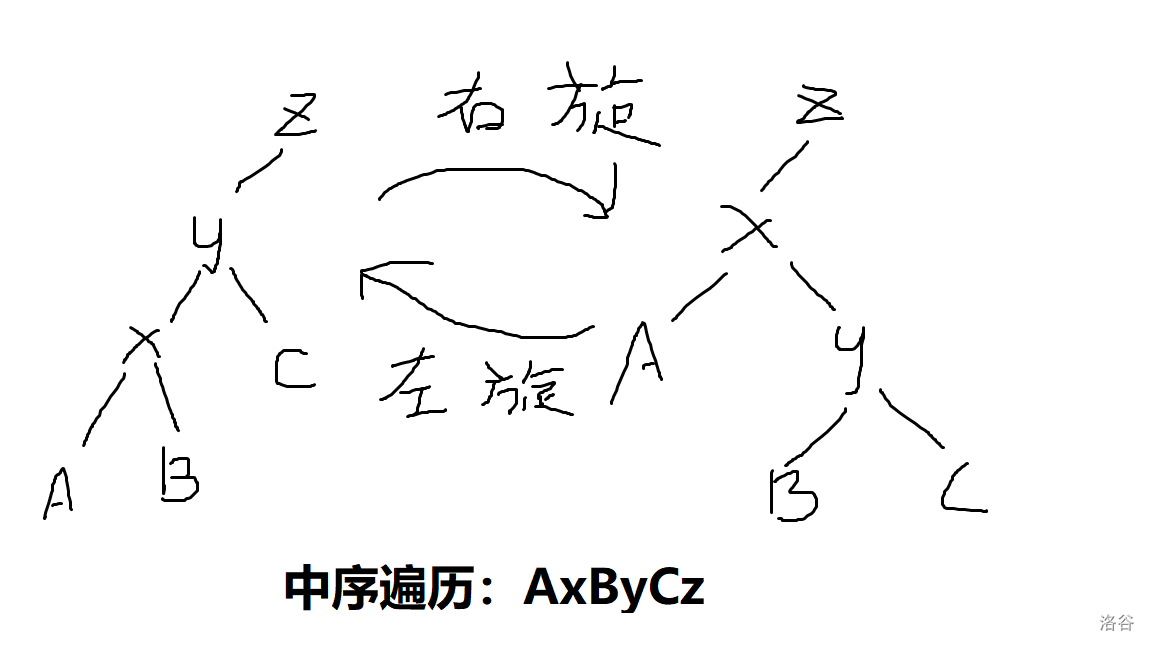
旋转
代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void r_rotate(int &t){ //右旋
    int k=l(t);
    l(t)=r(k);
    r(k)=t;
    //代替Splay的push_up
    size(k)=size(t);
    size(t)=size(l(t))+size(r(t))+1;
    //更新z的儿子
    t=k;
}
void l_rotate(int &t){ //左旋
    int k=r(t);
    r(t)=l(k);
    l(k)=t;
    size(k)=size(t);
    size(t)=size(l(t))+size(r(t))+1;
    t=k;
}

性质

SBT和Splay的主要不同点是SBT维护了两个性质：

  1. $size(r(t)) \ge size(l(l(t)))\ ,\ size(r(l(t)))$

  2. $size(l(t)) \ge size(r(r(t)))\ ,\ size(l(r(t)))$

如图，就是说：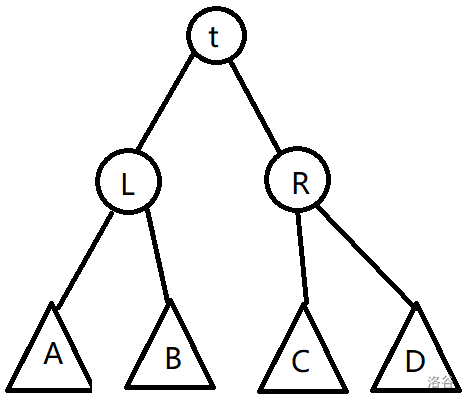
SBT性质

  1. $size(R) \ge size(A)\ ,\ size(B)$

  2. $size(L) \ge size(C)\ ,\ size(D)$

而为了在插入新节点后仍保持该性质，我们需要“机智”地旋转，假设我们用一个函数（命名为 $maintain(t)$ ）可以做到使 $t$ 和它的子树符合以上性质，我们来考虑如何做到，无非有四种情况：
一、 $size(l(l(t))) > size(r(t))$ ，即 $size(A) > size(R)$ ，我们操作如下：

  1. $r_rotate(t)$ ，完成后树的结构如下
    R

  2. 完成后 $t,L,A,R$ 都已满足性质，但仍可能出现 $size(C) > size(B)$ 或 $size(D) > size(B)$ ，所以我们还需调用 $maintain(t)$ ，完成后 $t$ 所在子树满足了性质

  3. 此时 $L$ 的右子树可能已经被改变形状，不满足性质，所以必须再次 $maintain(t)$

二、 $size(r(l(t))) > size(r(t))$ ，即 $size(B) > size(R)$ ，此时情况较为复杂，需要考虑 $B$ 的子树：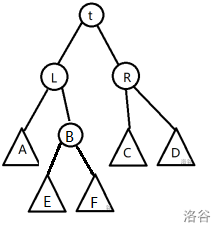
SBT_2

  1. $l_rotate(t)$ ，完成后树的结构如下:
    L

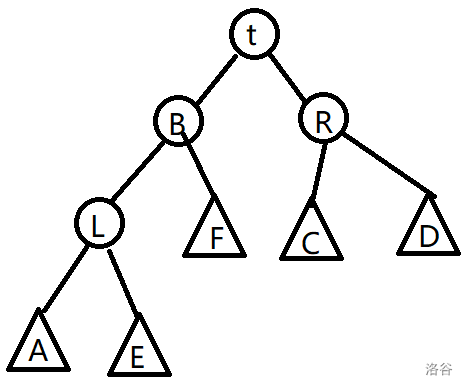
  2. 然后 $r_rotate(t)$ ，完成后树的结构如下：
    L_R

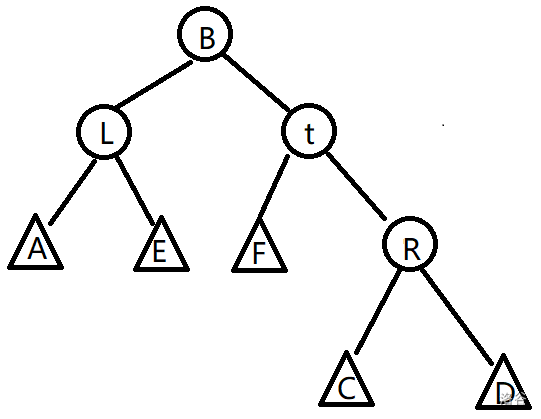
  3. 在两次旋转后，满足性质的有 $A,E,F,R$ ，我们调用 $maintain(L)$ 和 $maintain(t)$ 来修复 $B$ 的儿子

  4. 现在， $B$ 的儿子都是满足性质的了，只需再调用一次 $maintain(B)$

三、 $size(r(r(t))) > size(l(t))$ ，即 $size(D) > size(L)$ ，与情况一相反

四、 $size(r(r(t))) > size(l(t))$ ，即 $size(D) > size(L)$ ，与情况二相反

综上所述，我们可以写出伪代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
miantain(t){
    if(size(l(l(t)))>size(r(t))){
        r_rotate(t)
        miantain(r(t))
        miantain(t)
    }
    if(size(r(l(t)))>size(r(t))){
        l_rotate(l(t))
        r_rotate(t)
        miantain(l(t))
        miantain(r(t))
        miantain(t)
    }
    if(size(r(r(t)))>size(l(t))){
        l_rotate(t)
        miantain(l(t))
        miantain(t)
    }
    if(size(l(r(t)))>size(l(t))){
        r_rotate(r(t))
        l_rotate(t)
        miantain(l(t))
        miantain(r(t))
        miantain(t)
    }
}

这段代码有点复杂，在通常情况下，一棵树只会出现情况一、情况二或情况三、情况四，我们不妨多传一个 $bool$ 来简化代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
void maintain(int &t,bool flag){
    if(!flag){
        if(size(l(l(t)))>size(r(t))) r_rotate(t);
        else if(size(r(l(t)))>size(r(t))){
            l_rotate(l(t));
            r_rotate(t);
        }
        else return ;
    }
    else{
        if(size(r(r(t)))>size(l(t))) l_rotate(t);
        else if(size(l(r(t)))>size(l(t))){
            r_rotate(r(t));
            l_rotate(t);
        }
        else return ;
    }
    maintain(l(t),false);
    maintain(r(t),true);
    maintain(t,true);
    maintain(t,false);
}

至此我们还有两个问题：为啥 $maintain(l(t),true),maintain(r(t),false)$ 被省略了？而 $maintain(t)$ 的时间复杂度又是多少呢？下面我们来讨论。

首先是为何省略：
在情况一的图中（即右旋后的图），因为插入后 $size(A)>size(R)$ 所以 $size(B)$ 一定仍和插入前一样，即仍有 $size(B)\le size(R)$ ，故 $B$ 的子节点大小一定小于 $R$ ，即根本不需要 $maintain(r(t),false)$ 。其余情况同理。

然后我们来分析时间复杂度：
我们设 $SD$ 表示所有节点的深度和，明显， $SD$ 越小，BST（二叉搜索树）越优，并设 $T$ 表示 $maintain$ 中的旋转次数。
回顾整个 $maintain$ 我们发现在每次旋转后 $SD$ 总是在减小（不妨设减小了 $r$ ），所以，一个高度为 $O(\log{n})$ 的树，其深度和 $SD$ 总是保持在 $O(n\log{n})$ ，而在插入 $SD$ 仅增加 $O(log{n})$ ，故有： $SD=n \times O(\log{n})-T \times r=O(\log{n})$ ,取 $r$ 最小为 $1$ ，则 $T=O(\log{n})$ 。
于是，得到 $maintian$ 的平摊时间是：
$\frac{O(T)+O(n\log{n})+O(T)}{n\log{n}}=O(1) $

操作

SBT的基本操作如下： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
void insert(int &t,int v){ //插入
    if(!t){
        t=++cnt;
        tr[t].inint(v);
    }
    else{
        ++size(t);
        if(v<=v(t)) insert(l(t),v);
        else insert(r(t),v);
        maintain(t,v>v(t));
    }
}
int del(int &t,int v){ //删除,返回被删的值
    int ret=0;
    --size(t);
    if((v==v(t))||((v<v(t))&&!l(t))||((v>v(t))&&!r(t))){ //若找到或无法继续找
        ret=v(t);
        if(!l(t)||!r(t)) t=l(t)+r(t); //若只有一个儿子(或没有),就让儿子代替自己的位置
        else v(t)=del(l(t),v(t)+1); //否则就把左子树中最大的数移动到自己的位置
        return ret;
    }
    else{
        if(v<v(t)) return del(l(t),v);
        else return del(r(t),v);
    }
    // 一个优化？
    // maintain(t,false);
    // maintain(t,true);
}
bool find(int &t,int v){ //查找关键字为v的节点
    if(!t) return false;
    if(v<v(t)) return find(l(t),v);
    else return (v(t)==v||find(r(t),v)); 
}
int get_rank(int &t,int v){ //返回v在以t为根的树中的排名
    if(!t) return 1;
    if(v<=v(t)) return get_rank(l(t),v);
    else return size(l(t))+1+get_rank(r(t),v);
}
int select(int &t,int k){ //返回以t为根的树中排名第k的值
    if(k==size(l(t))+1) return v(t);
    if(k<=size(l(t))) return select(l(t),k);
    else return select(r(t),k-1-size(l(t)));
}
int pred(int &t,int v){ //返回比v小的最大的数
    int ret;
    if(!t) return v;
    if(v<=v(t)) return pred(l(t),v);
    else{
        ret=pred(r(t),v);
        if(ret==v) ret=v(t);
        return ret;
    }
}
int succ(int &t,int v){ //返回比v大的最小的数
    int ret;
    if(!t) return v;
    if(v(t)<=v) return succ(r(t),v);
    else{
        ret=succ(l(t),v);
        if(ret==v) ret=v(t);
        return ret;
    }
}

注：

  1. 在 $insert$ 操作中，如果插入了两个值相同的节点，BST并不会像Splay一样用一个 $cnt$ 来记录，而是直接新建节点，把两个相同的值放在两个不同的节点上

  2. 在 $del$ 操作中，有一个小优化，即注释掉 $miantain$ ，在删除后不去维护SBT的结构（但性质是一定满足了的）,这样做树的高度变成了 $O(\log{K})$ ，这里 $K$ 表示插入的节点个数

时间分析

我们来分析SBT的时间复杂度（其实不用分析了，是个人都知道是 $O(log{n})$）:
设 $f[h]$ 表示高度为 $h$ 的SBT包含的最少节点数，有：
$$
f[h]=\begin{cases}
1 & (h=0)\
2 & (h=1)\
f[h-1]+f[h-2]+1 & (h>1)
\end{cases}
$$

证明如下：
我们把一个高度为 $h-1$ 的SBT作为当前高度为 $h$ 的SBT的左子树，目前有 $f[h-1]+1$ 个节点，但为了满足SBT性质，右子树至少应有 $f[h-2]$ 个节点。
然后，我们可以由 $fibonacci$ 数列得到 $f[h]$ 计算公式：
$$f[h]=\sum_{i=0}^{h} Fibonacci[i]=\left | \frac{\alpha^{h+3}}{\sqrt{5}} \right |$$
其中 $\alpha=\frac{1+\sqrt{5}}{2}$

设 $maxh$ 表示有 n 个节点的SBT的最坏高度，有
$$f[maxh]=\left | \frac{\alpha^{h+3}}{\sqrt{5}} \right |-1 \le n \Rightarrow$$
$$\frac{\alpha^{h+3}}{\sqrt{5}} \le n+1.5 \Rightarrow$$
$$maxh \le \log_{\alpha}{\sqrt{5}(n+1.5)}-3 \Rightarrow$$
$$maxh \le 1.44\log_{2}{n+1.5}-1.33$$
明显，SBT高度为 $O(\log{n})$。
且SBT效率一般优于其他平衡树。

代码

P6136

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
#include<bits/stdc++.h>
using namespace std;
const int N=2e6+5;
int n,m,last=0,ans=0;
struct SBT{
    int v;
    int size;
    int l,r;
    void inint(int _v){
        v=_v;
        size=1;
        l=r=0;
    }
#define v(i) tr[i].v
#define size(i) tr[i].size
#define l(i) tr[i].l
#define r(i) tr[i].r
}tr[N];
int cnt=0,root=0;
/*-----------------------------SBT--------------------------*/
void r_rotate(int &t){
    int k=l(t);
    l(t)=r(k);
    r(k)=t;
    size(k)=size(t);
    size(t)=size(l(t))+size(r(t))+1;
    t=k;
}
void l_rotate(int &t){
    int k=r(t);
    r(t)=l(k);
    l(k)=t;
    size(k)=size(t);
    size(t)=size(l(t))+size(r(t))+1;
    t=k;
}
void maintain(int &t,bool flag){
    if(!flag){
        if(size(l(l(t)))>size(r(t))) r_rotate(t);
        else if(size(r(l(t)))>size(r(t))){
            l_rotate(l(t));
            r_rotate(t);
        }
        else return ;
    }
    else{
        if(size(r(r(t)))>size(l(t))) l_rotate(t);
        else if(size(l(r(t)))>size(l(t))){
            r_rotate(r(t));
            l_rotate(t);
        }
        else return ;
    }
    maintain(l(t),false);
    maintain(r(t),true);
    maintain(t,true);
    maintain(t,false);
}
void insert(int &t,int v){
    if(!t){
        t=++cnt;
        tr[t].inint(v);
    }
    else{
        ++size(t);
        if(v<=v(t)) insert(l(t),v);
        else insert(r(t),v);
        maintain(t,v>v(t));
    }
}
int del(int &t,int v){
    int ret=0;
    --size(t);
    if((v==v(t))||((v<v(t))&&!l(t))||((v>v(t))&&!r(t))){
        ret=v(t);
        if(!l(t)||!r(t)) t=l(t)+r(t);
        else v(t)=del(l(t),v(t)+1);
        return ret;
    }
    else{
        if(v<v(t)) return del(l(t),v);
        else return del(r(t),v);
    }
}
bool find(int &t,int v){
    if(!t) return false;
    if(v<v(t)) return find(l(t),v);
    else return (v(t)==v||find(r(t),v)); 
}
int get_rank(int &t,int v){
    if(!t) return 1;
    if(v<=v(t)) return get_rank(l(t),v);
    else return size(l(t))+1+get_rank(r(t),v);
}
int select(int &t,int k){
    if(k==size(l(t))+1) return v(t);
    if(k<=size(l(t))) return select(l(t),k);
    else return select(r(t),k-1-size(l(t)));
}
int pred(int &t,int v){
    int ret;
    if(!t) return v;
    if(v<=v(t)) return pred(l(t),v);
    else{
        ret=pred(r(t),v);
        if(ret==v) ret=v(t);
        return ret;
    }
}
int succ(int &t,int v){
    int ret;
    if(!t) return v;
    if(v(t)<=v) return succ(r(t),v);
    else{
        ret=succ(l(t),v);
        if(ret==v) ret=v(t);
        return ret;
    }
}
int main(){
    scanf("%d%d",&n,&m);
    int a;
    for(int i=1;i<=n;++i){
        scanf("%d",&a);
        insert(root,a);
    }
    while(m--){
        int op,x;
        scanf("%d%d",&op,&x);
        x^=last;
        if(op==1){
            insert(root,x);
        }
        else if(op==2){
            del(root,x);
        }
        else if(op==3){
            last=get_rank(root,x);
            ans^=last;
        }
        else if(op==4){
            last=select(root,x);
            ans^=last;
        }
        else if(op==5){
            last=pred(root,x);
            ans^=last;
        }
        else{
            last=succ(root,x);
            ans^=last;
        }
    }
    printf("%d\n",ans);
    return 0;
}