Dyd's Blog

He who has a strong enough why can bear almost any how.

背包问题

Posted on Edited on In
Symbols count in article: 2.6k Reading time ≈ 2 mins.

只写了一点点

回顾

01背包

1
2
3
4
5
6
7
8
9
memset(f,0xcf,sizeof f);
ans=-INF;

for(int i=1;i<=n;++i)
	for(int j=m;j>=v[i];--j)
  		f[j]=max(f[j-v[i]]+w[i],f[j]);

for(int i=1;i<=m;++i)
	ans=max(ans,f[i]);

完全背包

1
2
3
4
5
6
7
8
9
memset(f,0xcf,sizeof f);
ans=-INF;

for(int i=1;i<=n;++i)
	for(int j=v[i];j<=m;++j)
  		f[j]=max(f[j-v[i]]+w[i],f[j]);

for(int i=1;i<=m;++i)
	ans=max(ans,f[i]);

多重背包

用二进制优化转换为01背包

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void split(Node x){
    int p=1;
    while(x.p>=p){
        b[++o].c=x.c*p;
        b[o].t=x.t*p;
        b[o].p=1;
        x.p-=p;
        p<<=1;
    }
    if(x.p){
        b[++o].c=x.c*x.p;
        b[o].t=x.t*x.p;
        b[o].p=1;
    }
}

新知

单调队列优化的多重背包

引入

我们考虑多重背包的转移方程（二维），思考，能否像完全背包一样，让 $f[i][j]=max(f[i-1][j],f[i][j-v]+w)$ ，以此来优化呢？
观察：
对比
我们会发现和完全背包相同的是，红色方框内的两个表达式一一对应，相差一个 $w$ ，但是， $f[i][j-v]$ ，有一项没有对应上。
这是为何呢？原因很简单，完全背包 $f[i][j]$ 在不考虑越界的情况下有无穷多种转移情况，在去掉最前端的 $f[i-1][j]$ 后还有无穷多种，恰好可以与 $f[i][j-v]$ 的无穷多种情况一一对应。
但是，变成多重背包后， $f[i][j]$ 只有 $s$ 种，即有限种转移情况，在去掉最前端的 $f[i-1][j]$ 后只有 $s-1$ 种，与 $f[i][j-v]$ 的 $s$ 种一一对应后，还剩一个。
但就是这多余的一个，导致我们无法用 $f[i][j]=max(f[i-1][j],f[i][j-v]+w)$ 来转移，因为多余的一个情况无法预料。

但这仍可以给我们一些启示：
在数轴上标出 $x=j+kv,k \in \mathbb{Z}$ ，即， $x \equiv j \pmod v$ 。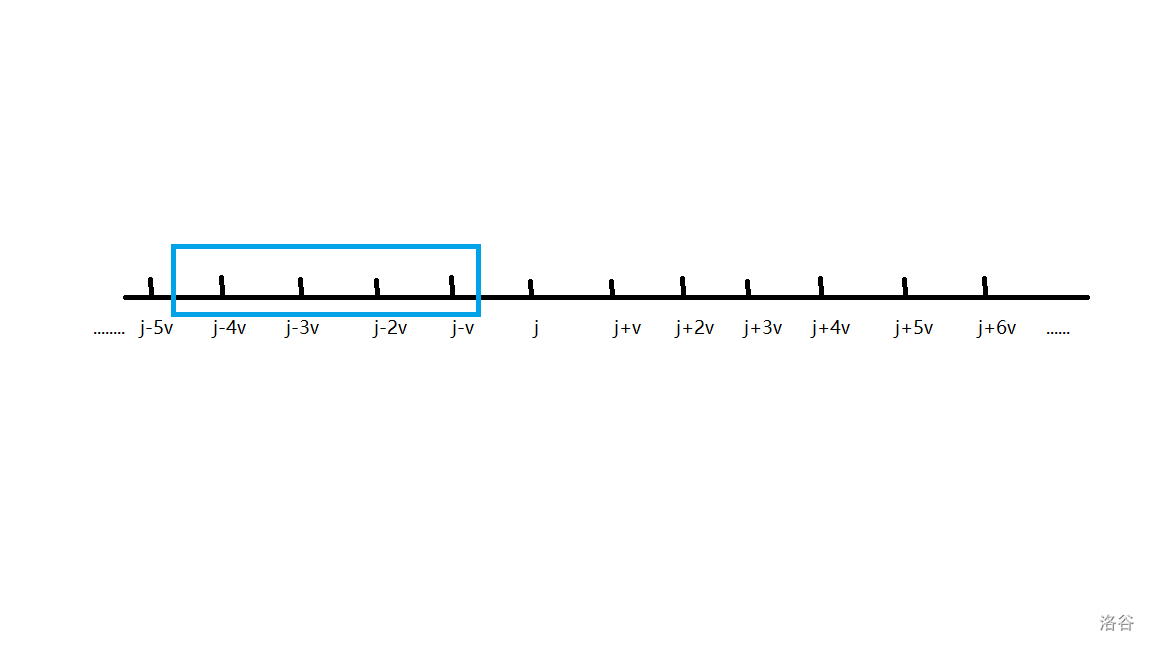
滑动
$j$ 是由它前面 $s$ 个点的最大值
转移过来的，即蓝色窗口中标出的点的最大值，而 $j-v$ 也是由其前方 $s$ 个点的最大值转移而来，也就是说，窗口大小不变，窗口在数轴上滑动。
需要注意的是，数轴是无限的，但数组的转移是有边界的，所以我们可以把数轴上无意义的点设为负无穷（当然具体视情况而定） ，这样防止越界。
在解决了以上问题后，我们就只需要找出一种快速求滑动窗口最值的方法即可，而以前学过的单调队列可以在线性的时间内维护该问题。

具体来说，我们把“倒序循环 $j$ ”，改为对每个余数 $u \in [0,v_i-1]$ 倒序循环 $p=\left \lfloor (m-u)/v_i \right \rfloor \sim 0$ ，对应的状态就是 $j=u+p * v_i$ ，由于只能选 $c_i$ 个，故状态转移方程为：
$$f[u+p * v_i]=\max_{p-c_i \le k \le p-1} (f[u+k * v_i]+(p-k) * w_i)$$
我们发现，把 $i,u$ 看做定值，当内层变量 $p$ 减少 $1$ 时，决策 $k$ 的取值范围 $[p-c_i,p-1]$ 均单调减小，所以我们可以维护一个决策点 $k$ 单调递减，数值 $f[u+k * v_i]-k * w_i$ 递减的队列。

例题

多重背包问题

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include <bits/stdc++.h>
using namespace std;
const int N=100000+5;
int n,m,ans=0;
int f[N],v[N],w[N],c[N],q[N];
int calc(int i,int u,int k){
	return f[u+k*v[i]]-k*w[i];
}
int main(){
	scanf("%d%d",&n,&m);
	memset(f,0xcf,sizeof f);
	f[0]=0;
	for(int i=1;i<=n;++i){
		scanf("%d%d%d",&v[i],&w[i],&c[i]);
		for(int u=0;u<v[i];++u){ //u:余数 
			int hh=1,tt=0;
			int maxp=(m-u)/v[i];
			//将初始的候选集合插入队列 
			for(int k=maxp-1;k>=max(maxp-c[i],0);--k){ 
				while(hh<=tt&&calc(i,u,q[tt])<=calc(i,u,k)) --tt;
				q[++tt]=k; 
			}
			//dp 
			for(int p=maxp;p>=0;p--){ //循环状态 
				//排除过时决策
				while(hh<=tt&&q[hh]>p-1) ++hh;
				//取队头转移
				if(hh<=tt) 
					f[u+p*v[i]]=max(f[u+p*v[i]],calc(i,u,q[hh])+p*w[i]);
				//新决策入队,同时维护单调
				if(p-c[i]-1>=0){
					while(hh<=tt&&calc(i,u,q[tt])<=calc(i,u,p-c[i]-1)) --tt;
					q[++tt]=p-c[i]-1;
				} 
			} 
		}
	}
	for(int i=1;i<=m;++i) ans=max(ans,f[i]);
	printf("%d",ans);
    return 0;
}