Dyd's Blog

He who has a strong enough why can bear almost any how.

网络流

Posted on Edited on In
Symbols count in article: 21k Reading time ≈ 19 mins.

老有用了

网络流

网络流的基本概念

一个有向图 $G=(V,E)$ ，每条有向边 $(x,y)$ 都有一个给定的容量记为 $c(x,y)$ （若不存在边 $(x,y)$ ，则 $c(x,y)=0$ ），图中还有两个特殊节点源点、汇点分别记为 $S$ 、 $T$ ； $S$ 会源源不断地流出无穷的水流，但每条边只能通过 $c(x,y)$ 的水流， $T$ 可以容纳无穷的水流，而其余个点无法容纳水流（即流入就必须全部流出）

任意一种满足条件的流水方法（即让水流从 $S$ 流到 $T$ ）叫做流函数，记为 $f(x,y)$ （表示从点 $x$ 流向 $y$ 的水流），明显，流函数具有如下性质：

  • $0 \le f(x,y) \le c(x,y)$

  • $f(x,y)=-f(y,x)$ （即从 $x$ 流向 $y$ 的流量也就是从 $y$ 流向 $x$ 的流量的相反数）

  • $\forall x \ne S,T, \sum\limits_{u,x\in E}^{}f(u,x)= \sum\limits_{x,v\in E}^{}f(x,v)$ （即除 $S$ ， $T$ 外其余点流入流量等于流出流量，流量守恒）

残量网络

对于任意合法的流函数 $f$ ，都可构建一个新图 $G2$ （其实应该记做 $G’$ 但这里为了方便记为 $G2$ ），构建方法如下：

  1. 将原图每条边容量变为 $c(x,y)-f(x,y)$ （即减掉已经用掉的流量）
  2. 对于每条边 $(x,y)$ ，创建它的反向边 $(y,x)$ 并令 $c(y,x)=f(x,y)$ （即以流的流量让它可以反悔再流回来）

该图G2被我们叫做残量网络

需要注意的是,反向边是我们新加的,原图中并不存在,若原图中本就有边 $(x,y)$ 和边 $(y,x)$ （即原图就有反向边），应在构建原图 $G$ 时就新建一点 $z$ ，使得 $(y,x)$ 变为 $(y,z)$ ， $(z,x)$ 。

如图（画的丑求你憋着吧！）
输入
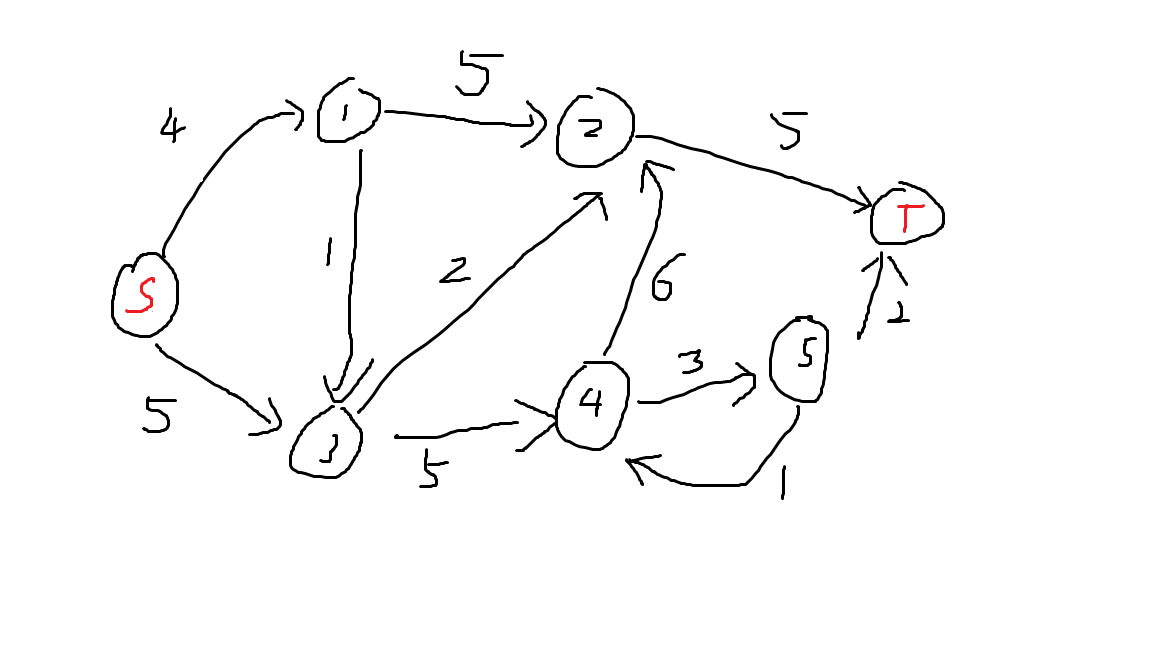
$\uparrow$ 这是输入的有向图。
G
$\uparrow$ 这是去掉反向边的原图 $G$ 。
f
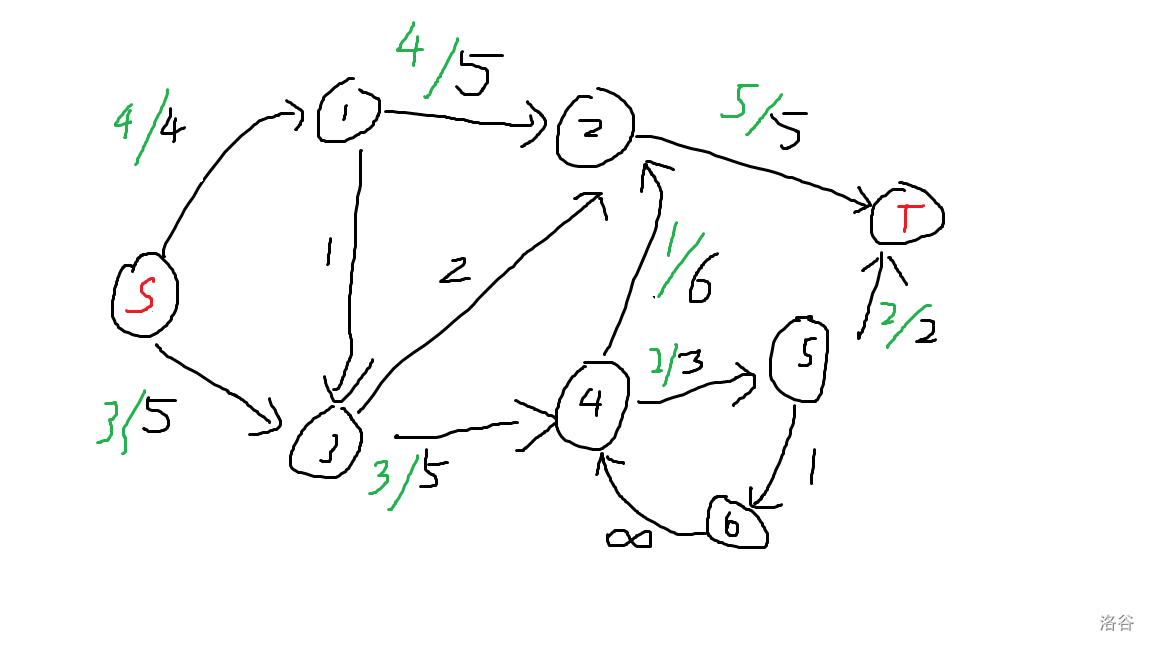
$\uparrow$ 这是一个合法的流函数，图中绿色代表 $f(x,y)$ 。
G2
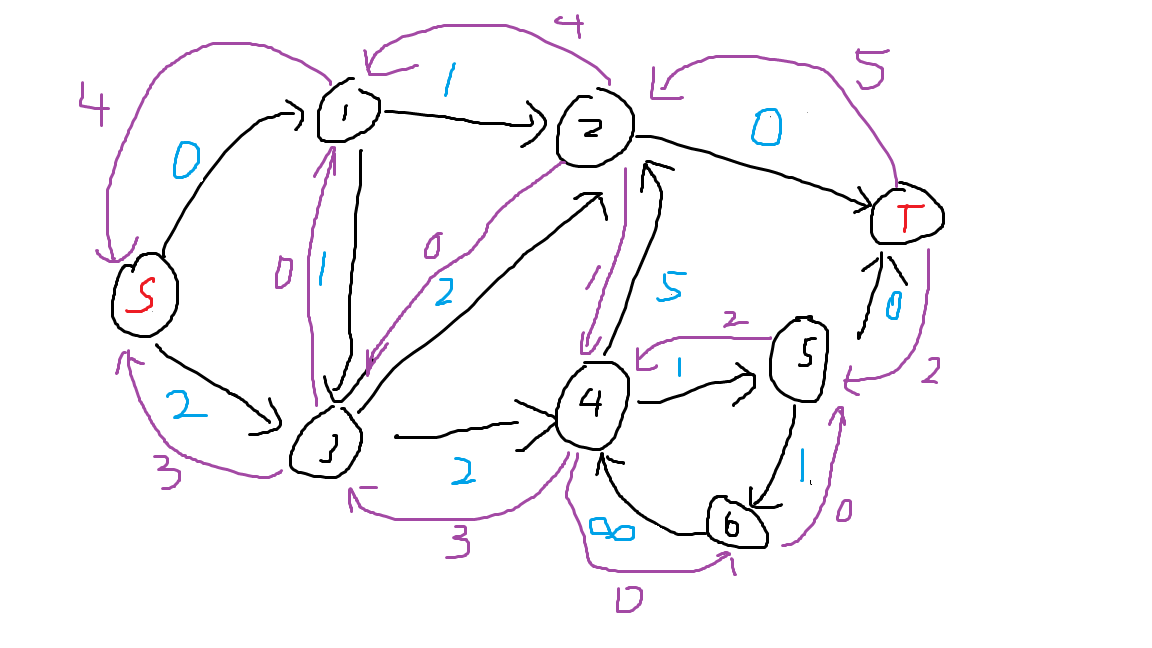
$\uparrow$ 这是该流函数的残量网络，蓝色为原图边容量（已改变)，紫色为加入的反向边。

最大流

给定一个网络 $G$ ,对于所有合法的 $f$ ,从 $S$ 流出的流量最大的记为该网络的最大流，如上图中最大流为 $7$ （即是绿色的流函数）

最大流的求法很多,但基本思路大体相同：

  1. 先找到任意的一个流函数 $f$ ，并构建它的残量网络 $G2$

  2. 在 $G2$ 中寻找 $G2$ 的合法流函数（我们一般记其为 $f’$ ，文中称其为 $f2$ ， $f2$ 也叫做增广路）

  3. 将找到的增广路加上原图的流函数构成新的流函（即 $f_{now}=f+f2$ 并将 $G2$ 更新成为 $f_{now}$ 的残量网络）

  4. 重复第 $2$ ， $3$ 步直到无增广路，此时的 $f$ 即是最大流

该思路的证明比较简单，想了解的可以自己百度，下面放两种算法（都已通过P3376）：

一.Edmonds-Karp(EK算法)

该算法就是以上思路的直接实现，（未优化版）几乎不会用，仅了解即可，另外，由于这是我很久以前的代码，码风不太好

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
//Edmonds-Karp    O(nm^2)
//n+m = 10^3~10^4
#include<iostream>
#include<cmath>
#include<cstring>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
using namespace std;
const int N=1000+5,M=20000+5;
const int INF=0x3f3f3f3f;
int n,m,S,T;	
int q[N],incf[N],pre[N];		//q队列,incf残留网络流量,pre前驱边 
bool vis[N]; 
int h[N],e[M],f[M],ne[M],idx=0;		//e目标编号,f该边流量	
void add(int x,int y,int c){		//使用成对储存的技巧i^1及是i的反向边,不懂的请看第二大部分
	e[idx]=y,f[idx]=c;
	ne[idx]=h[x],h[x]=idx++;
	
	e[idx]=x,f[idx]=0;
	ne[idx]=h[y],h[y]=idx++;
	return ;
}
bool bfs(){			//寻找增广路 
	int hh=0,tt=0;
	memset(vis,false,sizeof vis);
	q[0]=S,vis[S]=true,incf[S]=INF;		//初始化,把S的出流量定为无穷大 
	while(hh<=tt){
		int t=q[hh++];
		for(int i=h[t];i!=-1;i=ne[i]){
			int ver=e[i];
			if(!vis[ver]&&f[i]){		//未到过且还有流量 
				vis[ver]=true;
				incf[ver]=min(incf[t],f[i]);	//最大流量为各边流量最小值 
				pre[ver]=i;					//记录前驱边 
				if(ver==T) return true;		
				q[++tt]=ver;
			}
		}
	}
	return false;
}
long long EK(){
	long long maxflow=0;		//这里仅是本人习惯开了long long
	while(bfs()){		//若存在增广路 
		maxflow+=incf[T];		 
		for(int i=T;i!=S;i=e[pre[i]^1]){	//pre[i]为前驱边->pre[i]^1为前驱边的反向边 
                                                        //->e[pre[i]^]为该反向边的目标点,即是前一个点
			//更改残留网络								 
			f[pre[i]]-=incf[T];
			f[pre[i]^1]+=incf[T];
		}
	}
	return maxflow;
}
int main(){
	scanf("%d%d%d%d",&n,&m,&S,&T);
	memset(h,-1,sizeof h);
	for(int i=1;i<=m;++i){
		int x,y,c;
		scanf("%d%d%d",&x,&y,&c);
		add(x,y,c);
	}	
	printf("%ld",EK());
	return 0;
}

二.Dinic算法

通过构建分层图来使增广时一次性增广多条增广路,是以上思路的优化,本人较为偏爱该算法（这是以前的码风，由于注释很多，我懒得再打一遍，所以保留）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
//Dinic   O(n^2m)
//n+m = 10^4~10^5
#include<iostream>
#include<cmath>
#include<cstring>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
using namespace std;
typedef long long ll; 
const ll N=1000+5,M=20000+5;		//有方向边M要开2倍 
const ll INF=0x3f3f3f3f;
ll n,m,S,T;	
ll q[N],d[N],cur[N];		//q队列,d高度,cur当前弧优化 
ll h[N],e[M],f[M],ne[M],idx=0;		//h,e,ne,idx邻接表,f流量 
void add(ll x,ll y,ll c){		 
	e[idx]=y,f[idx]=c;
	ne[idx]=h[x],h[x]=idx++;
	
	e[idx]=x,f[idx]=0;
	ne[idx]=h[y],h[y]=idx++;
	return ; 
}
bool bfs(){			//寻找有无增广路并建立分层图 
	ll hh=0,tt=0;
	memset(d,-1,sizeof d);
	q[0]=S,d[S]=0,cur[S]=h[S];	 //S初始高度为0,当前弧初始为第一条出边 
	while(hh<=tt){
		ll t=q[hh++];
		for(ll i=h[t];i!=-1;i=ne[i]){
			ll ver=e[i];
			if(d[ver]==-1 &&f[i]){		//一定要判断容量大于0 
				d[ver]=d[t]+1;		//层数 
				cur[ver]=h[ver];	//当前弧初始为第一条出边 		
				if(ver==T) return true;		
				q[++tt]=ver;
			}
		}
	}
	return false;
}
ll find(ll u,ll limit){	//找到增广路,find(u,limit)表示从点u开始,
									//从S到u的最大容量为limit 
	if(u==T) return limit;
	ll flow=0;		//flow表示从u向T流的最大流量 
	for(ll i=cur[u];i!=-1&&flow<limit;i=ne[i]){		//从未满的路径开始搜
														//flow<limit是很重要的优化! 
		cur[u]=i;		//当前弧优化,搜到i就意味着i前的边已用完,将当前弧更新 
		ll ver=e[i];
		if(d[ver]==d[u]+1&&f[i]){		//保证当前点在上一点的下一层,同样要注意f>0 
			ll t=find(ver,min(f[i],limit-flow));	
			if(!t) d[ver]=-1;		//若t到终点无增广路径,就删去点ver(把ver高度定为-1) 
			
			f[i]-=t;
			f[i^1]+=t;
			flow+=t; 
		} 
	}
	return flow;
}
ll Dinic(){
	ll maxflow=0,flow;	
	while(bfs())		//若存在增广路 
		while(flow=find(S,INF)) 		//找出当前图上所有增广路 
			maxflow+=flow;		
	return maxflow;
}
int main(){
	scanf("%lld%lld%lld%lld",&n,&m,&S,&T);
	memset(h,-1,sizeof h);
	for(int i=1;i<=m;++i){
		ll x,y,c;
		scanf("%lld%lld%lld",&x,&y,&c);
		add(x,y,c);
	}	
	printf("%lld",Dinic());
	return 0;
}

这里有一个现在码风的（ $2022/2/24$ ）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include <bits/stdc++.h>
#define STC static
using LL = long long;
const int N = 10000 + 5, M = 1e5 + 5, INF = 0x3f3f3f3f;
struct Edge{ int ne, ver, w; } e[M << 2];
int n, m, S, T;
int h[N], cur[N], idx = 0, dep[N];
void add(int x, int y, int z){ e[idx] = {h[x], y, z}, h[x] = idx++; }
void dad(int x, int y, int z){ add(x, y, z), add(y, x, 0); }
bool dfs()
{
    STC int q[N];
    int hh = 1, tt = 1, x, y;
    for (memset(dep, 0, sizeof dep), q[dep[S] = 1] = S, cur[S] = h[S]; hh <= tt; )
        for (int i = h[x = q[hh++]]; i != -1; i = e[i].ne) if (!dep[y = e[i].ver] && e[i].w)
		{
			dep[y] = dep[x] + 1, cur[y] = h[y];
			if (y == T) return true;
			q[++tt] = y;
		}
    return false;
}
int find(int x, int lim)
{
    if (x == T) return lim;
    int flow = 0, y, t;
    for (int i = cur[x]; i != -1 && flow < lim;  i = e[i].ne)
    {
        cur[x] = i; //这里非常玄学,一定要这样写,压行的话可能会TLE
        if (dep[y = e[i].ver] == dep[x] + 1 && e[i].w)
        {
            if (!(t = find(y, std::min(lim - flow, e[i].w)))) dep[y] = 0;
            e[i].w -= t, e[i ^ 1].w += t, flow += t;
        }
    }
    return flow;
}
LL dinic()
{
    LL res = 0, flow;
    while (dfs()) while(flow = find(S, INF)) res += flow;
    return res;
}
int main()
{
    scanf("%d %d %d %d", &n, &m, &S, &T);
    memset(h, -1, sizeof h);
    for (int a, b, c; m--; dad(a, b, c)) scanf("%d %d %d", &a, &b, &c);
    printf("%lld\n", dinic());
    return 0;
}

无源汇上下界可行流

在这类问题中不在仅存在容量上界 $c$ ，还存在下界（不妨记为 $l$ ），并且不存在 $S$ ， $T$ 两点

对于此类问题，我们可以用如下操作变为网络最大流：

  1. 新建源点和汇点

  2. 为满足性质1（忘了的上去看），将 $c$ 变为 $c-l$ ，即原来 $l(x,y) \le f(x,y) \le c(x,y)$ 变为 $0 \le f(x,y) \le c(x,y)-l(x,y)$

  3. 经过第2步后我们发现流量不守恒，故用一个数组 $ve$ （Virtual Edge）储存每个点的流量变化量，即对于边 $(x,y)$ ，经第2步变化后， $x$ 的出流量少了 $l(x,y)$ ， $y$ 的入流量少了 $l(x,y)$ ，故 $ve(x)-=l(x,y)$ ， $ve(y)+=l(x,y)$

  4. 利用第3步统计的 $ve$ 数组，新建虚拟边使流量守恒，即若 $ve(x)>0$ ，新建边 $(S,x)$ 并令 $c(S,x)=ve(x)$ ；若 $ve(x)<0$ ，新建边 $(x,T)$ 并令 $c(x,T)=-ve(x)$ ；

  5. 跑一遍 $S$ 到 $T$ 的最大流，若 $S$ （或 $T$ ）的所有边都可以流满，就说明存在可行流

经过如上操作，就将其变为一个基本的最大流问题，我们把这样建成的图称作虚拟图（仅是本人习惯），记为 $G3$

有源汇上下界可行流

此类问题相比于上一类区别在于原题中就存在源点和汇点（为以示区别记为 $s$ 、 $t$ ）

而解决方式与上类问题类似，区别仅在于我们要将点 $s$ 、 $t$ 这两个不满足流量守恒的点变为普通点，再用新建的 $S$ 、 $T$ 当为源点

而使其变成普通点的方式即是新建一条边 $(t,s)$ 并令
$c(t,s)= \infty$ （正无穷）

有源汇上下界最大流

好，现在问题来了，我们求解可行流时就是求的 $G3$ 的最大流，那么如果我们现在要求原图 $G$ 的可行流中的最大流我们该怎么办？

仔细思考，发现我们还有一个图没用——原图的残量网络 $G2$ ！辣么，我们可否使用这三个图求出答案呢？

当然是可以的，不然我讲个屁啊，而方法如下：

  1. 同上类问题跑出 $G3$ 的最大流记为 $flow3$ ，并将此时原图中的流函数记为 $f3$
  2. 构建原图 $G$ 关于 $f3$ 的残量网络 $G2$ ，求出 $G2$ 中的曾广路，我们发现这就等价于求出 $G$ 的最大流 $flow$ （注意此时用的是原图 $G$ ，故应删去边 $(t,s)$ ）
  3. 最后答案即是 $flow+flow3$

例题

题目大意

有 $n$ 天， $m$ 位少女，至少为她们每人拍 $G(i)$ 张照片，每天总的最多拍 $D(i)$ 张，且每天只能为特定的少女拍照，张数为 $x \in [L,R]$ 。

建立模型

我们可以很轻松的由题目标题得出应使用网络流，并在稍微，指3天，思考后得出如下方法：

  • 建立原图 $G$ ：
    1. 建立源点 $s=1$ ，汇点 $t=m+n+2$ ，并将少女建为点 $2 \sim m+1$ ，天数建为点 $m+2 \sim n+m+1$
    2. 将少女至少要拍的照片数 $G(i)$ 定为下界，无穷大定为上界，让少女 $x$ 与源点 $s$ 相连，即建立边 $(s,x)$ （ $x \in [2,m+1]$ ）并使 $c(s,x)=\infty -G(i)$
    3. 将每天的最大拍照量定为上界， $0$ 为下界，让天数 $y$ 与汇点 $t$ 相连，即建边 $(y,t)$ （ $y \in [m+2,m+n+1]$ ）并使 $c(y,t)=D(i)-0$
    4. 将少女与天相连，定上下界为 $[L,R]$ ，即建边 $(x,y)$ （ $x \in [2,m+1],y \in [m+2,m+n+1]$ ）并使 $c(x,y)=R-L$
    5. 在构建原图的同时维护 $ve$ 数组
  • 构建虚拟图 $G3$ ：
    1. 建立源点 $S=0$ ， $T=n+m+3$
    2. 用 $ve$ 数组建立连接 $S$ ， $T$ 与其他点的边
    3. 增加边 $(t,s)$ ，并使 $c(t,s)=\infty$
    4. 并同时维护 $outflow$ （记录从S流出的流量,用于判定是否满流）
  • 求解 $G3$ 的最大流
    1. 直接用Dinic求解
    2. 判断 $Dinic()$ 是否等于 $outflow$ ，若不等，则说明原图无可行流（原题无解）
    3. 若相等，用 $res$ 记录此时 $s$ 到 $t$ 的流量，并进入下一步
  • 求解 $G$ 的最大流（即是 $G2$ 中的曾广路）
    1. 删去边 $(t,s)$
    2. 使 $S=s$ ， $T=t$ （即将 $G3$ 变为 $G$ ）
    3. Dinic求解最大流，答案即为 $Dinic()+res$

代码

以前的码风

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
#include<cstdio>
#include<cstring>
using namespace std;
const int N=1000000+5,M=1000000+5,INF=2147483647;
int n,m;	//如题意 
int nn,s,t,S,T;		//nn:原图中的点数,s:原图的源点,S虚拟图的源点,t,T同理 
int q[N],d[N],cur[N],ve[N];			//q:队列,d:高度,cur:当前弧优化,ve(Virtual Edge):虚拟边 
int h[N],e[N],f[N],ne[N],idx=0;			//h,e,ne,idx:邻接表,f:流量 
inline void add(int x,int y,int c){
	e[idx]=y,f[idx]=c,ne[idx]=h[x],h[x]=idx++;
	e[idx]=x,f[idx]=0,ne[idx]=h[y],h[y]=idx++;			//使用成对储存的技巧 
	return ;
}
inline int min(int a,int b){
	return a<b? a:b;
}
bool bfs(){				//寻找有无增广路并建立分层图 
	int hh=0,tt=0;
	memset(d,-1,sizeof d);
	q[hh]=S,d[S]=0,cur[S]=h[S];			//S初始高度为0,当前弧初始为第一条出边 
	while(hh<=tt){
		int p=q[hh++];
		for(int i=h[p];i!=-1;i=ne[i]){
			int ver=e[i];
			if(d[ver]==-1&&f[i]){			//一定要判断容量大于0 
				d[ver]=d[p]+1;				//层数  
				cur[ver]=h[ver];			//当前弧初始为第一条出边 
				if(ver==T) return true;
				q[++tt]=ver;
			}
		}
	}
	return false;
}
int find(int u,int limit){			//找到增广路,find(u,limit)表示从点u开始,
									//从S到u的最大容量为limit 
	if(u==T) return limit;
	int nowflow=0;					//nowflow表示从u向T流的最大流量 
	for(int i=cur[u];i!=-1&&nowflow<limit;i=ne[i]){		//从未满的路径开始搜
														//nowflow<limit是很重要的优化! 
		cur[u]=i;			//当前弧优化,搜到i就意味着i前的边已用完,将当前弧更新 
		int ver=e[i];
		if(d[ver]==d[u]+1&&f[i]){				//保证当前点在上一点的下一层,同样要注意f>0 
			int tflow=find(ver,min(f[i],limit-nowflow));
			if(!tflow) d[ver]=-1;				//若t到终点无增广路径,就删去点ver(把ver高度定为-1) 
			f[i]-=tflow,f[i^1]+=tflow,nowflow+=tflow;
		}
	}
	return nowflow;
}
int Dinic(){
	int maxflow=0,inflow;
	while(bfs())				//若存在增广路 
		while(inflow=find(S,INF))  maxflow+=inflow;			//找出当前图上所有增广路 
	return maxflow;
}
int main(){
	while(~scanf("%d%d",&n,&m)){
		memset(h,-1,sizeof h);
		memset(ve,0,sizeof ve);
		//构建原图 
		s=1,t=n+m+2;		//原图中s=1为源点,t=n+m+2为汇点 
		nn=n+m+2;			//nn:原图的点数 
		for(int i=2;i<=m+1;++i){	//将少女编号为2~m+1,并和源点连通 
			int G;
			scanf("%d",&G);
			add(s,i,INF-G);	
			ve[i]+=G;
			ve[s]-=G;
		}
		for(int i=m+2;i<=m+n+1;++i){	//将天数编号为m+2~m+n+1,并和汇点连通 
			int C,D;
			scanf("%d%d",&C,&D);
			add(i,t,D);
			for(int j=1;j<=C;++j){		//将天与少女连通 
				int TT,L,R;		//TT即为题中的T
				scanf("%d%d%d",&TT,&L,&R);
				TT+=2;		//注意输入中的少女是从0编号的
				add(TT,i,R-L);	
				ve[TT]-=L;			//一定要减L,别减R！ 
				ve[i]+=L; 
			}
		}
		//构建虚拟图 
		S=0,T=n+m+3;		//S=0为虚拟图源点,T=n+m+3为虚拟图汇点 
		int outflow=0;		//记录从虚拟源点出流量,用于判断是否是满流 
		for(int i=1;i<=nn;++i){		//创建虚拟边保证虚拟图中流量守恒 
			if(ve[i]>0){
				add(S,i,ve[i]);
				outflow+=ve[i]; 
			} 
			else if(ve[i]<0) add(i,T,-ve[i]);
		}
		add(t,s,INF);		//增加一条从t到s的边,保证流量守恒 
		if(Dinic()<outflow) printf("-1\n\n");		//务必两个\n 
		else{
			int res=f[idx-1];		//最后加的边的反向边的流量
									//即是当前(虚拟图的)满流中s->t的流量
			f[idx-1]=f[idx-2]=0;	//删除该边	
			S=s,T=t;		//因为现在求的是s->t的最大流量,
							//所以重新初始化源点和汇点 
			printf("%d\n\n",res+Dinic()); 		//ans即为虚拟图中s->t的流量+
												//新增加的可行流量 
		}
	}
	return 0;
}

费用流

我们已经解决了网络最大流的问题，但是，如果边不仅有容量限制，还有“价格”，也就是说，流单位容量的流还要付出一定代价该怎么办呢？

最小费用最大流(mcmf)简称费用流就可以解决这样一个问题：给定一张网络，有源点和汇点，网络上的每条边 $(u,v)$ 都有一个流量限制 $w(u,v)$ 和单位流量的费用 $c(u,v)$ ，在满足流量守恒的前提下，求出使流量最大的最小费用

其实非常简单，考虑我们Dinic的过程，其实就是不断一个寻找增广路的过程，那么我们在每次寻找增广路的时候，贪心的寻找单位费用最小的增广路，正确性显然，考虑具体实现，只需将每条边 $(u,v)$ 的反向边的费用定为 $-c(u,v)$ ，每次寻找增广路的bfs换成一个最短路即可

spfa实现

使用spfa可以简单，高效（前提是spfa没死）的实现费用流，但需要注意的是，费用流的时间复杂度是 $O(nmf)$ ，其中 $f$ 代表最大流量，这个复杂度是伪多项式的，因为 $f_{max}=2^{\frac{n}{2}},m_{max}=n^2$ ，所以最坏为 $O(n^32^{\frac{n}{2}})$ ，当然实际上远远达不到这个上界

这里用Dinic+spfa实现了一个费用流：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
#include <bits/stdc++.h>
#define STC static
using LL = long long;
const int N = 5000 + 5, M = 5e4 + 5, INF = 0x3f3f3f3f;
struct Edge{ int ne, ver, w, c; } e[M << 1];
int n, m, S, T;
int h[N], cur[N], idx = 0, dis[N];
bool vis[N];
LL maxflow, mincost;
void add(int x, int y, int z, int c){ e[idx] = {h[x], y, z, c}, h[x] = idx++; }
void dad(int x, int y, int z, int c){ add(x, y, z, c), add(y, x, 0, -c); }
bool spfa()
{
    for (int i = 1; i <= n; ++i) dis[i] = INF, cur[i] = h[i];
    std::queue<int> q; //这里只能stl,因为spfa一个点可能入队多次,空间大小未知
    int x, y;
    for (dis[S] = 0, q.push(S), vis[S] = true; !q.empty(); )
    {
        vis[x = q.front()] = false, q.pop();
        for (int i = h[x]; i != -1; i = e[i].ne) if (dis[y = e[i].ver] > dis[x] + e[i].c && e[i].w)
        {
            dis[y] = dis[x] + e[i].c;
            if (!vis[y]) vis[y] = true, q.push(y);
        }
    }
    return dis[T] != INF;
}
int find(int x, int lim)
{
    if (x == T) return lim;
    vis[x] = true;
    int flow = 0, y, t;
    for (int i = cur[x]; i != -1 && flow < lim; i = e[i].ne)
    {
        cur[x] = i;
        if (!vis[y = e[i].ver] && dis[y] == dis[x] + e[i].c && e[i].w)
        {
            if (!(t = find(y, std::min(lim - flow, e[i].w)))) continue;
            e[i].w -= t, e[i ^ 1].w += t, flow += t, mincost += t * e[i].c;
        }
    }
    vis[x] = false;
    return flow;
}
void mcmf()
{
    maxflow = mincost = 0;
    int flow;
    while (spfa()) while(flow = find(S, INF)) maxflow += flow;
}
int main()
{
    scanf("%d %d %d %d", &n, &m, &S, &T);
    memset(h, -1, sizeof h);
    for (int a, b, c, d; m--; dad(a, b, c, d)) scanf("%d %d %d %d", &a, &b, &c, &d);
    mcmf();
    printf("%lld %lld\n", maxflow, mincost);
    return 0;
}

Dijkstra实现

由于dij不能处理负全，必须像Johns全源最短路一样用一个势能来转换为正权

首先跑一次最短路，求出源点到每个点的最短距离 $h_i$ （也是该点的初始势能），接下来和Johnson算法一样，对于一条从 $u$ 到 $v$ ，单位费用为 $w$ 的边，将其边权重置为 $w+h_u-h_v$

可以发现，这样设置势能后新网络上的最短路径和原网络上的最短路径一定对应，不妨设一条从 $S$ 到 $T$ 的路径为 $S\rightarrow p_1\rightarrow p_2\rightarrow…\rightarrow p_k\rightarrow T$ ，则其重表权值后，路径权值和为
$$
\begin{align}
&(w(S,p_1)+ h_S-h_{p_1})+ (w(p_1,p_2)+ h_{p_1}- h_{p_2}) + … + (w(p_k,T) + h_{p_k}-h_T)\\
=&w(S,p_1) + w(p_1,p_2) + … + w(p_k,T) + h_S - h_T
\end{align}
$$
可以发现 $S$ 到 $T$ 的所有路径的相对大小不变

代码：

以前的码风，另外，实测 dij 比 spfa 快大概一倍

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int N = 5000 + 5, M = 50000 + 5, INF = 0x3f3f3f3f;
int S, T, n;
struct Edge
{
	int ne, ver, w, c;
} e[M << 1];
struct Node
{
	int dis, id;
	bool operator<(const Node &t) const
	{
		return dis > t.dis;
	}
}; 
int h[N], idx = 0;
int dis[N], cur[N];
bool v[N], vfind[N]; //为find单独开一个v
int pe[N]; //potential energy,势能
int maxflow, mincost;
void add(int x, int y, int z, int c)
{
	e[idx].ver = y, e[idx].w = z, e[idx].c = c, e[idx].ne = h[x], h[x] = idx++;
}
void addd(int x, int y, int z, int c) //add-double
{
	add(x, y, z, c), add(y, x, 0, -c);
}
void spfa()
{
	queue<int> q;
	for (int i = 1; i <= n; ++i)
		pe[i] = INF;
	q.push(S);
	pe[S] = 0;
	v[S] = true;
	int x, y;
	while (!q.empty())
	{
		x = q.front(), q.pop();
		v[x] = false;
		for (int i = h[x]; i != -1; i = e[i].ne)
		{
			y = e[i].ver;
			if (pe[y] > pe[x] + e[i].c && e[i].w)
			{
				pe[y] = pe[x] + e[i].c;
				if (!v[y])
				{
					v[y] = true;
					q.push(y);
				}
			}
		}
	}
}
bool dij()
{
	priority_queue<Node> q;
	for (int i = 1; i <= n; ++i)
		dis[i] = INF, v[i] = false, cur[i] = h[i];
	dis[S] = 0;
	q.push((Node){0, S});
	int x, y, nc;
	while (!q.empty())
	{
		x = q.top().id, q.pop();
		if (v[x])
			continue;
		v[x] = true;
		for (int i = h[x]; i != -1; i = e[i].ne)
		{
			y = e[i].ver, nc = e[i].c + pe[x] - pe[y];
			if (dis[y] > dis[x] + nc && e[i].w)
			{
				dis[y] = dis[x] + nc;
				if (!v[y])
					q.push((Node){dis[y], y});
			}
		}
	}
	return dis[T] != INF;
}
int find(int x, int limit)
{
	if (x == T)
		return limit;
	vfind[x] = true;
	int flow = 0, y, t, nc;
	for (int i = cur[x]; i != -1 && flow < limit; i = e[i].ne)
	{
		cur[x] = i;
		y = e[i].ver, nc = e[i].c + pe[x] - pe[y];
		if (!vfind[y] && dis[y] == dis[x] + nc && e[i].w)
		{
			t = find(y, min(limit - flow, e[i].w));
			if (!t)
				continue;
			e[i].w -= t;
			e[i ^ 1].w += t;
			flow += t;
			mincost += t * e[i].c;
		}
	}
	vfind[x] = false;
	return flow;
}
void mcmf()
{
	maxflow = mincost = 0;
	int flow;
	while (dij())
	{
		while (flow = find(S, INF))
			maxflow += flow;
		for (int i = 1; i <= n; ++i) //记得每次更新势能
			pe[i] += dis[i];
	}
}
int main()
{
	int m;
	scanf("%d%d%d%d", &n, &m, &S, &T);
	for (int i = 1; i <= n; ++i)
		h[i] = -1;
	for (int i = 1, u, v, w, c; i <= m; ++i)
	{
		scanf("%d%d%d%d", &u, &v, &w, &c);
		addd(u, v, w, c);
	}
	spfa();
	mcmf();
	printf("%d %d\n", maxflow, mincost);
	return 0;
}

最高标号预流推进

最高标号预流推进（High Level Preflow Push，即HLPP）是另一种网络流算法，该算法较Dinic更为高效，然而常数更大

HLPP并不是像Dinic和EK一样基于增广路的算法，它用另外一种更直观的方法求最大流

预流推进

想象一下，如果给到一个网络流让你手算，你咋办？当然是贪心地从源点开始往死里流，尽可能的把每条边流满，如果超过容量就减掉超过部分，一直推到汇点（应该很好理解，可以自己手推试试）

PP也是基于以上思想，用一个队列储存待维护的点（初始时只有 $S$ ），对于每一个当前点，把它有的流量尽可能地推往与之相连的点，然后将相连的点也加入队列

但这样明显有一个问题：可能出现两个点一个推过来一个推回去，结果就死循环了，为了不死循环，我们类似Dinic，引入一个高度 $hi$ ， $hi[S]=n,hi[T]=0$ 规定只能由高为 $hight$ 的点流向高为 $hight-1$ 的点，如果遇到一个点有多余的流量无法流出，就尝试将其抬高一个高度（我们把这个操作叫做重贴标签），直到最后高为 $n+1$ 流回 $S$

最高标号

令人讨厌的、让人无奈的、使人疯魔的Tarjan和他的同事Goldberg在1986年提出了最高标号（HL）预留推进算法，即把普通队列换成优先队列，每次取出高度最高的那个来推进，可以理解为先将高处的点的水移到低处，那么给低处节点推流时可以顺便带走，Cheriyan和Maheshwari在1988年证明了这样做的复杂度为 $O(n^2\sqrt{m})$

优化

虽然上述的算法是正确的，并且复杂度是稳定的（不像某玄学Dinic），但是因为缺少一些优化，使得其上界比较紧，因此在随机数据下可能不如增广路算法，所以下面介绍一些优化

首先是喜闻乐见的gap优化：如果我们发现在给一个点抬高一的高度的时候，这个点原来的高度已经没有点了（出现断层），那么我们直接把大于这个高度的点的高度全部设 $n+1$ ，让他们回流到源点去，因为有了断层，他们无法再有机会把水推到汇点（为什么不能有下面一个点抬上来形成路径呢？因为一个点的高度是所有相邻点高度最小值加一，所以不可能出现这种情况）

其次，我们发现将所有非源点的高度设置为0是有些浪费的。我们不妨通过一遍bfs将每个点的初始高度设置为它到汇点 $T$ 的最短距离，这样就节省了大量重贴标签操作。当然，源点 $S$ 的高度还是应该设置为 $n$

然后，我们发现完全没有必要用优先队列的 $O(\log{n})$ 来求最高点，因为高度最大也就 $n+1$ ，完全可以用一个桶存下所有高度的节点，$O(1)$ 得到最高点

代码

模板

以前码风版：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int N = 1200 + 5, M = 120000 + 5, INF = 0x3f3f3f3f;
int n, m, S, T;
struct Edge
{
	int ne, ver, w;
} e[M << 1];
int h[N], idx = 0;
int hi[N], ex[N], gap[N]; //hi:高度,ex:超额流,gap[i]:高度为i的节点的数量
vector<int> B[N]; // 桶B[i]中记录所有hi[x]=i的x
int level = 0; //溢出节点的最高高度
void add(int x, int y, int z)
{
	e[idx] = (Edge){h[x], y, z}, h[x] = idx++;
}
void addd(int x, int y, int z)
{
    add(x, y, z), add(y, x, 0);
}
bool bfs()
{
	queue<int> q;
	for (int i = 1; i <= n; ++i)
		hi[i] = INF;
	hi[T] = 0;
	q.push(T);
	int x, y;
	while (!q.empty())
	{
		x = q.front(), q.pop();
		for (int i = h[x]; i != -1; i = e[i].ne)
		{
			y = e[i].ver;
			if (e[i ^ 1].w && hi[y] > hi[x] + 1) //从T倒着搜回去走的是反向边,^1以后就变回正向边
				hi[y] = hi[x] + 1, q.push(y);
		}
	}
	return hi[S] != INF;
}
int push(int x) //尽可能通过能够推送的边推送超额流
{
	bool init = x == S;
	for (int i = h[x], y, k; i != -1; i = e[i].ne)
	{
		y = e[i].ver;
		if (!e[i].w || (init == false && hi[x] != hi[y] + 1)) //初始化时不考虑高度差为1
			continue;
		k = init ? e[i].w : min(e[i].w, ex[x]); //取到剩余容量和超额流的最小值初始化时可以使源的溢出量为负数
		if (y != S && y != T && !ex[y])
			B[hi[y]].push_back(y), level = max(level, hi[y]);
		ex[x] -= k, ex[y] += k, e[i].w -=k, e[i ^ 1].w += k;
		if (!ex[x]) //如果已经推送完就返回
			return 0;
	}
	return 1;
}
void relabel(int x)  //重贴标签(高度)
{
  hi[x] = INF;
  for (int i = h[x]; i != -1; i = e[i].ne)
    if (e[i].w)
		hi[x] = min(hi[x], hi[e[i].ver]);
  if (++hi[x] < n) //只处理高度小于n的节点
  {
	  //新的高度,更新gap
	  B[hi[x]].push_back(x);
	  level = max(level, hi[x]);
	  ++gap[hi[x]];  
  }
}
int find_max() //选出当前高度最大的节点之一,如果已经没有溢出节点返回0
{
	while (B[level].empty() && level > -1)
		--level;
	return level == -1 ? 0 : B[level].back();
}
int hlpp()
{
	if (!bfs())
		return 0;
	for (int i = 1; i <= n + 1; ++i)
		gap[i] = 0;
	for (int i = 1; i <= n; ++i)
		if (hi[i] != INF)
			++gap[hi[i]];
	hi[S] = n;
	push(S); //初始化预流
	int x;
	while (x = find_max())
	{
		B[level].pop_back();
		if (push(x)) //仍然溢出
		{
			if (!--gap[hi[x]])
				for (int i = 1; i <= n; ++i)
					if (i != S && i != T && hi[i] > hi[x] && hi[i] < n + 1)
						hi[i] = n + 1;  // 这里重贴成 n+1 的节点都不是溢出节点
      		relabel(x);
		}
	}
	return ex[T];
}
int main()
{
	int m;
	scanf("%d%d%d%d", &n, &m, &S, &T);
	for (int i = 1; i <= n; ++i)
		h[i] = -1;
	for (int i = 1, u, v, w, c; i <= m; ++i)
	{
		scanf("%d%d%d", &u, &v, &w);
		addd(u, v, w);
	}
	printf("%d\n", hlpp());
	return 0;
}

now：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
#include <bits/stdc++.h>
using LL = long long;
const int N = 1200 + 5, M = 1.2e5 + 5, INF = 0x3f3f3f3f;
int n, m, S, T;
struct Edge{ int ne, ver, w; } e[M << 1];
int h[N], idx = 0, hi[N], gap[N], lvl = 0, ex[N];
std::vector<int> B[N];
void add(int x, int y, int z){ e[idx] = {h[x], y, z}, h[x] = idx++; }
void dad(int x, int y, int z){ add(x, y, z), add(y, x, 0); }
bool bfs()
{
    std::queue<int> q;
    memset(hi, 0x3f, sizeof hi);
    hi[T] = 0, q.push(T);
    for (int x, y; !q.empty(); )
    {
        x = q.front(), q.pop();
        for (int i = h[x]; i != -1; i = e[i].ne)
            if (e[i ^ 1].w && hi[y = e[i].ver] > hi[x] + 1) hi[y] = hi[x] + 1, q.push(y);
    }
    return hi[S] != INF;
}
bool puf(int x) //push flow
{
    bool init = x == S;
    for (int i = h[x], y, k; i != -1; i = e[i].ne)
    {
        y = e[i].ver; //这句不能压行
        if (!e[i].w || (!init && hi[x] != hi[y] + 1)) continue;
        k = init ? e[i].w : std::min(e[i].w, ex[x]);
        if (y != S && y != T && !ex[y]) B[hi[y]].push_back(y), lvl = std::max(lvl, hi[y]);
        ex[x] -= k, ex[y] += k, e[i].w -= k, e[i ^ 1].w += k;
        if (!ex[x]) return false;
    }
    return true;
}
void rel(int x)
{
    hi[x] = INF;
    for (int i = h[x]; i != -1; i = e[i].ne) if (e[i].w) hi[x] = std::min(hi[x], hi[e[i].ver]);
    if (++hi[x] < n)
    {
        B[hi[x]].push_back(x);
        lvl = std::max(lvl, hi[x]);
        ++gap[hi[x]];
    }
}
int getmx()
{
    while (B[lvl].empty() && lvl >= 0) --lvl;
    return lvl == -1 ? 0 : B[lvl].back();
}
int hlpp()
{
    if (!bfs()) return 0;
    memset(gap, 0, sizeof gap);
    for (int i = 1; i <= n; ++i) if (hi[i] != INF) ++gap[hi[i]];
    hi[S] = n, puf(S);
    for (int x; x = getmx(); )
    {
        B[lvl].pop_back();
        if (puf(x))
        {
            if (!--gap[hi[x]]) 
                for (int i = 1; i <= n; ++i)
                    if (i != S && i != T && hi[i] > hi[x] && hi[i] <= n) hi[i] = n + 1;
            rel(x);
        }
    }
    return ex[T];
}
int main()
{
    scanf("%d %d %d %d", &n, &m, &S, &T);
    memset(h, -1, sizeof h);
    for (int a, b, c; m--; dad(a, b, c)) scanf("%d %d %d", &a, &b, &c);
    printf("%d\n", hlpp());
}

结语

一般来说好用又好打的Dinic已经足够，但HLPP在加上优化后完虐Dinic，但不管是哪个，需要注意有可能的最大流炸int的情况