老缝合怪了

笛卡尔树

定义

笛卡尔树是一种二叉树， 每个节点有一个键值二元组 $(k,w)$ ，其中 $k$ 满足二叉搜索树的性质，而 $w$ 满足堆的性质，我知道你和我一样没看懂所以，看图：

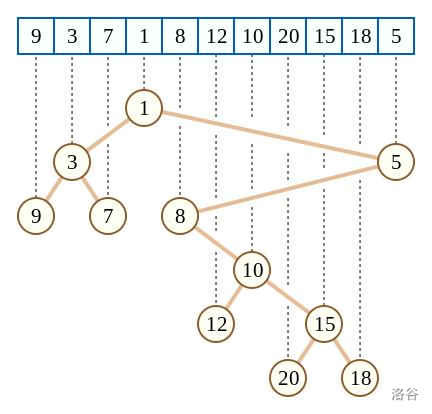
上图是一棵笛卡尔树， $k$ 是下标， $w$ 是权值，则图中的树既满足二叉搜索树的性质（ $r$ 左子树的节点下标小于 $r$ ，右子树的节点下标大于 $r$ ），也满足一个小根堆（父节点的权值小于子节点）

当然上图是一种特殊的（也是常用的）笛卡尔树，它的键值 $k$ 恰好是数组下标，这使得它有一个性质：一棵子树内的下标是连续的一个区间（这样才能满足二叉搜索树的性质）

构建

构建一棵笛卡尔树无非就两种思路：

一、保证堆性质的情况下构造二叉搜索树

其实基本不会这么写……只是提一提

以小根堆为例，每次找到最小值（记其位置为 $pos$ ）作为当前子树的根，再递归处理左子树 $[l,pos-1]$ ，右子树 $[pos+1,r]$ ，找最小值可以ST表优化，时间复杂度 $O(n\log n)$ 显然不能接受

二、保证二叉搜索树性质的情况下构造堆

这才是正道

考虑将元素按照键值 $k$ 排序（如果 $k$ 是下标显然不用排序了），然后一个一个插入到当前的笛卡尔树中，则每次我们插入当前节点时，一定是插入到当前树的最右端（一直向右子树走直到无法再走），这样才满足二叉搜索树的性质（我们称根节点到最右端的节点构成的链为右链）

但我们又必须满足堆性质，所以我们执行如下操作：从下往上比较比较右链结点（设为 $x$ ）与当前新插入结点（设为 $u$ ）的权值，若找到节点 $x$ 满足 $x_w<u_w$ ，就把 $u$ 接到 $x$ 的右儿子上（这样满足了堆性质），然后把原来 $x$ 的右子树变成 $u$ 的左子树（这样满足了二叉搜索树性质），具体如图：

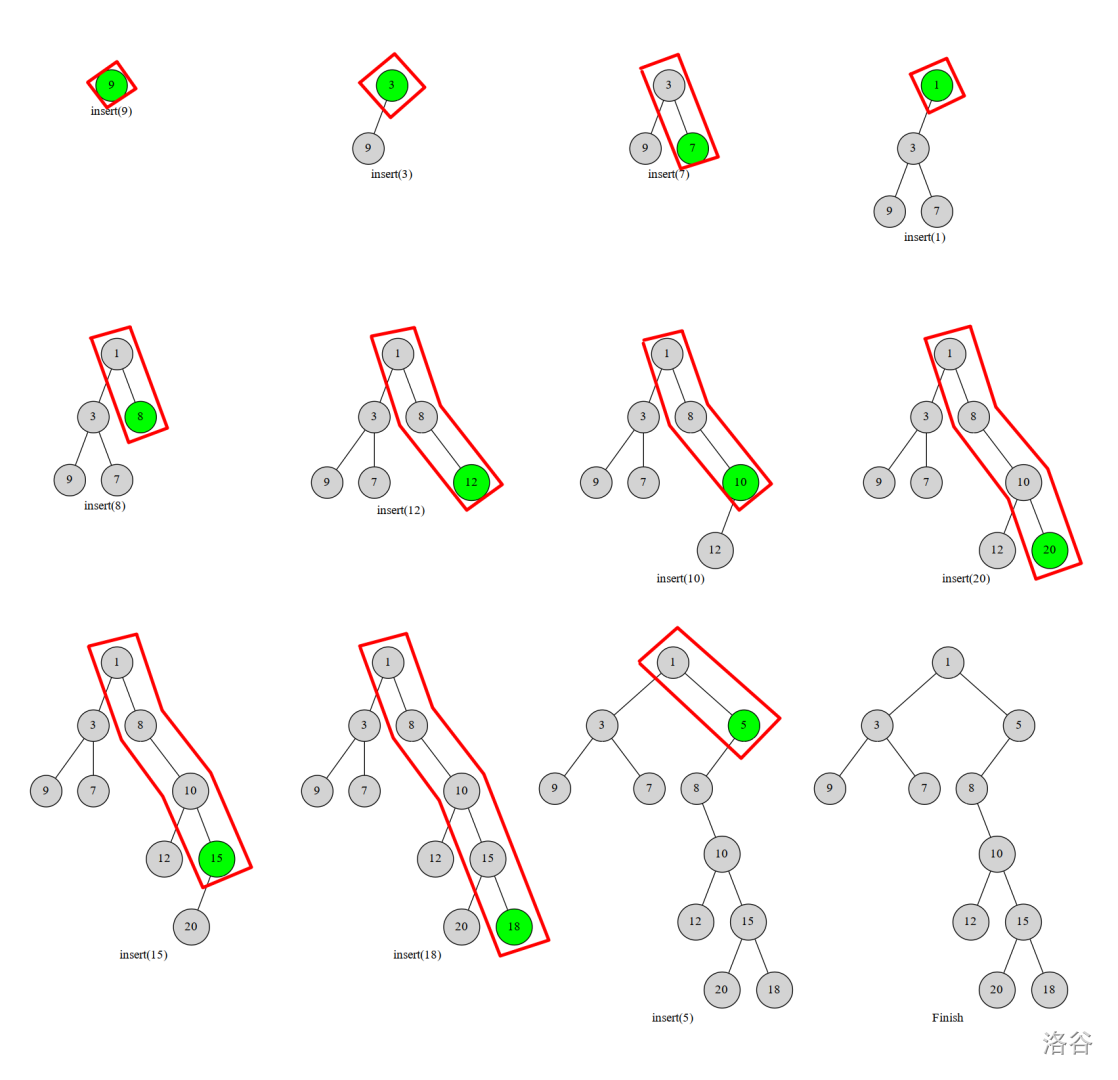
这样，我们发现我们维护的其实是当前树的右链（图中红色部分），可以用一个单调栈维护，每个节点显然最多进出栈一次，时间复杂度为 $O(n)$

代码如下：

建树

#include <bits/stdc++.h>
using namespace std;
const int N = 10000000 + 5;
int n;
int a[N];
struct CartesianTree
{
	int dat, lc, rc;
} tr[N];
long long ans;
int stk[N], top = 0; //数组太大,开在函数里会爆栈
void build()
{
	for (int i = 1; i <= n; ++i)
		tr[i].dat = a[i];
	for (int i = 1, k; i <= n; ++i)
	{
		k = top;
		//找到最下面的一个比当前小的,满足小根堆
		while (k > 0 && tr[stk[k]].dat > tr[i].dat)
			--k;
		if (k)
			tr[stk[k]].rc = i;
		if (k < top)
			tr[i].lc = stk[k + 1];
		top = k;
		stk[++top] = i;
	}
}
int main()
{
	// freopen("t.in", "r", stdin);
	// freopen("t.out", "w", stdout);
	scanf("%d", &n);
	for (int i = 1; i <= n; ++i)
		scanf("%d", &a[i]);
	build();
	ans = 0;
	for (int i = 1; i <= n; ++i)
		ans ^= (long long)i * (tr[i].lc + 1);
	printf("%lld ", ans);
	ans = 0;
	for (int i = 1; i <= n; ++i)
		ans ^= (long long)i * (tr[i].rc + 1);
	printf("%lld", ans);
	return 0;
}

有些时候我们甚至不必建出树，直接用单调栈即可