暴搜能过样例了!
模拟退火(Simulated Annealing)
思想
模拟退火是一种启发式的随机暴力算法,主要用于解决最优化问题。
基本概念
- 温度:决定每次随机时我们随机的范围,温度越大,下一个点的随机区间越大,在模拟退火中,温度总是不断减小,一般把温度记为 $T$ ;
- 初始温度:最初的温度值;
- 终止温度:结束时的温度;
- 衰减方式:每次温度的变化,可以是一次(如 $T_i=T_{i-1}-c$ ),也可以是指数级(如 $T_i=T_{i-1}*c,c\in (0,1)$ )等,根据实际情况而定,但一般要保证 $T_i<T_{i-1}$ ;
- 能量值:当前答案的“权值”,或者说“优秀程度”,能量值越小,答案越优,个人喜欢记答案 $x$ 的能量值为 $E(X)$ ;
算法过程
- 确定初始点(初始答案),初始温度为 $T_0$ (一般保证足够大),终止温度 $T_e$ (一般保证足够小),衰减方式;
- 在当前点(设为 $now$ )温度范围内随机选择一个值 $np$ ,计算答案 $E(np)$ ,记 $E(np)-E(now)=\Delta E$ ;
- 若 $\Delta E < 0$ ,说明 $np$ 比 $now$ 优,则跳转到 $np$ ;
- 若 $\Delta E > 0$ ,则以一定的概率跳转到 $np$ ,一般来说,这个概率取成 $e^{-\frac{\Delta E}{T}}$ ,这样取的好处是 $np$ 比 $now$ 越差,我们跳转过去的概率越小 ;
例题一
A Star not a Tree?
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
| #include<bits/stdc++.h>
using namespace std;
const int N=100+5,INF=0x3f3f3f3f;
const double T0=10000+5,TE=1e-4,C=0.99;
int n;
int T;
struct Node{
double x,y;
void inint(double _x,double _y){
x=_x;
y=_y;
}
}q[N];
double ans=INF;
double rand_d(double l,double r){
return (double)rand()/RAND_MAX*(r-l)+l;
}
double get_dist(Node x,Node y){
double dx=x.x-y.x;
double dy=x.y-y.y;
return sqrt(dx*dx+dy*dy);
}
double E(Node x){
double res=0;
for(int i=1;i<=n;++i) res+=get_dist(x,q[i]);
ans=min(ans,res);
return res;
}
void simulate_anneal(){
Node now;
now.inint(rand_d(0,T0),rand_d(0,T0));
for(double t=T0;t>TE;t*=C){
Node np;
np.inint(rand_d(now.x-t,now.x+t),rand_d(now.y-t,now.y+t));
double dt=E(np)-E(now);
if(exp(-dt/t)>rand_d(0,1)) now=np;
}
}
int main(){
scanf("%d",&T);
while(T--){
ans=INF;
scanf("%d",&n);
for(int i=1;i<=n;++i) scanf("%lf%lf",&q[i].x,&q[i].y);
for(int i=1;i<=100;++i) simulate_anneal();
printf("%.0lf\n",ans);
if(T!=0) printf("\n");
}
return 0;
}
|
例题二
模拟退火不只能解决那些数学模型非常明显的题目,也可以解决一些其他最优化问题,只要保证答案具有“连续性”(即设 $\gamma$ 是大于 $0$ 且足够小的实数, $\forall x$ ,有 $|E(x)-E(x+ \gamma)|$ 足够小)。
看看这题保龄球
对于这种给数列 $A$ ,求 $A$ 的某种最优排列的问题,我们可以思考如何使用模拟退火:
- 温度可以直接像上题一样设置,衰减也可以自设;
- 初始点(初始排列)就用题目给的原排列,每次转移时在原排列上随机两个位置交换,得到下一个排列;
- 依题意打估价函数 $E(x)$ ,估价并概率转移;
由上,我们发现本题可以轻松用退火解决。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
| #include<bits/stdc++.h>
using namespace std;
const int N=50+5,INF=0x3f3f3f3f;
const double T0=1e4+5,TE=1e-4,C=0.99;
int n,m;
int ans=-INF;
struct Try{
int x,y;
}q[N];
int E(){
int res=0;
for(int i=1;i<=m;++i){
res+=q[i].x+q[i].y;
if(i<=n){
if(q[i].x==10) res+=q[i+1].x+q[i+1].y;
else if(q[i].x+q[i].y==10) res+=q[i+1].x;
}
}
ans=max(ans,res);
return -res;
}
void simulate_anneal(){
for(double t=T0;t>TE;t*=C){
int a=rand()%m+1,b=rand()%m+1;
int now=E();
swap(q[a],q[b]);
if(n+(q[n].x==10)==m){
int np=E();
int dt=np-now;
if(exp(-dt/t)<(double)rand()/RAND_MAX) swap(q[a],q[b]);
}
else swap(q[a],q[b]);
}
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;++i) scanf("%d%d",&q[i].x,&q[i].y);
if(q[n].x==10) m=n+1,scanf("%d%d",&q[m].x,&q[m].y);
else m=n;
while((double)clock()/CLOCKS_PER_SEC<0.8) simulate_anneal();
printf("%d\n",ans);
return 0;
}
|
例题三
一道类似于上题的排列退火,但加入一定的优化
均分数据
这道题直接模拟退火也能过,但略显的有点过于暴力,我们可以考虑模拟退火加一点贪心(当然也可以加DP,但那样还不如直接用DP,我就是做不出DP才模拟退火的好吧):
先用退火得到数列的排列,计算当前答案时,对于当前数 $a_i$ ,我们每次都将 $a_i$ 放到当前和最小的集合中,贪心计算。可以证明,虽然我不会证,这样贪心是不会漏掉最优解的。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| #include<bits/stdc++.h>
using namespace std;
const int N=20+5,M=10,INF=0x3f3f3f3f;
const double T0=1e4+5,TE=1e-6,C=0.99;
int n,m;
int w[N],s[M];
double ans=INF;
double E(){
for(int i=1;i<=m;++i) s[i]=0;
for(int i=1,k=1;i<=n;++i){
for(int j=1;j<=m;++j) if(s[j]<s[k]) k=j;
s[k]+=w[i];
}
double avg=0;
for(int i=1;i<=m;++i) avg+=(double)s[i]/m;
double res=0;
for(int i=1;i<=m;++i) res+=(s[i]-avg)*(s[i]-avg);
res=sqrt(res/m);
ans=min(ans,res);
return res;
}
void simulate_anneal(){
random_shuffle(w+1,w+1+n);
for(double t=T0;t>TE;t*=C){
int a=rand()%n+1,b=rand()%n+1;
double x=E();
swap(w[a],w[b]);
double y=E();
double dt=y-x;
if(exp(-dt/t)<(double)rand()/RAND_MAX) swap(w[a],w[b]);
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;++i) scanf("%d",&w[i]);
while((double)clock()/CLOCKS_PER_SEC<0.8) simulate_anneal();
printf("%.2lf\n",ans);
return 0;
}
|
以上两个题都用了 $while((double)clock()/CLOCKS_PER_SEC<0.8)$ 来控制退火次数,在实际做题时,一般计算好循环次数的代码会更稳定一些,但如果不好估算循环次数,这样也不失为一种选择。
爬山法
对于一个凸函数(单峰函数),我们可以用爬山法解决(当然,和退火一样,不是要求题目有明确的函数模型,只是需要答案对于每一维自变量你能感觉到一个单峰函数即可,有点玄学)。
爬山法的思路大体如图:
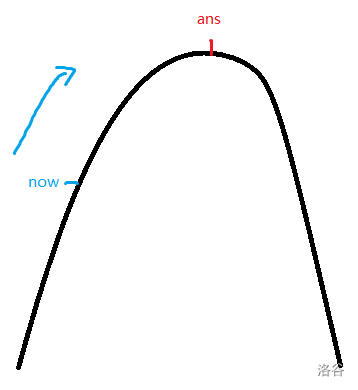
对于点 $now$ 我们并不关心它对应的具体值是多少,我们只关心它去向答案的“方向”(如图中应该是蓝色箭头方向),然后我们只需要向着“方向”走即可,图中是一个维度,而多个维度就分每个维度单独计算“方向”即可。当然,走的“距离”视具体情况而定。
需要注意的是,爬山法局限较多,不太常用,但仍不失为一种很好的启发式算法。
例题一
球形空间产生器
本题正解是高斯消元,建立方程联立求解即可,但如果你和我一样高斯消元和矩阵学的不好,也可以用爬山法搞定。
我们发现对于 $n$ 维坐标的每一维,都是一个单峰函数(球心到各点距离相等),所以对于一个可能答案的一维,求它到各点的距离的平均值,距离大于平均值的点表现出拉力,反之为推力,将所有力合成即可。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| #include<bits/stdc++.h>
using namespace std;
const int N=20+5;
int n;
double d[N][N];
double ans[N],dis[N],delta[N];
void calc(){
double avg=0;
for(int i=1;i<=n+1;++i){
dis[i]=delta[i]=0;
for(int j=1;j<=n;++j)
dis[i]+=(d[i][j]-ans[j])*(d[i][j]-ans[j]);
dis[i]=sqrt(dis[i]);
avg+=dis[i]/(n+1);
}
for(int i=1;i<=n+1;++i)
for(int j=0;j<=n;++j)
delta[j]+=(dis[i]-avg)*(d[i][j]-ans[j])/avg;
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n+1;++i)
for(int j=1;j<=n;++j){
scanf("%lf",&d[i][j]);
ans[j]+=d[i][j]/(n+1);
}
for(double t=1e4;t>1e-6;t*=0.99997){
calc();
for(int i=1;i<=n;++i) ans[i]+=delta[i]*t;
}
for(int i=1;i<=n;++i) printf("%.3lf ",ans[i]);
return 0;
}
|
当然,此题用模拟退火也行,代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
| #include<bits/stdc++.h>
using namespace std;
const int N=10+5,INF=0x3f3f3f3f;
const double T0=1e4+5,TE=1e-6,C=0.99995;
int n;
struct Node{
double x[N];
Node operator+(const Node &_t) {
Node res;
for(int i=1;i<=n;++i) res.x[i]=x[i]+_t.x[i];
return res;
}
}q[N],ans;
double as=INF;
double s[N];
Node now,np;
double rand_d(double l,double r){
return (double)rand()/RAND_MAX*(r-l)+l;
}
double get_dist(Node x,Node y){
double res=0;
for(int i=1;i<=n;++i) res+=(x.x[i]-y.x[i])*(x.x[i]-y.x[i]);
return sqrt(res);
}
double E(Node x){
double avg=0;
for(int i=1;i<=n+1;++i){
s[i]=get_dist(x,q[i]);
avg+=s[i];
}
avg=avg/(n+1);
double res=0;
for(int i=1;i<=n+1;++i) res+=(s[i]-avg)*(s[i]-avg);
res*=avg;
if(res<as){
as=res;
ans=x;
}
return res;
}
void simulate_anneal(){
for(int i=1;i<=n+1;++i) now=now+q[i];
for(int i=1;i<=n;++i) now.x[i]=now.x[i]/(n+1);
for(double t=T0;t>TE;t*=C){
for(int i=1;i<=n;++i) np.x[i]=now.x[i]+rand_d(-t,t);
double dt=E(np)-E(now);
if(exp(-dt/t)>rand_d(0,1)) now=np;
}
}
int main(){
srand(time(0));
scanf("%d",&n);
for(int i=1;i<=n+1;++i)
for(int j=1;j<=n;++j)
scanf("%lf",&q[i].x[j]);
simulate_anneal();
for(int i=1;i<=n;++i) printf("%.3lf ",ans.x[i]);
return 0;
}
|
牛顿迭代法
对于维度少的单峰函数,除了用三分法求最值外,也可用牛顿迭代法(又名牛顿爬山法)
牛顿迭代法的核心公式是
$$
x_{i+1}=x_i-\frac{f(x_i)}{f’(x_i)}
$$
但牛顿迭代法有一个巨大的缺陷——我这么弱根本求不出导函数来,笑死。
