Dyd's Blog

He who has a strong enough why can bear almost any how.

斜率优化dp

Posted on Edited on In
Symbols count in article: 4.2k Reading time ≈ 4 mins.

然而我dp废的一比

用例题开讲：
P2365 任务安排
明显看题解可知，dp方程为：
$f_i=min(f_j+sumt_i*(sumc_i-sumc_j)+s*(sumc_n-sunc_j),f_i)$
故标程如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
//P2365
#include <bits/stdc++.h>
using namespace std;
const int N = 5000 + 5;
struct Sum
{
    int t, c;
} sum[N];
int n, s;
int f[N];
int main()
{
    scanf("%d%d", &n, &s);
    for (int i = 1; i <= n; ++i)
    {
        int t, c;
        scanf("%d%d", &t, &c);
        sum[i].t = sum[i - 1].t + t;
        sum[i].c = sum[i - 1].c + c;
    }
    memset(f, 0x3f, sizeof f);
    f[0] = 0;
    for (int i = 1; i <= n; ++i)
        for (int j = 0; j < i; ++j)
            f[i] = min(f[i], f[j] + sum[i].t * (sum[i].c - sum[j].c) + s * (sum[n].c - sum[j].c));
    printf("%d", f[n]);
    return 0;
}

那么，康康这个——P5785 SDOI2012任务安排
令人惋惜的是，在数据加强后， $O(n^2)$ 的时间复杂度似乎确凿过不了，为此，我们看题解后想到救星——

斜率优化

我们先假设所有的 $t$ 都大于0。
我们来康康转移方程：
$f_i=min(f_j+sumt_i*(sumc_i-sumc_j)+s*(sumc_n-sunc_j),f_i)$
不妨去掉 $min$ 看成：
$f_i=f_j+sumt_i*(sumc_i-sumc_j)+s*(sumc_n-sunc_j)$
它等价于：
$f_i=f_j-(sumt_i+s) * sumc_j+sumt_i* sumc_i+s* sumc_n$
设 $f_j=y,sumc_j=x$ （这是所有的关于 $j$ 的变量），然后化为直线表达式 $y=kx+b$ 的形式：
$f_j=(sumt_i+s)* sumc_j+f_i-sumt_i* sumc_i-s* umc_n$
不难发现 ：

  1. $k=sumt_i+s$ ，故 $0<k<\infty$ 。

  2. 且 $0 \le j \le i-1,j \in Z$

  3. 而直线上的点为：$(f_0,sumc_0)$ 、 $(f_1,sumc_1)$ 、 … 、 $(f_{i-1},sunc_{i-1})$

  4. 我们的目标是让 $f_i$ 最小

我们带着目标，看看图像：
xoy
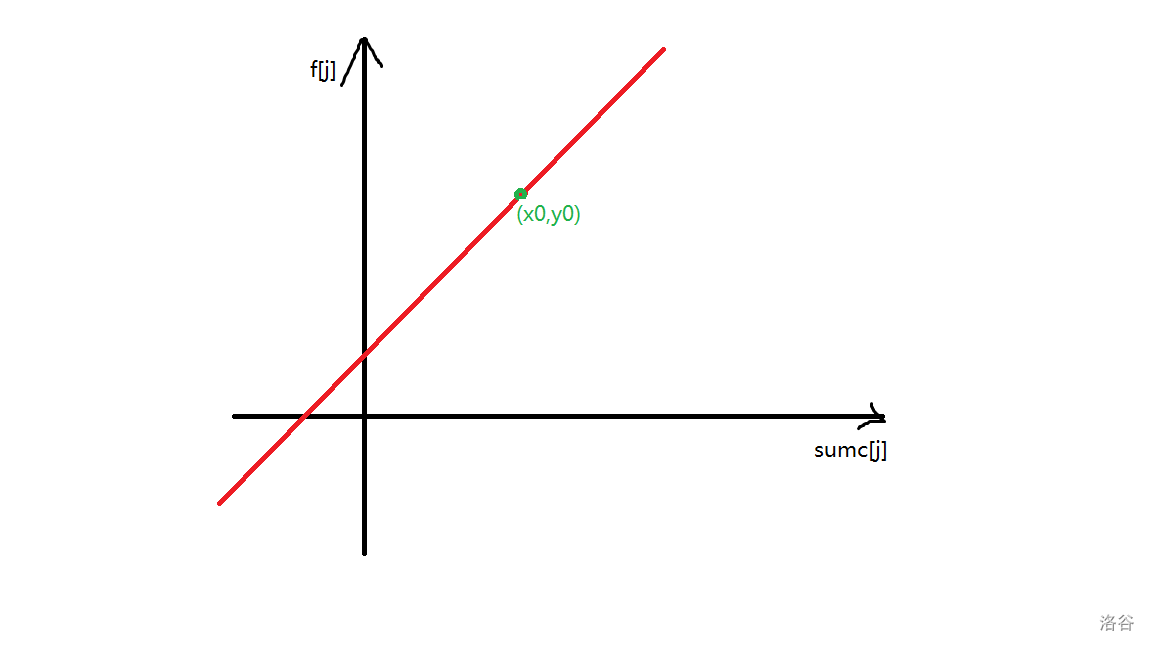
对于一个已知的 $i$ ， $k=sumt_i+s$ 是固定的，而若点 $(x_0,y_0)$在 $y=kx+b$ 上，那么截距 $b$ 是可以算出来的，又因 $b=f_i-sumt_i* sumc_i-s* umc_n$ ，故 $b$ 最小时 $f_i$ 最小。
那么，我们康康下图：
xoy2
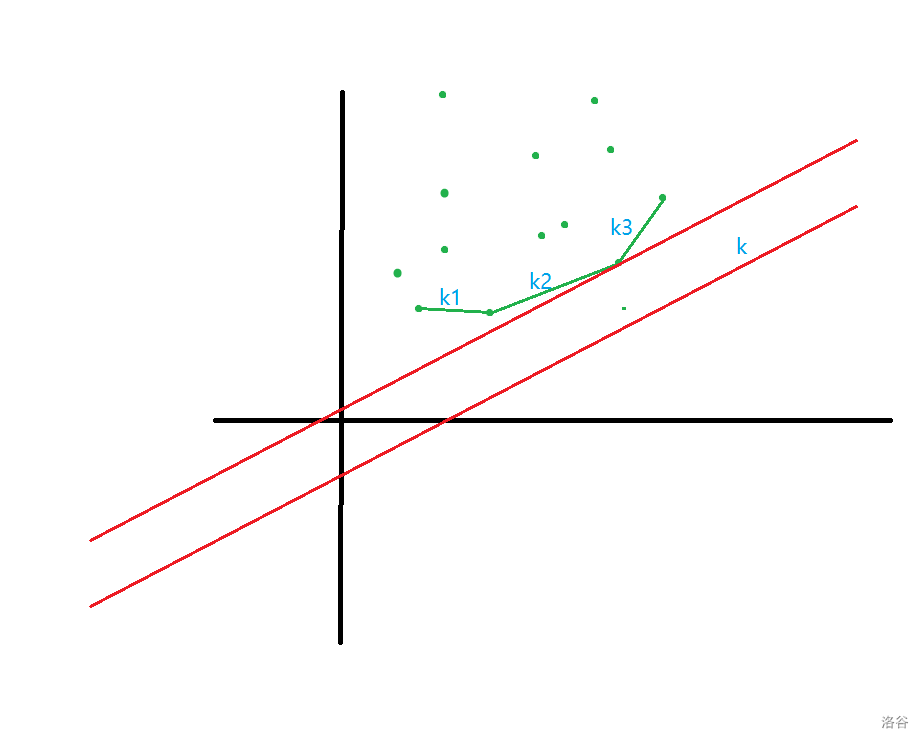
图中绿色的点是所有可能的 $(x_0,y_0)$ ,红色的线是 $y=kx+b$ （只有 $k$ 确定，所以在从下往上平移）。
不难发现，凸包（绿线）内部的点对于 $b$ 的最小值毫无意义。换句话说，最小值的点只会在凸包上。
那么在凸包上哪一点呢？
还是上图，令构成凸包的三条直线斜率为 $k_1,k_2,k_3$ ，由凸包性质可得 $k_1<k_2<k_3$ 。再看看上图中我们要找的那个点（不妨设它为点 $A$ ）， $A$ 所在的两条直线斜率为 $k_2,k_3$ ,且 $k_2<k<k_3$ 也就是说，对于一个给定斜率为的直线 $y=kx+b$ 让它的截距 $b$ 取得最小值的点就是凸包上第一个斜率大于 $k$ 的线段的下端点。
由此，我们想到在单调队列中维护第一个大于某个数的点。
我们又发现，因为 $t$ 大于0，所以：
斜率是单调递增的，且新加的点的横坐标也单调递增。
所以：
在查询的时候，可以将队头小于当前斜率的点全删除掉。
在插入的时候，可以将队尾所有不在凸包上的点全删除掉。
我们便得到以下代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include <bits/stdc++.h>
using namespace std;
const int N = 300000 + 5;
typedef long long ll;
struct Sum
{
    ll t, c;
} sum[N];
ll n, s;
ll f[N];
ll q[N], hh = 0, tt = 0;
//除法会损失精度，故改成乘法
bool check_slopeh(ll x, ll y, ll o)
{
    return (f[y] - sum[y].c * s - f[x] + sum[x].c * s) <= sum[o].t * (sum[y].c - sum[x].c);
}
bool check_slopet(ll x, ll y, ll a, ll b)
{
    return (f[y] - sum[y].c - f[x] + sum[x].c) * (sum[b].c - sum[a].c) >= (f[b] - sum[b].c - f[a] + sum[a].c) * (sum[y].c - sum[x].c);
}
int main()
{
    scanf("%lld%lld", &n, &s);
    for (ll i = 1; i <= n; ++i)
    {
        ll t, c;
        scanf("%lld%lld", &t, &c);
        sum[i].t = sum[i - 1].t + t;
        sum[i].c = sum[i - 1].c + c;
    }
    memset(f, 0x7f, sizeof f);
    f[0] = 0;
    q[0] = 0;
    for (ll i = 1; i <= n; ++i)
    {
        while (hh < tt && check_slopeh(q[hh], q[hh + 1], i))
            hh++;
        ll j = q[hh];
        f[i] = f[j] + sum[i].t * (sum[i].c - sum[j].c) + s * (sum[n].c - sum[j].c);
        while (hh < tt && check_slopet(q[tt - 1], q[tt], q[tt], i))
            tt--;
        q[++tt] = i;
    }
    printf("%lld", f[n]);
    return 0;
}

但是——60分！哦可恶！题目中的 $t$ 可以为负数，咋办？

二分

我们来看看 $t$ 可以为负数的情况：

  1. $k=sumt_i+s$ ，但 $sumt_i$ 可能小于0，故 $ -\infty <k< \infty$ 。

  2. $0 \le j \le i-1,j \in Z$

  3. 而直线上的点为：$(f_0,sumc_0)$ 、 $(f_1,sumc_1)$ 、 … 、 $(f_{i-1},sunc_{i-1})$

  4. 我们的目标是让 $f_i$ 最小

其实只有 $k$ 的范围变了， $k$ 可以小于0了，所以：
斜率不再具有单调性，但新加的点的横坐标仍然单调递增。
所以：
在查询的时候，只能用二分来查找了。
但在插入的时候，仍可以将队尾所有不在凸包上的点全删除掉。
终于，正解如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
//P5785
#include <bits/stdc++.h>
using namespace std;
const int N = 300000 + 5;
typedef long long ll;
struct Sum
{
    ll t, c;
} sum[N];
ll n, s;
ll f[N];
ll q[N], hh = 0, tt = 0;
//除法会损失精度，故改成乘法
bool check_slopeh(ll x, ll y, ll o)
{
	return (f[y] - sum[y].c * s - f[x] + sum[x].c * s) <= sum[o].t * (sum[y].c - sum[x].c);
}
bool check_slopet(ll x, ll y, ll a, ll b)
{
    return (f[y] - sum[y].c - f[x] + sum[x].c) * (sum[b].c - sum[a].c) >= (f[b] - sum[b].c - f[a] + sum[a].c) * (sum[y].c - sum[x].c);
}
ll work(ll o)
{
    ll l = hh, r = tt;
    int ans = l;
    while (l <= r)
    {
        ll mid = l + r >> 1;
        if (!check_slopeh(q[mid], q[mid + 1], o))
            r = mid - 1, ans = mid;
        else
            l = mid + 1;
    }
    return q[ans];
}
int main()
{
    scanf("%lld%lld", &n, &s);
    for (ll i = 1; i <= n; ++i)
    {
        ll t, c;
        scanf("%lld%lld", &t, &c);
        sum[i].t = sum[i - 1].t + t;
        sum[i].c = sum[i - 1].c + c;
    }
    memset(f, 0x7f, sizeof f);
    f[0] = 0;
    q[0] = 0;
    for (ll i = 1; i <= n; ++i)
    {
        ll j = work(i);
        f[i] = f[j] + sum[i].t * (sum[i].c - sum[j].c) + s * (sum[n].c - sum[j].c);
        while (hh < tt && check_slopet(q[tt - 1], q[tt], q[tt], i))
            tt--;
        q[++tt] = i;
    }
    printf("%lld", f[n]);
    return 0;
}