Dyd's Blog

He who has a strong enough why can bear almost any how.

快速傅里叶变换

Posted on Edited on In
Symbols count in article: 8.2k Reading time ≈ 7 mins.

FFT常数比NTT大！

快速傅里叶变换

引入

快速傅里叶变换（FFT）是一种快速求解两个多项式的乘积（或者称之为两个函数的卷积，但注意，这个卷积不是狄拉克雷卷积）的方法

例如已知
$$
\begin{align}
A(x)=a_0+a_1x+a_2x^2+…+a_nx^n\\
B(x)=b_0+b_1x+b_2x^2+…+b_nx^n
\end{align}
$$
求 $A*B$

如果直接计算，复杂度显然为 $O(n^2)$ ，而FFT可以在 $O(n\log{n})$ 的时间求出答案

前置知识：复数

任意一个复数可以表示为 $a+bi$ 的形式，其中 $a$ 被称为实部， $b$ 被称为虚部， $i=\sqrt{-1}$ 是虚数单位

类似于实数可以对应到数轴上，复数可以对应到坐标轴上

复数

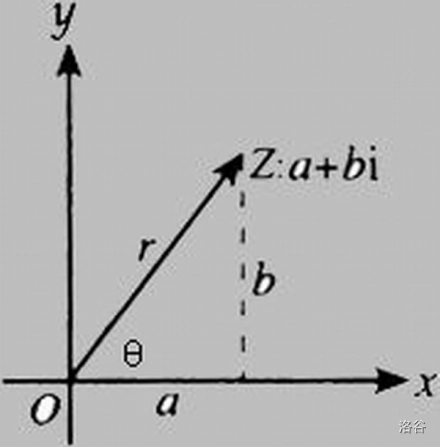
如上图， $X$ 轴表示实部， $Y$ 轴表示虚部，则 $a+bi$ 可对应到唯一的一个点，而 $a+bi$ 也就有了几何意义：一条从原点指向 $(a,b)$ 的向量 ，而该向量与 $X$ 轴的夹角 $\theta$ 被称为该复数的辐角

则复数的运算有以下法则：

  • $(a+bi)+(c+di)=(a+c)+(b+d)i$

    复数加法的几何意义就是向量加法

  • $(a+bi)(c+di)=ac+adi+cbi+bdi^2=(ac-bd)+(ad+cb)i$

    复数乘法有很好的几何意义，两个向量 $\vec{a},\vec{b}$ 的积 $\vec{c}$ 的长度（模）就是两个向量的长度和，即 $|\vec{c}|=|\vec{a}|+|\vec{b}|$ ，积的辐角就是两个向量辐角的和，即 $\theta_c=\theta_a+\theta_b$

在平面直角坐标系 $X0Y$ 中，画一个单位圆，将其等分为 $n$ 份，取其中的 $k$ 份，将原点于 $k$ 份的点连接形成一个向量，记为 $\omega_n^k$ ，我们称 $\omega_n^k$ 为复数域上的 $n$ 次单位根（即方程 $z^n=1$ 的根）

单位根

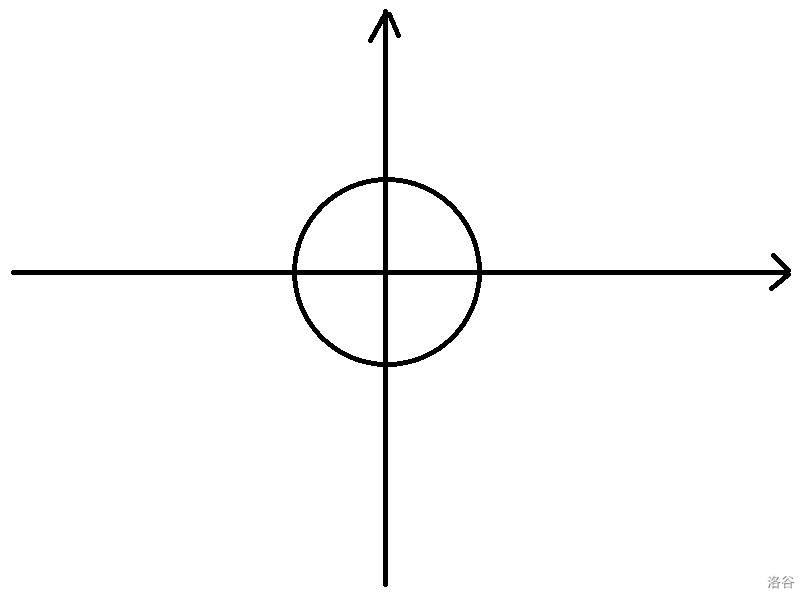
单位根有以下性质：

  • $\forall i\not\equiv j\pmod n,\omega_n^i\ne\omega_n^j,\forall i\equiv j\pmod n,\omega_n^i=\omega_n^j$
  • $\omega_n^k=\cos{\frac{2k\pi}{n}}+i\sin{\frac{2k\pi}{n}}$
  • $\omega_n^0=\omega_n^n=1$
  • $\omega_{rn}^{rk}=\omega_n^k$
  • $\omega_n^{k+\frac{n}{2}}=-\omega_n^k,\omega_n^{k+n}=\omega_n^k$
  • $\omega_n^i*\omega_n^j=\omega_n^{i+j}$ （相乘等于辐角相加）

前置知识：小性质

我们明确一个性质（在拉格朗日插值中也用到了该性质）：

  • 任意 $n+1$ 个不同的点（可以含复数）可以唯一确定一个 $n$ 次多项式（或者称其为 $n$ 次函数）

证明：

把每个点带人列得 $n+1$ 个 $n+1$ 元（因为下标从 $0$ 到 $n$ ）一次方程，明显可解，则每一项的系数唯一确定，原多项式确定

快速傅里叶正变换

有了以上性质，我们可以把一个 $n$ 次多项式用 $n+1$ 个点表示（也叫函数的点表示法），则答案推演如下：
$$
\begin{align}
&A(x)=a_0+a_1x+a_2x^2+…+a_nx^n\\
\text{可表示为}&A:{(x_1,A(x_1)),(x_2,A(x_2)),…,(x_{n+1},A(x_{n+1}))}\\
\text{同理}&B:{(x_1,B(x_1)),(x_2,B(x_2)),…,(x_{n+1},B(x_{n+1}))}\\
\text{则}C=A*&B:{(x_1,A(x_1)B(x_1)),(x_2,A(x_2)B(x_2)),…,(x_{n+1},A(x_{n+1})B(x_{n+1}))}
\end{align}
$$
我们发现在点表示法下求 $A*B$ 是 $O(n)$ 的，那么问题其实就变成了如何快速的实现点表示法和系数表示法的互相转换

我们观察性质，任意两个字是关键——我们可否通过取一些特殊的点来使求解变得简单呢？当然是可以的，FFT通过取复数域上的单位根来加上运算，也就是说，我们取 $\omega_{n+1}^0\sim\omega_{n+1}^n$

那么FFT如何利用这些点来将系数表示法转换为点表示法呢？先变形：
$$
\begin{align}
A(x)
&=a_0+a_1x+a_2x^2+…+a_nx^n\\
\text{分奇数项和偶数项，令}A_1(x)
&=a_0+a_2x+a_4x^2+a_6x^3+…\\
A_2(x)
&=a_1+a_3x+a_5x^2+a_7x^3+…\\
\text{明显，}A_1,A_2&\text{都是}\lfloor\frac{n}{2}\rfloor\text{次多项式}\\
\text{则}A(x)
&=A_1(x^2)+xA_2(x^2)\\
\text{遍历}k\in[0,\frac{n-1}{2}]\text{有}A(\omega_{n+1}^k)
&=A_1(\omega_{n+1}^{2k})+\omega_{n+1}^kA_2(\omega_{n+1}^{2k})\\
&=A_1(\omega_\frac{n+1}{2}^k)+\omega_{n+1}^kA_2(\omega_\frac{n+1}{2}^k)\\
\text{同样，有}A(\omega_{n+1}^{k+\frac{n+1}{2}})
&=A_1(\omega_{n+1}^{2k+n+1})+\omega_{n+1}^{k+\frac{n+1}{2}}A_2(\omega_{n+1}^{2k+n+1})\\
&=A_1(\omega_{n+1}^{2k})-\omega_{n+1}^{k}A_2(\omega_{n+1}^{2k})\\
&=A_1(\omega_\frac{n+1}{2}^k)-\omega_{n+1}^{k}A_2(\omega_\frac{n+1}{2}^k)\\
\text{我们发现只要我们求出}
&k\in[0,\frac{n-1}{2}]\text{时的所有}A_1(\omega_\frac{n+1}{2}^k)\text{和}\omega_{n+1}^{k}A_2(\omega_\frac{n+1}{2}^k)\\
\text{就可以计算出}
&k\in[0，n]\text{时的所有}A(\omega_{n+1}^k)
\end{align}
$$
由此，可以每次把区间分半，将系数多项式转换为点表示法，时间复杂度为 $O(n\log{n})$

快速傅里叶逆变换

现在已经解决了正变换，我们来看逆变换：
$$
\text{已知}A:{(\omega_{n+1}^k,A(\omega_{n+1}^k)),k\in[0,n]}\\
\text{设}A(x)=a_0+a_1x+a_2x^2+…+a_nx^n,y_k=A(\omega_{n+1}^k)\\
\text{则有}a_k(n+1)=\sum_{i=0}^{n}y_i(\omega_{n+1}^{-k})^i
$$
证明如下：

$$
\begin{align}
\sum_{i = 0} ^ {n} y_i (\omega_{n + 1} ^ {- k}) ^ i
&=\sum_{i=0}^{n} A(\omega_{n+1}^i) (\omega_{n+1}^{-k}) ^ i\\
&=\sum_{i=0}^{n} (\sum_{j=0}^{n} a_j (\omega_{n+1} ^ i ) ^ j ) (\omega_{n+1}^{-k}) ^ i\\
&=\sum_{i=0}^{n}(\sum_{j=0}^{n} a_j (\omega_{n+1}^j) ^ i (\omega_{n+1}^{-k}) ^ i)\\
&=\sum_{i=0}^{n}\sum_{j=0}^{n} a_j (\omega_{n+1}^{j-k}) ^ i\\
&=\sum_{j=0}^{n}\sum_{i=0}^{n} a_j (\omega_{n+1}^{j-k}) ^ i\\
&=\sum_{j=0}^{n}a_j (\sum_{i=0}^{n} (\omega_{n+1}^{j-k}) ^ i)\\
&\text{令}S(x)=\sum_{j=0}^{n}x^i\\
&\text{则} S(\omega_{n+1}^k)=\omega_{n+1}^0+\omega_{n+1}^k+\omega_{n+1}^{2k}+…+\omega_{n+1}^{nk}\\
&\omega_{n+1}^k S(\omega_{n+1}^k) =\omega_{n+1}^k+\omega_{n+1}^{2k}+\omega_{n+1}^{3k}+…+\omega_{n+1}^{(n+1)k}\\
\text{又}
&\because \omega_{n+1}^{(n+1)k}= \omega_{n+1}^0=1\\
&\therefore S(\omega_{n+1}^k)=\omega_{n+1}^k S(\omega_{n+1}^k)\\
&\therefore (1-\omega_{n+1}^k) S(\omega_{n+1}^k)=0\\
&\text{若}k=0\text{，即}1- \omega_{n+1}^k=0\\
&\text{则} S(\omega_{n+1}^k) = S(1) = n+1\\
&\text{若}k\ne0\text{，即} 1-\omega_{n+1}^k\ne0\\
&\text{则} S(\omega_{n+1}^k)=0\\
\text{总上所述} S(\omega_{n+1}^k)
&=[k==0] (n+1)\\
\text{故}\sum_{i=0}^{n} y_i (\omega_{n+1}^{-k})^i
&=\sum_{j=0}^{n} a_j S(\omega_{n+1}^{j-k})\\
&=\sum_{j=0}^{n} a_j [j==k] (n+1)\\
&=a_k(n+1)\\
\end{align}
$$

那么现在，有了 $a_k(n+1)=\sum_{i=0}^{n}y_i(\omega_{n+1}^{-k})^i$ ，不妨令 $A’(x)=\sum_{i=0}^{n}y_ix^i$ ，则 $a_k(n+1)=A’(\omega_{n+1}^{-k})$

我们只需要快速求出 $A’(\omega_{n+1}^{0})\sim A’(\omega_{n+1}^{-n})$ ——这正好就是快速傅里叶正变换！

递归化迭代

由于用递归实现FFT常数过大，我们考虑用迭代的方式实现FFT（其实常数也挺大的），观察下面的图：

迭代

计算每一个数时都要用到下方被横线连着的几个数，找找规律找的到个鬼，我们发现下面的每一项都是上面的数的二进制翻转，如 $1=(001)_2$ 对应最下方的 $4=(100)_2$ ，$6=(110)_2$ 对应最下方的 $3=(011)2$ ，不妨设 $i$ 二进制翻转后为 $r_i$ ，则有：
$$
i = (r{\frac{i}{2}} >> 1) {\Large|} (i & 1) << (bit - 1)
$$

为了好算，我们保证项数为 $2$ 的整次幂（不足就补）

代码

模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include<bits/stdc++.h>
using namespace std;
const int N=3000000+5; //注意N要大于二倍n 
const double PI=acos(-1);
struct Complex{ //定义复数 
	double a,b;
	Complex make_C(const double _a,const double _b)const{
		Complex res;
		res.a=_a,res.b=_b;
		return res;
	}
	Complex operator+(const Complex &_t)const{
		return make_C(a+_t.a,b+_t.b);
	}
	Complex operator-(const Complex &_t)const{
		return make_C(a-_t.a,b-_t.b);
	}
	Complex operator*(const Complex &_t)const{
		return make_C(a*_t.a-b*_t.b,a*_t.b+b*_t.a);
	}
}a[N],b[N];
int r[N],bit,tot;
void fft(Complex x[],int inv){
	for(int i=0;i<tot;++i)
		if(i<r[i]) swap(x[i],x[r[i]]);
	Complex w1,wk,a1,a2;
	for(int mid=1;mid<tot;mid<<=1){
		w1=w1.make_C(cos(PI/mid),inv*sin(PI/mid)); ; //由于cos正负相同,不必乘inv 
		for(int i=0;i<tot;i+=(mid<<1)){
			wk=wk.make_C(1,0);
			for(int j=0;j<mid;++j,wk=wk*w1){
				a1=x[i+j],a2=wk*x[i+j+mid];
				x[i+j]=a1+a2,x[i+j+mid]=a1-a2;
			}
		}
	}
}
int main(){
	int n,m; //建议将n,m定义为局部变量,防止与tot混淆 
	scanf("%d%d",&n,&m);
	for(int i=0;i<=n;++i) scanf("%lf",&a[i].a);
	for(int i=0;i<=m;++i) scanf("%lf",&b[i].a);
	while((1<<bit)<n+m+1) ++bit;
	tot=1<<bit;
	for(int i=0;i<tot;++i) r[i]=(r[i>>1]>>1)|((i&1)<<(bit-1)); 
	fft(a,1),fft(b,1);
	for(int i=0;i<tot;++i) a[i]=a[i]*b[i];
	fft(a,-1);
	for(int i=0;i<=n+m;++i) printf("%d ",(int)(a[i].a/tot+0.5)); //加0.5来四舍五入 
	return 0;
}

应用

FFT的题一般都转化成两个多项式（函数）的乘积，是来看一道题：

A*B

题目要求我们求一个高精乘高精，若直接求，显然 $O(n^2)$ ，考虑FFT优化：
$$
\begin{align}
A
&={a_{n-1} a_{n-2} …a_0}\\
B
&={b_{n-1} b_{n-2} …b_0}\\
\text{不妨设} f_A(x)
&=a_{n-1} x^{n-1} + a_{n-2} x^{n-2} +…+ a_0x^0\\
f_B(x)
&=b_{n-1} x^{n-1} + b_{n-2} x^{n-2} +…+ b_0x^0\\
\text{则} Ans
&=A* B\\
\end{align}
$$
那么问题就转化为求函数 $f_C=f_A*f_B$ 答案就是 $f_C$ 的系数

用FFT求 $f_C$ 时间复杂度 $O(n\log{n})$

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include<bits/stdc++.h>
using namespace std;
const int N=3000000+5;
const double PI=acos(-1);
struct Complex{
	double a,b;
	Complex make_C(const double _a,const double _b)const{
		Complex res;
		res.a=_a,res.b=_b;
		return res;
	}
	Complex operator+(const Complex &_t)const{
		return make_C(a+_t.a,b+_t.b);
	}
	Complex operator-(const Complex &_t)const{
		return make_C(a-_t.a,b-_t.b);
	}
	Complex operator*(const Complex &_t)const{
		return make_C(a*_t.a-b*_t.b,a*_t.b+b*_t.a);
	}
}a[N],b[N];
char s1[N],s2[N];
int ans[N];
int r[N],bit=0,tot=0;
void fft(Complex x[],int inv){
	for(int i=0;i<tot;++i)
		if(i<r[i]) swap(x[i],x[r[i]]);
	Complex w1,wk,a1,a2;
	for(int mid=1;mid<tot;mid<<=1){
		w1=w1.make_C(cos(PI/mid),inv*sin(PI/mid));
		for(int i=0;i<tot;i+=(mid<<1)){
			wk=wk.make_C(1,0);
			for(int j=0;j<mid;++j,wk=wk*w1){
				a1=x[i+j],a2=wk*x[i+j+mid];
				x[i+j]=a1+a2,x[i+j+mid]=a1-a2;
			}
		}
	}
}
int main(){
	int n,m;
	scanf("%s%s",s1,s2);
	n=strlen(s1)-1,m=strlen(s2)-1;
	for(int i=0;i<=n;++i) a[i].a=s1[n-i]-'0';
	for(int i=0;i<=m;++i) b[i].a=s2[m-i]-'0';
	while((1<<bit)<n+m+1) ++bit;
	tot=1<<bit;
	for(int i=0;i<tot;++i)
		r[i]=(r[i>>1]>>1)|((i&1)<<(bit-1));
	fft(a,1),fft(b,1);
	for(int i=0;i<tot;++i) a[i]=a[i]*b[i];
	fft(a,-1);
	int k=0;
	for(int i=0,_t=0;i<tot||_t;++i){
		_t+=a[i].a/tot+0.5;
		ans[k++]=_t%10;
		_t/=10;
	}
	while(k>1&&ans[k-1]==0) --k;
	for(int i=k-1;i>=0;--i) printf("%d",ans[i]);
	return 0;
}